Đề thi vào 10 Toán Tỉnh Vĩnh Phúc năm 2023-2024

Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t (c ế ó l i ờ gi i ả ) S Ở GIÁO D C Ụ VÀ ĐÀO T O Ạ VĨNH PHÚC KỲ THI TUY N Ể SINH VÀO L P Ớ 10 THPT NĂM H C Ọ 2023- 2024 ĐỀ CHÍNH TH C Ứ ĐỀ THI MÔN: TOÁN Th i
ờ gian làm bài: 120 phút (không k ể th i ờ gian phát đ ) ề I. PH N Ầ TR C Ắ NGHI M Ệ (2,0 đi m) ể Viết vào t gi
ờ ấy thi đáp án đúng mà em ch n ọ (Ví d :
ụ Câu 1 nếu ch n
ọ A là đúng thì vi t ế Câu 1: A). Câu 1. Biểu th c
ứ 120  6x có nghĩa khi A. x 1  20. B. x 12  0. C. x  20. D. x  20. Cấu 2. Hàm s ố y (
 m  2023)x  2024 (v i ớ m là tham s ) đ ố ng ồ bi n t ế rên R A. m  2023. B. m 2024.  C. m 2  023. D. m  2024. x  x Câu 3. Phư ng ơ trình 2
3x  7x  4 0  có hai nghi m ệ x , x . 1 2 Khi đó 1 2 bằng 7 1 4 1 .  . . . A. 3 B. 3 C. 3 D. 3
Câu 4. Cho tam giác ABC vuông tại , A biết rằng đ dà ộ i các cạnh AB 6  cm, AC 8  cm. Bán kính đư ng t ờ ròn ngoại ti p ế ABC bằng A. 10 cm. B. 5 2 cm. C. 5 cm. D. 10 cm. II. PH N Ầ T LU Ự N Ậ (8,0 đi m) ể 3  x  2 y 5   Câu 5. (1,0 đi m). ể Giải h ph ệ ư ng t ơ
rình x  3y 9   x x 1 x  1 A   Câu 6 (1,0 đi m). ể Cho biểu th c ứ x  1 x 1 (v i ớ x 0  ; x 1  ). a) Rút g n ọ bi u t ể h c ứ . A b) Tìm tất c c ả ác giá trị nguyên c a
ủ x để A nhận giá trị nguyên. 2 2 Câu 7 (2,0 đi m). ể Cho phư ng t ơ
rình x  (2m 1)x  m  1 0  (1) v i ớ m là tham s . ố a) Giải phư ng t ơ rình (1) khi m 5  . b) Tìm tất c c ả ác giá trị c a ủ tham s ố m để phư ng ơ trình (1) có hai nghi m ệ x , x 1 2 th a ỏ mãn đi u ề ki n: ệ 2 2
(x  2mx  m )(x 1) 4  . 1 2 Câu 8 (1,0 đi m). ể M t
ộ hãng taxi công nghệ cao có giá cư c ớ (giá ti n khá ề ch hàng ph i ả tr c ả ho m i ỗ km) đư c ợ tính theo các m c ứ sau: M c ứ 1: Giá m c ở a
ử cho 1 km đầu tiên là 2000 đ ng; ồ M c
ứ 2: Từ trên 1 km đ n 25 km ế ; M c ứ 3: Từ trên 25 km; M i
ọ thắc mắc vui lòng xin liên h h
ệ otline: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t (c ế ó l i ờ gi i ả )
Biết anh A đi 32 km phải trả ti n t ề axi là 479500 đ ng
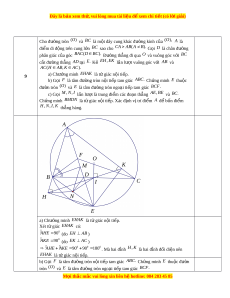
ồ còn chị B đi 41 km phải trả 592000 đ ng. ồ H i ỏ giá cư c ớ c a ủ hãng taxi m ở c ứ 2 và m c ứ 3 là bao nhiêu? N u khá ế ch hàng đi 24 km thì ph i ả tr t ả axi bao nhiêu ti n? ề Câu 9 (2,5 đi m). ể Cho đư ng t ờ
ròn (O) và BC là m t
ộ dây cung khác đư ng kí ờ nh c a
ủ (O), A là điểm di đ ng t ộ rên cung l n
ớ BC sao cho CA  AB(A B). G i
ọ D là chân đư ng ờ phân giác c a
ủ góc BAC(D  BC). Đư ng t ờ
hẳng đi qua O và vuông góc v i ớ BC cắt đư ng
ờ thẳng AD tại E. K
ẻ EH , EK lần lư t ợ vuông góc v i
ớ AB và AC(H  AB, K  AC). a) Chư ng
ớ minh EHAK là tứ giác n i ộ ti p. ế b) G i
ọ F là tâm đư ng t ờ ròn n i ộ ti p
ế tam giác ABC. Ch ng ứ minh E thu c ộ đư n t
ờ ròn (O) và E là tâm đư ng ờ tròn ngoại ti p ế tam giác BCF. c) G i
ọ M , N, I lần lượt là trung đi m
ể các đoạn thẳng AE, BE và BC. Ch ng
ứ minh BMDN là tứ giác n i ộ tiếp. Xác đ nh v ị ị trí đi m ể A để b n ố đi m
ể H , N, I, K thẳng hàng. Câu 10 (0,5 đi m). ể Cho các s t ố h c ự a, , b c sao cho phư ng ơ trình 2
ax  bx  c  2023 0  nhận x 1  là nghi m ệ . Tìm giá trị nh nh ỏ ất c a ủ bi u ể th c ứ . 2 2 2 2 2 2
P  3a  2ab 3b  5b  6bc 5c  6c  8ca  6a .
---------------------H t-------------------- ế Thí sinh không đư c ợ s d ử ng ụ tài li u. ệ Cán b c ộ oi thi không gi i ả thích gì thêm H v
ọ à tên thí sinh……………………………………………S báo dnh-------------------------- ố S Ở GIÁO D C Ụ VÀ ĐÀO T O Ạ VĨNH PHÚC ĐÁP ÁN Đ Ề THI VÀO L P Ớ 10 THPT NĂM H C Ọ 2023-2024 ĐỀ THI MÔN: TOÁN I. PH N Ầ TR C Ắ NGHI M Ệ (2,0 đi m). M ể i ỗ câu tr l ả i
ờ đúng cho 0,5 đi m ể Câu 1 2 3 4 Đáp án B A D C II. PH N Ầ T LU Ự N Ậ (8,0 đi m) ể Câu N i ộ dung Đi m ể 3  x  2 y 5   Giải h ph ệ ư ng t ơ
rình x  3y 9   5 3  x  2 y 5  x 9   3y x 9   3y x 9   3y x 3          x   3y 9  
3(9  3y)  2y 5  11y  22 y  2 y  2     Vậy hệ phư ng
ơ trình có nghiệm là (x, y) (3  ;  2) M i
ọ thắc mắc vui lòng xin liên h h
ệ otline: 084 283 45 85
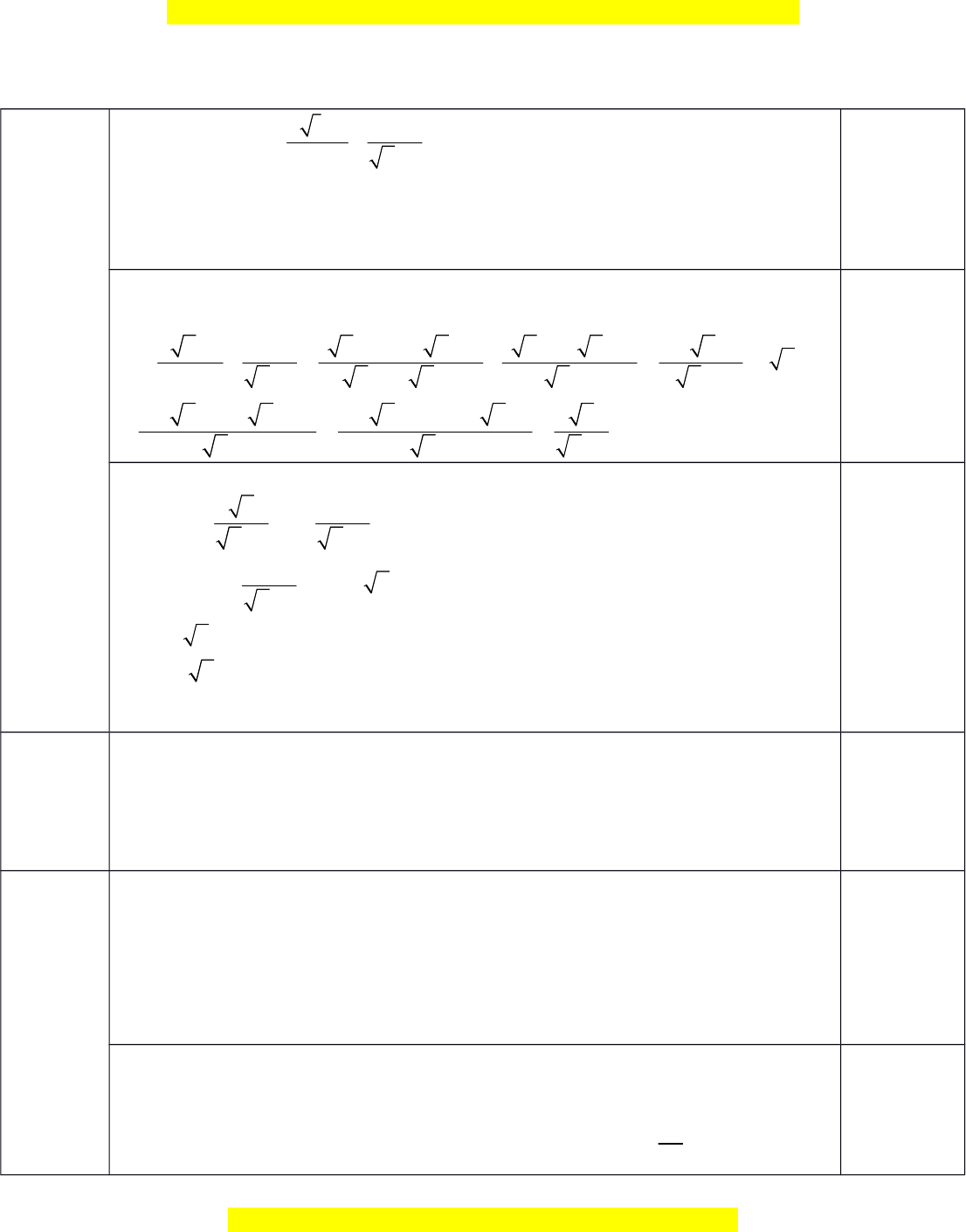
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t (c ế ó l i ờ gi i ả ) x 1 1 x  1 A   Cho biểu th c ứ x  1 x 1 (v i ớ x 0  ; x 1  ). a) Rút g n ọ bi u t ể h c ứ . A b) Tìm tất c c ả ác giá trị nguyên c a
ủ x để A nhận giá trị nguyên. a) Rút g n ọ bi u t ể h c ứ . A x x 1 x  1 ( x 1)(x 
x 1) ( x  1)( x 1) x  x 1 A       ( x  1) x  1 x 1
( x  1)( x 1) x 1 x  1 6 2
x  x 1 ( x  1) x 
x 1 x  2 x  1 x    x  1 x  1 x  1 b) Tìm tất c c ả ác giá trị nguyên c a
ủ x để A nhận giá trị nguyên. x 1 A  1   Ta có: x  1 x  1 1  Z  x  1  1;  1
Để A Z thì x  1 (1) Ư   + Nếu x  1 1   x 4  (th a ỏ mãn ĐK).
+ Nếu x  1  1  x 0  (th a ỏ mãn ĐK). x  0; 4 Vậy 
 thì A có giá trị nguyên. 2 2 Cho phư ng t ơ
rình x  (2m 1)x  m  1 0  (1) v i ớ m là tham s . ố a) Giải phư ng t ơ rình (1) khi m 5.  b) Tìm tất c c ả ác giá trị c a ủ tham s ố m để phư ng ơ trình (1) có hai nghi m ệ x , x 1 2 2 2 th a ỏ mãn điều ki n
ệ : (x  2mx  m )(x 1) 4  . 1 2 7 a) Giải phư ng t ơ rình (1) khi m 5.  Khi m 5  , ta có phư ng ơ trình: 2
x  11x  24 0  2 Ta có  (   11)  4.24 25   0 Phư ng t ơ rình có hai nghi m ệ phân biệt: x 3  ; x 8 1 2  S  3;8 Vậy tập nghiệm c a ủ phư ng ơ trình là:   b) Tìm tất c c ả ác giá trị c a ủ tham s ố m để phư ng ơ trình (1) có hai nghi m ệ x , x 1 2 2 2 Ta có  (
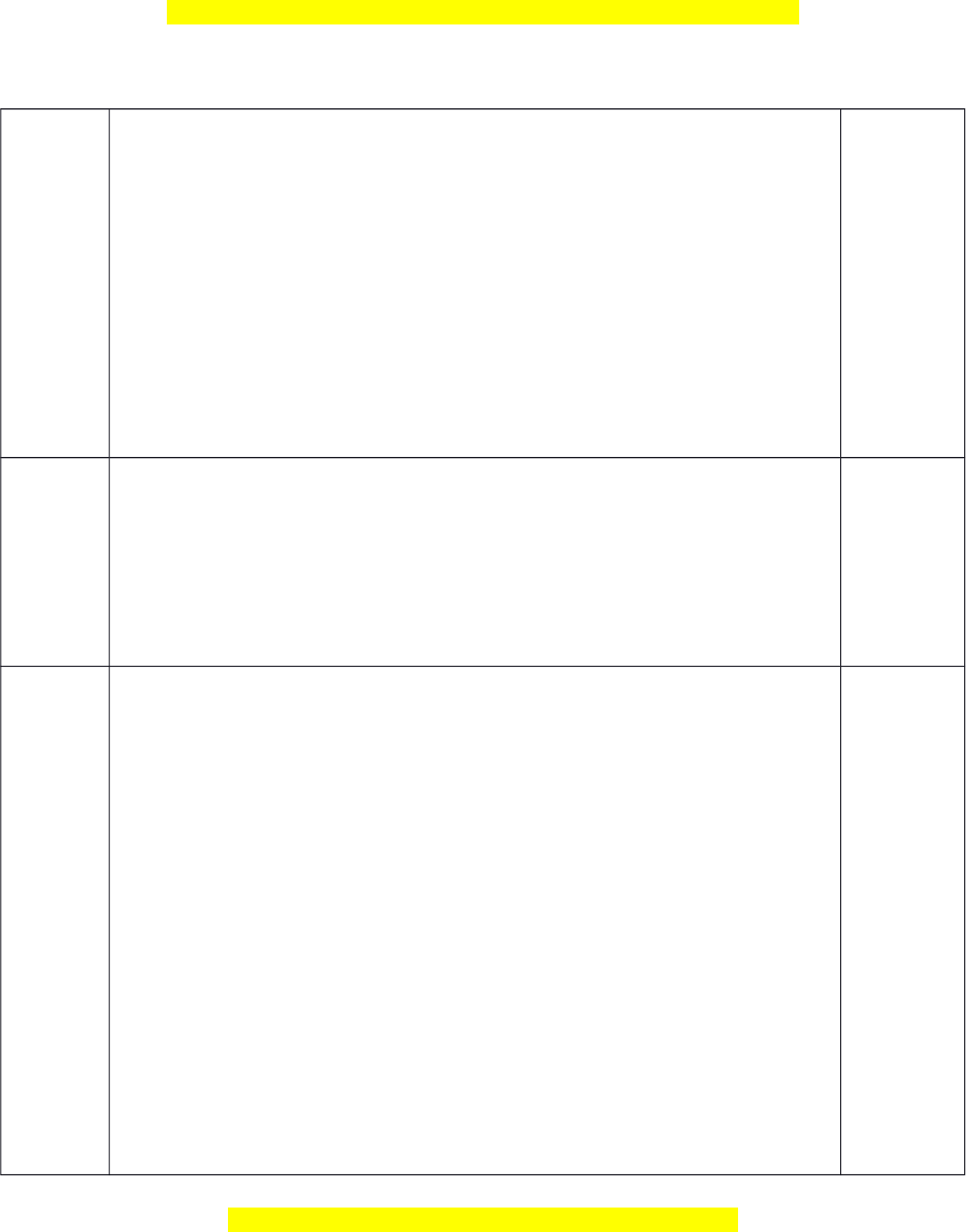
 2m 1)  4(m  1) 4  m  5 4 0 4m 5 0 m         Để phư ng ơ trình có hai nghi m ệ thì 5 M i
ọ thắc mắc vui lòng xin liên h h
ệ otline: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t (c ế ó l i ờ gi i ả ) x  x 2  m 1  1 2  2 x .x m   1 Theo h t
ệ hức Vi-et, ta có:  1 2 Vì x1 là nghi m ệ c a ủ phư ng ơ trình (1) nên ta có: 2 2 2 2
x  (2m 1)x  m  1 0
  x  2mx  m x 1 1 1 1 1 1 2 2 2 2
Thay x  2mx  m x 1
(x  2mx  m )(x 1) 4  . 1 1 1 vào 1 2 Ta có
(x 1)(x 1) 4
  x x  x  x 3 1 2 1 2 1 2  suy ra  m 1  (t / m) 2 2
m  1 2m 1 3
  m  2m  3 0    m 3  (ktm)  Vậy v i ớ m 1  thì phư ng t ơ rình (1) có hai nghi m ệ x , x 1 2 thảo mãn điều ki n ệ 2 2
(x  2mx  m )(x 1) 4  . 1 2 M t
ộ hãng taxi công nghệ cao có giá cư c ớ (giá ti n khá ề ch hàng ph i ả tr c ả ho m i ỗ km) đư c ợ tính theo các m c ứ sau: M c ứ 1: Giá m c ở a
ử cho 1 km đầu tiên là 2000 đ ng; ồ M c
ứ 2: Từ trên 1 km đ n 25 km ế ; 8 M c ứ 3: Từ trên 25 km;
Biết anh A đi 32 km phải trả ti n t ề axi là 479500 đ ng ồ còn chị B đi 41 km phải trả 592000 đ ng. ồ H i ỏ giá cư c ớ c a ủ hãng taxi m ở c ứ 2 và m c ứ 3 là bao nhiêu? N u khá ế
ch hàng đi 24 km thì phải trả taxi bao nhiêu ti n? ề G i ọ giá cư c ớ c a ủ hãng taxi m ở c ứ 2 là x đ ng (Đ ồ K x  0 ) G i ọ giá cư c ớ c a ủ hãng taxi m ở c ứ 3 là y đ ng ồ (ĐK y  0 )
Anh A: Trả tiền ở m c
ứ 2 là (25  1)x 24x (đ ng) ồ Trả tiền m
ở ức 3 là (32  25) y 7  y (đ ng) ồ Theo bài ra ta có phư ng ơ tringh:
2000  24x  7 y 47950 
0  24x  7 y 4595  00 (1) Chị B: Trả tiền m
ở ức 2 là (25  1)x 24x (đ ng) ồ Trả tiền m
ở ức 3 là (41 25) y 1  6 y (đ ng) ồ Theo bài ra ta có phư ng ơ tringh:
2000  24x 16y 592000   24x 16 y 572000  (2) T (1) và ừ (2) ta có h ph ệ ư ng ơ trình: 24x  7 y 4  59500 24x  7 y 4  59500 x 1  5500     24x 16y 572000 9 y 112500     y 1  2500    (th a ỏ mãn ĐK) Vậy: Giá ti n c ề a ủ hãng taxi m ở ức 2 là 15500 đ ng ồ Giá tiền c a ủ hãng taxi ở m c ứ 3 là 125000 đ ng ồ
Nên khách hàng đi 24 km thì phải tr s ả t ố i n l
ề à: 20000  23.15500 37650  0 đ ng. ồ M i
ọ thắc mắc vui lòng xin liên h h
ệ otline: 084 283 45 85