Bộ 7 đề thi cuối kì 2 Toán 10 TP Hồ Chí Minh có đáp án

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM ĐỀ KIỂM TRA HỌC KỲ II
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI Năm học: 2022 – 2023
Môn Toán – Khối: 10 Thời gian: 90 phút
(Không kể thời gian phát đề)
Họ tên học sinh: …………………………………………………….. SBD:………………………
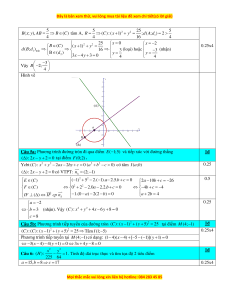
Câu 1: (1,0 điểm) Giải phương trình: 2
3x − 2x +1 = x +1
Câu 2: (1,0 điểm) Tìm m sao cho 2
f (x) = (m − 2)x + (1− 2m)x + m  0, x   . Câu 3: (3,0 điểm)
a) Trong nhà sách hiện đang có 9 mẫu sổ lưu niệm, 7 mẫu thiệp chúc và 5 mẫu túi giấy. Hỏi bạn An có
bao nhiêu cách chọn một phần quà gồm một sổ lưu niệm, một thiệp chúc và một túi giấy? (1,0 điểm)
b) Sử dụng nhị thức Newton, khai triển 4
(3x + 4) và tìm số hạng chứa 3
x trong khai triển. (1,0 điểm)
c) Tổ Toán trường Nguyễn Thị Minh Khai dự định tổ chức một buổi ngoại khóa và mỗi lớp sẽ chọn 5
học sinh tham gia. Lớp 10T có tất cả 30 học sinh, trong đó có 20 nữ. Tính xác suất để cả 5 học sinh
được chọn đi ngoại khóa đều là nam? (1,0 điểm)
Câu 4: (2,0 điểm) Trong mặt phẳng Oxy , cho đường thẳng (d : 4x + 3y − 6 = 0 và điểm ( A 1 − ;0) . 1 )
a) Viết phương trình tổng quát của đường thẳng (d đi qua A và vuông góc với (d ) . (1,0 điểm) 2 ) 1 5
b) Tìm tọa độ điểm B sao cho AB =
và khoảng cách từ B đến (d ) là lớn nhất. (1,0 điểm) 4 1
Câu 5: (2,0 điểm) Trong mặt phẳng Oxy ,
a) Viết phương trình đường tròn đi qua điểm E( 1
− ;5) và tiếp xúc với đường thẳng () : 2x − y + 2 = 0 tại
điểm F(0;2) . (1,0 điểm)
b) Viết phương trình tiếp tuyến của đường tròn 2 2
(C) : (x −1) + ( y + 5) = 25 tại điểm M (4; 1 − ) (1,0 điểm) 2 2 x y
Câu 6: (1,0 điểm): Trong mặt phẳng Oxy , cho hyperbol (H ) : −
=1. Tính độ dài trục thực và tìm tọa 225 64
độ 2 tiêu điểm của (H ) . HẾT


ĐÁP ÁN & BIỂU ĐIỂM (Toán 10)
Câu 1 : Giải phương trình 2
3x − 2x +1 = x +1 1đ 2 2
Pt  3x − 2x +1 = (x +1) 0.25 2
 2x − 4x = 0  x = 2 hay x = 0 0.50
Thử lại: Phương trình có nghiệm là x = 0 hay x = 2 0.25
Câu 2: Tìm m sao cho 2
f (x) = (m − 2)x + (1− 2m)x + m  0, x   1đ 2 0.25
. m = 2 : f (x) = 3
− x + 2  0  x  (không thỏa ycbt) 3 m  2  0.50 m − 2  0 m  2  . m  2 :      1 − 2
(1− 2m) − 4m(m − 2)  0 1  + 4m  0 m   4 1 − 0.25 Vậy m  thỏa ycbt 4
Câu 3a: Trong nhà sách hiện đang có 9 mẫu sổ lưu niệm, 7 mẫu thiệp chúc và 5 mẫu túi 1đ
giấy. Hỏi bạn An có bao nhiêu cách chọn một phần quà gồm một sổ lưu niệm, một thiệp chúc và một túi giấy?
Bước 1: Chọn một sổ lưu niệm: có 9 cách. 0.25x4
Bước 2: Chọn một thiệp chúc: có 7 cách.
Bước 3: Chọn một túi giấy: có 5 cách.
 Có 9.7.5 = 315 cách (theo quy tắc nhân).
Câu 3b: Khai triển 4
(3x + 2) . Tìm số hạng chứa 3 x 1đ 4 4 4 3 3 2 2 2 1 3 0 4
(3x + 2) = C (3x) + C (3x) .2 + C (3x) .2 + C (3 ) x .2 + C 2 0.5 4 4 4 4 4 4 3 2
= 81x + 216x + 216x + 96x +16 0.25 Số hạng chứa 3 x là 3 216x 0.25
Câu 3c: Tổ Toán trường Nguyễn Thị Minh Khai dự định tổ chức một buổi ngoại khóa và 1đ
mỗi lớp sẽ chọn 5 học sinh tham gia. Lớp 10T có tất cả 30 học sinh, trong đó có 20 nữ.
Tính xác suất để cả 5 học sinh được chọn đi ngoại khóa đều là nam? 5 ( n )  = C =142506 0.5 30
Gọi A là biến cố 5 học sinh được chọn đi ngoại khóa đều là nam: 5 ( n ) A = C = 252 0.25 10 n( ) A 252 2 0.25 P( ) A = = = n() 142506 1131
Câu 4a: Phương trình tổng quát của đường thẳng (d đi qua A và vuông góc với (d ) 1đ 2 ) 1
(d ) : 3x − 4 y + m = 0 0.25 2 ( A 1
− ;0)(d )  3.( 1
− ) − 4.0 + m = 0  m = 3 0.5 2
Vậy (d ) : 3x − 4 y + 3 = 0 0.25 2 5 1đ
Câu 4b: Tìm tọa độ điểm B sao cho AB =
và khoảng cách từ B đến (d ) là lớn nhất. 4 1

5 5 25 5 B( ; x y), AB =
 B (C) tâm A, 2 2 R =
 (C) : (x +1) + y = ; d ( ; A d ) = 2  4 1 4 16 4  25 x = 0  = − 2 2  x 2 B  (C) (x +1) + y =   0.25x4 d ( ; B d )     16   (loại) hoặc  − (nhận) 1 min 3 3 B  (d )  y = y = 2 3
 x −4y +3 = 0   4  4  −3  Vậy B −2;    4  Hình vẽ
Câu 5a: Phương trình đường tròn đi qua điểm E( 1
− ;5) và tiếp xúc với đường thẳng 1đ
() : 2x − y + 2 = 0 tại điểm F (0; 2) . Ycbt 2 2 2 2
(C) : x + y − 2ax − 2by + c = 0 (a + b − c  0) có tâm I ( ; a b) 0.25
() : 2x − y + 2 = 0 có VTPT: n = (2; 1 − )  2 2 E (C) ( 1 − ) + 5 − 2.( 1
− ).a− 2.5.b + c = 0
2a −10b + c = 2 − 6 0.5    2 2 F (C)
 0 + 2 − 2.0a − 2.2.b + c = 0   4 − b + c = 4 −    ⊥   1
− .(0 − a) − 2(2 − b) = 0 a + 2b = 4 IF ( ) IF cp n     a = 2 − 0.25   b  = 3 (nhận). Vậy 2 2
(C) : x + y + 4x − 6 y + 8 = 0 c = 8 
Câu 5b: Phương trình tiếp tuyến của đường tròn 2 2
(C) : (x −1) + ( y + 5) = 25 tại điểm M (4; 1 − ) 1đ 2 2
(C) : (C) : (x −1) + ( y + 5) = 25  Tâm I (1; 5 − ) 0.25x4
Phương trình tiếp tuyến tại M (4; 1
− ) có dạng: (1− 4)(x − 4) +[ 5 − − ( 1 − )](y +1) = 0  3
− (x − 4) − 4(y +1) = 0  3x + 4y −8 = 0 2 2 x y 1đ Câu 6: (H ) : −
=1. Tính độ dài trục thực và tìm tọa độ 2 tiêu điểm 225 64
a = 15,b = 8  c = 17 0.25x4