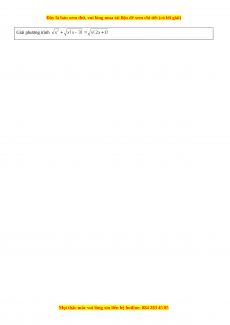Chuyên đề 1. PHƯƠNG TRÌNH
I. TÓM TẮT LÝ THUYẾT
Đối với phương trình vô tỷ (tức là phương trình có chứa ẩn trong dấu căn), điều cần lưu ý nhất là tính
không thuận nghịch của các phép toán. Chẳng hạn nếu trong một phương trình nào đó, bạn thay
(với và là các biểu thức nào đó của ) bởi
thì tập xác định của phương trình rất có thể bị mở rộng, bởi vì chỉ xác dịnh khi và trong khi xác định ngay cả khi và
. Vậy bạn chỉ thu được một phương trình hệ quả. Ngược lại, nếu thay thế bởi
thì tập xác định có thể bị thu hẹp lại, do đó bạn rất dễ bị bỏ sót nghiệm. Điều đó cảnh báo rằng khi thực
hiện một phép tính về căn thức, để biến đổi một phương trình thì nói chung bạn không được phương
trình tương đương. Để tránh các sai sót kiểu như thế, người ta dùng một trong các cách sau:
Cách 1: Nếu chắc chắn phép biến đổi chỉ cho phương trình hệ quả thì ở bước cuối cùng, ta dùng phép
thử trực tiếp vào phương trình để loại bỏ nghiệm ngoại lai. Ví dụ: Giải phương trình Giải:
Phương trình đã cho, suy ra:
Thử trực tiếp vào phương trình, ta thấy thỏa mãn, còn không thỏa mãn.
Vậy phương trình có nghiệm là: .
Cách 2: Ghi nhớ tập xác định của phương trình và các điều kiện cần thiết khác trước khi biến đổi
phương trình. Nếu phép biến đổi dẫn đến phương trình hệ quả thì nghiệm ngoại lai chính là các giá trị
của ẩn không nằm trong tập xác định hoặc không thỏa mãn các điều kiện đã nêu. Đôi khi, chính tập xác
định và các điều kiện ấy sẽ đem lại những gợi ý hữu ích cho bạn trong quá trình giải phương trình. Ví dụ:
Giải phương trình
Giải: Điều kiện + Xét , thỏa mãn phương trình + Xét
phương trình đã cho tương đương với
(vô nghiệm vì giá trị của căn thức không thể bằng một số âm) + Xét
, phương trình đã cho tương đương với Nhận thấy không thỏa mãn nên bị loại.
Vậy phương trình đã cho có nghiệm: Cách 3
Chú ý đến các điều kiện xác định của phương trình, các điều kiện để thực hiện các phép biến đổi đồng
nhất hay biến đổi tương đương phương trình và đặt các điều kiện đó cùng với phương trình trong một hệ
hỗn hợp (cả phương trình và bất phương trình). Hệ này sẽ tương đương với phương trình đã cho.
Nhưng dù theo cách nào thì bạn cũng phải chú ý đến các điều kiện nảy sinh trong quá trình biến đổi
phương trình, đặc biệt là sự thay đổi tập xác định của phương trình. Điều đó sẽ giúp bạn có những quyết
định đúng đắn khi giải phương trình.
Dưới đây là một số đồng nhất thức có điều kiện thường gặp: Đồng nhất thức Điều kiện * DẠNG 1: và
Phương pháp: Sử dụng
công thức của định nghĩa và
căn bậc hai số học và và và
và
Chú ý: Sau khi tìm nghiệm của bài toán xong, chúng ta nên thử lại nghiệm để tránh sai sót trong tính toán. Ví dụ 1: Giải phương trình: Giải:
Phương trình tương đương với
Vậy phương trình có nghiệm là: Ví dụ 2: Giải phương trình: Giải:
Phương trình tương đương với
Vậy phương trình có nghiệm là:
Bộ chinh phục luyện thi vào 10 môn Toán có đáp án
1.1 K
563 lượt tải
130.000 ₫
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Bộ tài liệu bao gồm: 2 tài liệu lẻ (mua theo bộ tiết kiệm đến 50%)
- Tailieugiaovien.com.vn giới thiệu bộ tài liệu chinh phục luyện thi vào 10 môn Toán bao gồm: Phần 1: Các chuyên đề hay và khó; Phần 2: Bộ 30 đề thi có đáp án mới nhất nhằm giúp Giáo viên có thêm tài liệu tham khảo đề luyện thi Toán ôn luyện vào 10.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1126 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Ôn vào 10
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Chuyên đề 1. PHƯƠNG TRÌNH
I. TÓM TẮT LÝ THUYẾT
Đối với phương trình vô tỷ (tức là phương trình có chứa ẩn trong dấu căn), điều cần lưu ý nhất là tính
không thuận nghịch của các phép toán. Chẳng hạn nếu trong một phương trình nào đó, bạn thay
(với và là các biểu thức nào đó của ) bởi thì tập xác định của phương trình rất có thể bị
mở rộng, bởi vì chỉ xác dịnh khi và trong khi xác định ngay cả khi
và . Vậy bạn chỉ thu được một phương trình hệ quả. Ngược lại, nếu thay thế bởi
thì tập xác định có thể bị thu hẹp lại, do đó bạn rất dễ bị bỏ sót nghiệm. Điều đó cảnh báo rằng khi thực
hiện một phép tính về căn thức, để biến đổi một phương trình thì nói chung bạn không được phương
trình tương đương. Để tránh các sai sót kiểu như thế, người ta dùng một trong các cách sau:
Cách 1: Nếu chắc chắn phép biến đổi chỉ cho phương trình hệ quả thì ở bước cuối cùng, ta dùng phép
thử trực tiếp vào phương trình để loại bỏ nghiệm ngoại lai.
Ví dụ:
Giải phương trình
Giải:
Phương trình đã cho, suy ra:
Thử trực tiếp vào phương trình, ta thấy thỏa mãn, còn không thỏa mãn.
Vậy phương trình có nghiệm là: .
Cách 2: Ghi nhớ tập xác định của phương trình và các điều kiện cần thiết khác trước khi biến đổi
phương trình. Nếu phép biến đổi dẫn đến phương trình hệ quả thì nghiệm ngoại lai chính là các giá trị
của ẩn không nằm trong tập xác định hoặc không thỏa mãn các điều kiện đã nêu. Đôi khi, chính tập xác
định và các điều kiện ấy sẽ đem lại những gợi ý hữu ích cho bạn trong quá trình giải phương trình.
Ví dụ:
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Giải phương trình
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Giải:
Điều kiện
+ Xét , thỏa mãn phương trình
+ Xét phương trình đã cho tương đương với
(vô nghiệm vì giá trị của căn thức không thể
bằng một số âm)
+ Xét , phương trình đã cho tương đương với
Nhận thấy không thỏa mãn nên bị loại.
Vậy phương trình đã cho có nghiệm:
Cách 3
Chú ý đến các điều kiện xác định của phương trình, các điều kiện để thực hiện các phép biến đổi đồng
nhất hay biến đổi tương đương phương trình và đặt các điều kiện đó cùng với phương trình trong một hệ
hỗn hợp (cả phương trình và bất phương trình). Hệ này sẽ tương đương với phương trình đã cho.
Nhưng dù theo cách nào thì bạn cũng phải chú ý đến các điều kiện nảy sinh trong quá trình biến đổi
phương trình, đặc biệt là sự thay đổi tập xác định của phương trình. Điều đó sẽ giúp bạn có những quyết
định đúng đắn khi giải phương trình.
Dưới đây là một số đồng nhất thức có điều kiện thường gặp:
* DẠNG 1:
Phương pháp: Sử dụng công thức của định nghĩa
căn bậc hai số học
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đồng nhất thức Điều kiện
và
và
và
và
và
và

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Chú ý: Sau khi tìm nghiệm của bài toán xong, chúng ta nên thử lại nghiệm để tránh sai sót trong tính
toán.
Ví dụ 1:
Giải phương trình:
Giải:
Phương trình tương đương với
Vậy phương trình có nghiệm là:
Ví dụ 2:
Giải phương trình:
Giải:
Phương trình tương đương với
Vậy phương trình có nghiệm là:
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
BÀI TẬP TƯƠNG TỰ
1) Giải phương trình:
Đáp số:
2) Giải phương trình:
Đáp số:
3) Giải phương trình:
Đáp số:
4) Giải phương trình:
Đáp số:
* DẠNG 2:
Phương pháp: Phương trình tương đương với
Ví dụ :
Giải phương trình:
Giải:
Phương trình tương đương với
BÀI TẬP TƯƠNG TỰ:
1) Giải phương trình:
Đáp số:
2) Giải phương trình:
Đáp số:
3) Giải phương trình:
Đáp số:
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85