xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải) Đây là bản CHƯƠNG 1 HÌNH 9
Bài 1:.Để đo chiều cao CD của một cái tháp (C là chân tháp, D là đỉnh tháp), một
người chọn 2 điểm A,B sao cho C,A,B thẳng hàng và quan sát tháp, kết quả quan sát
như hình vẽ, và A cách B 24m. Tính chiều cao của tháp. Bài giải:
Áp dụng các công thức lượng giác trong tam giác CAD,CBD:
Vậy chiều cao của tháp xấp xỉ 74,3m
Bài 2:. Hai học sinh A (vị trí A) và học sinh B (vị trí
B) đang đứng ở mặt đất cách nhau 100m cùng nhìn
máy bay trực thăng ở vị trí C. Biết góc nâng ở vị trí A
là 55 độ, góc nâng ở vị trí B là 48 độ. Hãy tính độ cao
của máy bay so với mặt đất. Bài giải:
Áp dụng các công thức lượng giác trong tam giác CHA,CHB:
Vậy độ cao của máy bay so với mặt đất xấp xỉ 52,86m.
Bài 3: Một người thợ sử dụng thước ngắm có góc vuông để đo chiều cao của một cây
dừa, với các kích thước đo được như hình bên. Khoảng cách từ vị trí gốc cây đến vị trí
chân của người thợ là 4,8m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của
người ngắm là 1,6m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của
cây đó là bao nhiêu? (làm tròn đến mét).
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải) Đây là bản Bài giải:
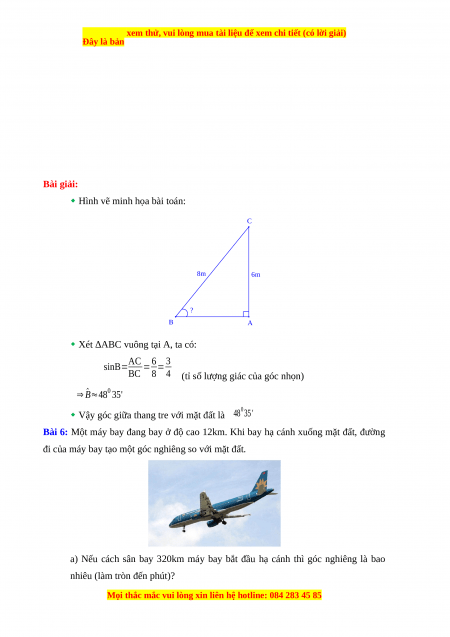
Hình vẽ minh họa bài toán: C B D 1,6m 4,8m A H Xét tứ giác ABDH có:
^A= ^B= ^H=900 (hình vẽ)
⇒ Tứ giác ABDH là hình chữ nhật (dấu hiệu nhận biết) ⇒ BA=DH=1,6m ; BD=AH=4,8m
Xét ∆ADC vuông tại D và DB là đường cao, ta có:
DB2=BA .BC (hệ thức lượng) DB2 4,82 ⇒ BC= = =14,4m BA 1,6 ⇒ AC=AB+ BC=1,6+14,4=16m
Vậy chiều cao của cây dừa là 16m
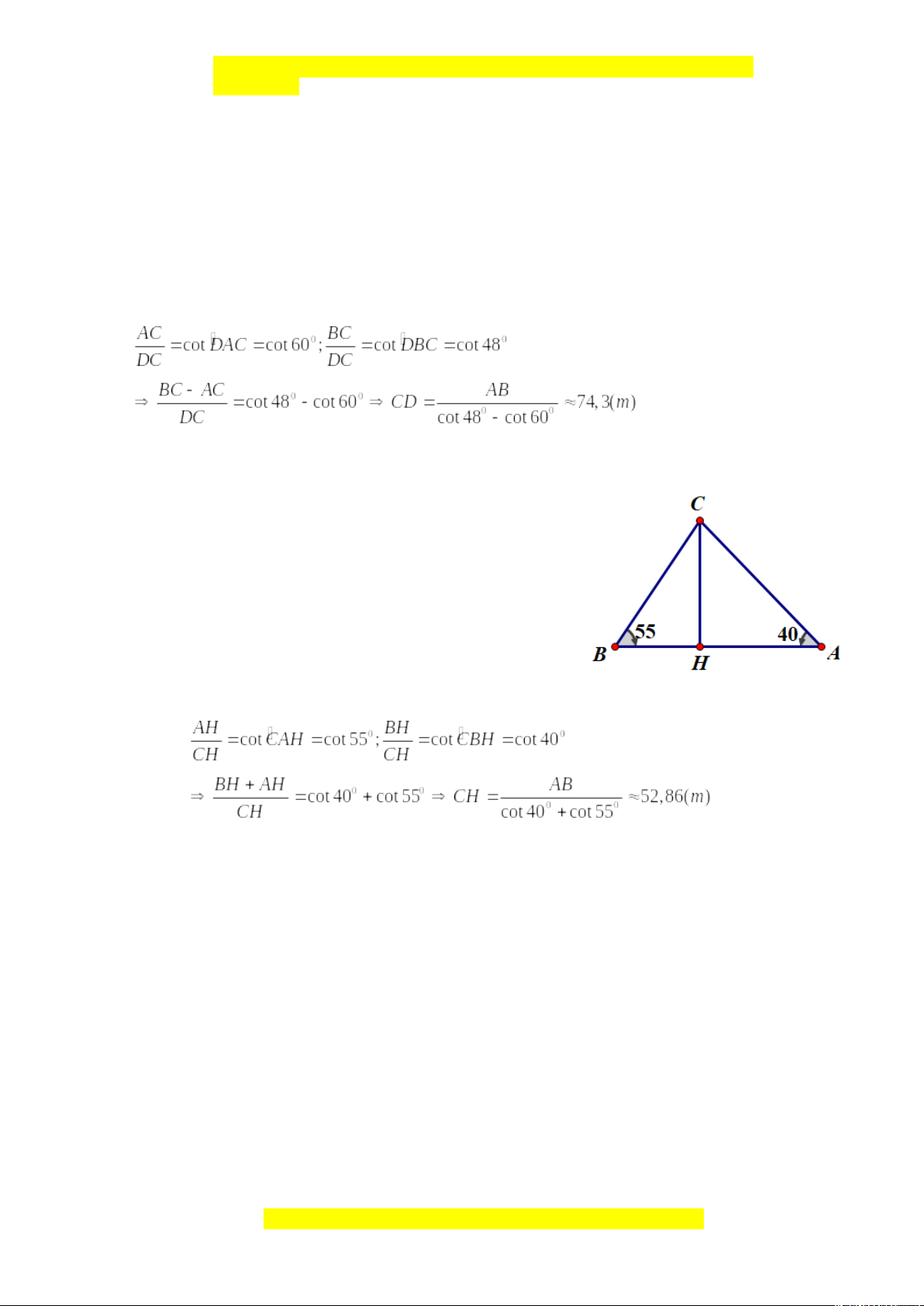
Bài 4: Muốn tính khoảng cách từ điểm A đến điểm B nằm bên kia bờ sông, ông Việt
vạch từ A đường vuông góc với AB. Trên đường vuông góc này lấy một đoạn thẳng
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải) Đây là bản
AC = 30m, rồi vạch CD vuông góc với phương BC cắt AB tại D (xem hình vẽ). Đo
AD = 20m, từ đó ông Việt tính được khoảng cách từ A đến B. Em hãy tính độ dài AB và số đo góc ACB. Bài giải:
Xét ∆BCD vuông tại C và CA là đường cao, ta có:
AB.AD=AC2 (hệ thức lượng) AC2 302 ⇒ AB= = =45m AD 20
Xét ∆ABC vuông tại A, ta có: AB 45 tanACB= = =1,5 AC 30
(tỉ số lượng giác của góc nhọn)
⇒ A ^C B≈56018'
Vậy tính độ dài AB = 45m và số đo góc ACB là 56018’
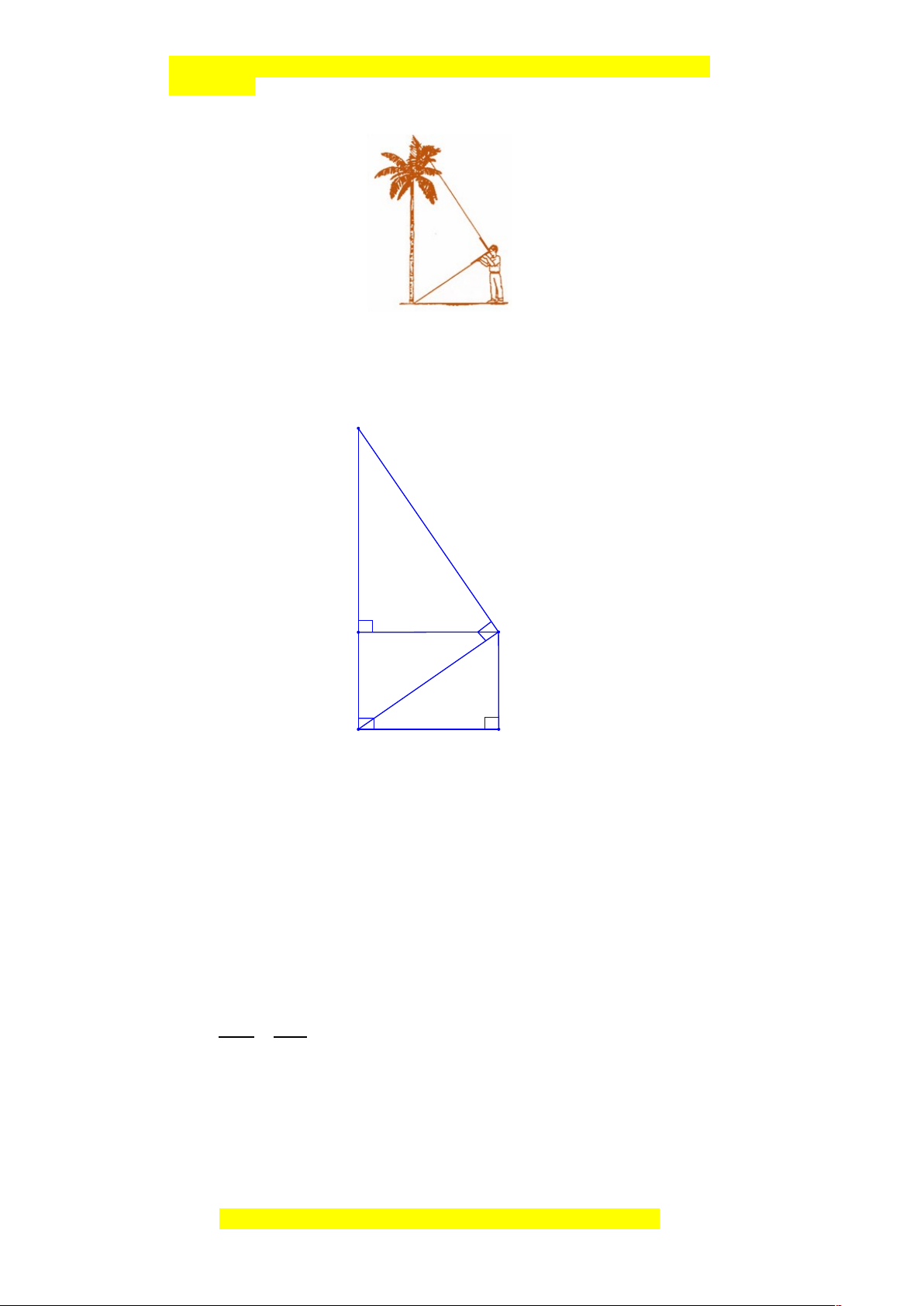
Bài 5: Một cây cau có chiều cao 6m. Để hái một buồn cau xuống, phải đặt thang tre
sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với mặt đất là bao nhiêu,
biết chiếc thang dài 8m (làm tròn đến phút)
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải) Đây là bản Bài giải:
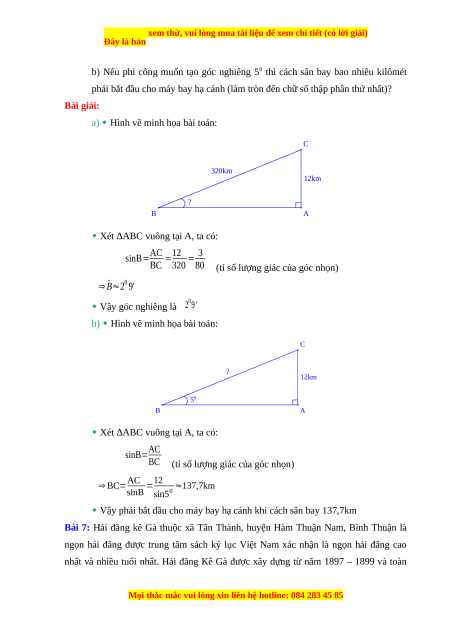
Hình vẽ minh họa bài toán: C 8m 6m ? B A
Xét ∆ABC vuông tại A, ta có: AC 6 3 sinB= = = BC
8 4 (tỉ số lượng giác của góc nhọn) ⇒ ^B≈480 35'
Vậy góc giữa thang tre với mặt đất là 48035'
Bài 6: Một máy bay đang bay ở độ cao 12km. Khi bay hạ cánh xuống mặt đất, đường
đi của máy bay tạo một góc nghiêng so với mặt đất.
a) Nếu cách sân bay 320km máy bay bắt đầu hạ cánh thì góc nghiêng là bao
nhiêu (làm tròn đến phút)?
Các bài toán thực tế ôn vào 10 Hình học (tặng kèm)
1 K
521 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Bộ tài liệu bao gồm: 4 tài liệu lẻ (mua theo bộ tiết kiệm đến 50%)
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu cách giải các bài toán thực tế ôn vào lớp 10 môn Toán Hình học mới nhất năm 2022 - 2023 nhằm giúp Giáo viên có thêm tài liệu tham khảo ôn vào 10 môn Toán.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1042 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Ôn vào 10
Xem thêmTài liệu bộ mới nhất
Đây là bản
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
CHƯƠNG 1 HÌNH 9
Bài 1:.Để đo chiều cao CD của một cái tháp (C là chân tháp, D là đỉnh tháp), một
người chọn 2 điểm A,B sao cho C,A,B thẳng hàng và quan sát tháp, kết quả quan sát
như hình vẽ, và A cách B 24m. Tính chiều cao của tháp.
Bài giải:
Áp dụng các công thức lượng giác trong tam giác CAD,CBD:
Vậy chiều cao của tháp xấp xỉ 74,3m
Bài 2:. Hai học sinh A (vị trí A) và học sinh B (vị trí
B) đang đứng ở mặt đất cách nhau 100m cùng nhìn
máy bay trực thăng ở vị trí C. Biết góc nâng ở vị trí A
là 55 độ, góc nâng ở vị trí B là 48 độ. Hãy tính độ cao
của máy bay so với mặt đất.
Bài giải:
Áp dụng các công thức lượng giác trong tam
giác CHA,CHB:
Vậy độ cao của máy bay so với mặt đất xấp xỉ 52,86m.
Bài 3: Một người thợ sử dụng thước ngắm có góc vuông để đo chiều cao của một cây
dừa, với các kích thước đo được như hình bên. Khoảng cách từ vị trí gốc cây đến vị trí
chân của người thợ là 4,8m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của
người ngắm là 1,6m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của
cây đó là bao nhiêu? (làm tròn đến mét).
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Bài giải:
Hình vẽ minh họa bài toán:
1,6m
4,8m
H
D
C
B
A
Xét tứ giác ABDH có:
^
A=
^
B=
^
H=90
0
(hình vẽ)
⇒
Tứ giác ABDH là hình chữ nhật (dấu hiệu nhận biết)
⇒ BA=DH=1,6m
;
BD=AH=4,8m
Xét ∆ADC vuông tại D và DB là đường cao, ta có:
DB
2
=BA .BC
(hệ thức lượng)
⇒ BC=
DB
2
BA
=
4,8
2
1,6
= 14,4m
⇒ AC=AB+BC=1,6+14,4=16m
Vậy chiều cao của cây dừa là 16m
Bài 4: Muốn tính khoảng cách từ điểm A đến điểm B nằm bên kia bờ sông, ông Việt
vạch từ A đường vuông góc với AB. Trên đường vuông góc này lấy một đoạn thẳng
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
AC = 30m, rồi vạch CD vuông góc với phương BC cắt AB tại D (xem hình vẽ). Đo
AD = 20m, từ đó ông Việt tính được khoảng cách từ A đến B. Em hãy tính độ dài AB
và số đo góc ACB.
Bài giải:
Xét ∆BCD vuông tại C và CA là đường cao, ta có:
AB.AD=AC
2
(hệ thức lượng)
⇒ AB=
AC
2
AD
=
30
2
20
=45m
Xét ∆ABC vuông tại A, ta có:
tanACB=
AB
AC
=
45
30
=1,5
(tỉ số lượng giác của góc nhọn)
⇒ A
^
C B≈56
0
18'
Vậy tính độ dài AB = 45m và số đo góc ACB là 56
0
18’
Bài 5: Một cây cau có chiều cao 6m. Để hái một buồn cau xuống, phải đặt thang tre
sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với mặt đất là bao nhiêu,
biết chiếc thang dài 8m (làm tròn đến phút)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Bài giải:
Hình vẽ minh họa bài toán:
?
8m
6m
C
B
A
Xét ∆ABC vuông tại A, ta có:
sinB=
AC
BC
=
6
8
=
3
4
(tỉ số lượng giác của góc nhọn)
⇒
^
B≈48
0
35'
Vậy góc giữa thang tre với mặt đất là
48
0
35'
Bài 6: Một máy bay đang bay ở độ cao 12km. Khi bay hạ cánh xuống mặt đất, đường
đi của máy bay tạo một góc nghiêng so với mặt đất.
a) Nếu cách sân bay 320km máy bay bắt đầu hạ cánh thì góc nghiêng là bao
nhiêu (làm tròn đến phút)?
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản
xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
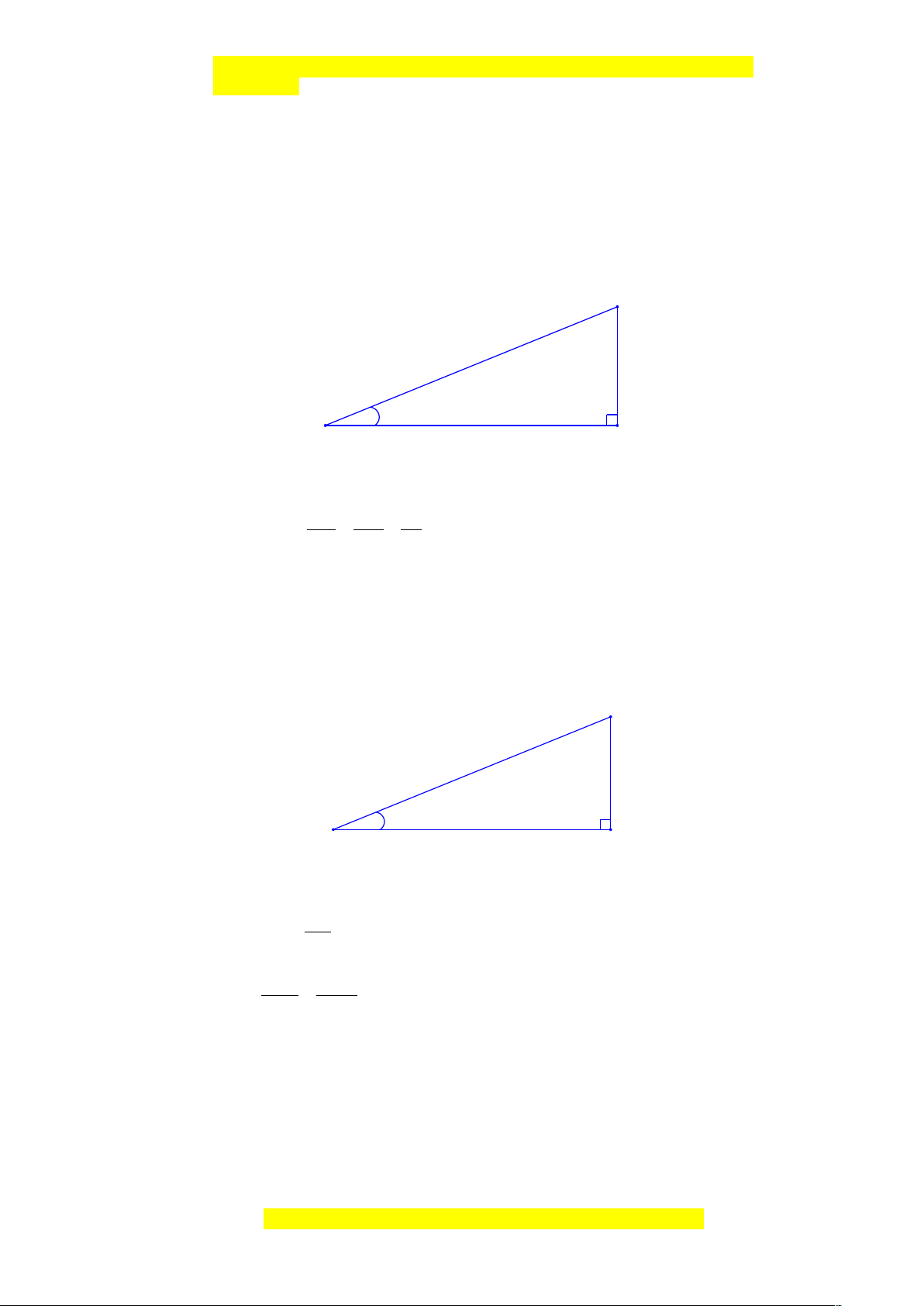
b) Nếu phi công muốn tạo góc nghiêng 5
0
thì cách sân bay bao nhiêu kilômét
phải bắt đầu cho máy bay hạ cánh (làm tròn đến chữ số thập phân thứ nhất)?
Bài giải:
a) Hình vẽ minh họa bài toán:
?
320km
12km
C
A
B
Xét ∆ABC vuông tại A, ta có:
sinB=
AC
BC
=
12
320
=
3
80
(tỉ số lượng giác của góc nhọn)
⇒
^
B≈2
0
9'
Vậy góc nghiêng là
2
0
9'
b) Hình vẽ minh họa bài toán:
B
A
C
12km
?
5
0
Xét ∆ABC vuông tại A, ta có:
sinB=
AC
BC
(tỉ số lượng giác của góc nhọn)
⇒ BC=
AC
sinB
=
12
sin5
0
≈ 137,7km
Vậy phải bắt đầu cho máy bay hạ cánh khi cách sân bay 137,7km
Bài 7: Hải đăng kê Gà thuộc xã Tân Thành, huyện Hàm Thuận Nam, Bình Thuận là
ngọn hải đăng được trung tâm sách kỷ lục Việt Nam xác nhận là ngọn hải đăng cao
nhất và nhiều tuổi nhất. Hải đăng Kê Gà được xây dựng từ năm 1897 – 1899 và toàn
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85