Chuyên đề dạy thêm Toán 9 Chân trời sáng tạo Chương 10

CHƯƠNG X. CAC HINH KHÔI TRONG THƯC TIÊN BÀI 1. HINH TRỤ
A. KIẾN THỨC CƠ BẢN CẦN NẮM I. HINH TRỤ 1. Nhận biết hình trụ
Nhận xét: Hình được tạo ra khi quay một hình chữ nhật một vòng xung quanh đường thẳng cố định chứa
một cạnh của nó là hình trụ.
Với hình trụ như ở Hình 3, ta có:
- Hình tròn tâm D bán kính DA và hình tròn tâm C bán kính CB là hai mặt đáy; hai mặt đáy của hình trụ
bằng nhau và nằm trong hai mặt phẳng song song;
- Độ dài cạnh DA được gọi là bán kính đáy;
- Độ dài cạnh CD được gọi là chiều cao;
- Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB được gọi là một đường sinh; độ
dài đường sinh bằng chiều cao của hình trụ. 2. Tạo lập hình trụ
Ví dụ 1. Đối với hình trụ sau, hãy chỉ ra:
a) Một đường sinh của hình trụ;
b) Độ dài bán kính đáy, chiều cao của hình trụ. Lời giải
a) Đoạn thẳng AB là một đường sinh của hình trụ đó.
b) Độ dài bán kính đáy, chiều cao của hình trụ đó lần lượt là 2 cm,4 cm .
II. DIỆN TÍCH XUNG QUANH CỦA HINH TRỤ
Diện tích xung quanh của hình trụ bằng tích của chu vi đáy với chiều cao: S  C h  rh trong đó S xq 2 , xq
là diện tích xung quanh, C là chu vi đáy, r là bán kính đáy, h là chiều cao của hình trụ.
Ví dụ 2. Cho một hình trụ có bán kính đáy là 4 cm và chiều cao là 10 cm . Hỏi diện tích xung quanh của
hình trụ đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)? Lời giải
Diện tích xung quanh của hình trụ đó là: S        xq  2 2 4 10 80 251,33 cm 
Chú ý: Tổng của diện tích xung quanh và diện tích hai đáy của hình trụ gọi là diện tích toàn phần của hình trụ.
Diện tích toàn phần S của hình trụ được tính theo công thức: 2
S  rh  r , trong đó r là bán kính tp 2 2 tp
đáy và h là chiều cao của hình trụ.
III. THỂ TÍCH CỦA HINH TRỤ
Thể tích của hình trụ bằng tích của diện tích đáy với chiều cao: 2
V  S.h  r h trong đó V là thể tích, S
là diện tích đáy, r là bán kính đáy, h là chiều cao của hình trụ.
Ví dụ 3. Một khối gỗ có dạng hình trụ với bán kính đáy khoảng 13 cm và chiều cao khoảng 43 cm (Hình
9). Hỏi thể tích của khối gỗ đó là bao nhiêu centimét khối (làm tròn kết quả đến hàng phần trăm)? Lời giải
Thể tích của khối gỗ đó là: 2 V         3 13 43 7267 22829,95 cm  B. CAC DẠNG TOAN
Dạng 1. Nhận dạng và tạo lập hình trụ
Câu 1: Trong các hình sau đây, hình nào là hình trụ?
Câu 2: Trong các vật thể ở các hình dưới đây, vật thể nào có dạng hình trụ?
Câu 3: Tạo lập hình trụ có bán kính đáy r  5cm và chiều cao h  8cm
Dạng 2. Tính bán kính đáy, đường cao, diện tích, thể tích của hình trụ 1. Phương pháp
Cho hình trụ có bán kính đáy r và chiều cao h .
 Diện tích xung quanh: S  rh xq 2
 Diện tích toàn phần: S  r h  r tp 2    Thể tích: 2 V  r h 2. Các ví dụ
Câu 1: Thay dấu “? ”bằng giá trị thích hợp và hoàn thành bảng sau: Bán kính đáy Chiều cao Diện tích xung Diện tích toàn Thể tích Hình trụ (cm) (cm) quanh (cm2) phần (cm2) (cm3) 3 7 ? ? ? 4 ? 20 ? ? ? 8 ? 18 ? ? 5 ? ? 150
Câu 2: Cho hình trụ có bán kính đáy bằng 5 dm . Biết rằng hình trụ đó có diện tích toàn phần gấp đôi
diện tích xung quanh. Tính chiều cao hình trụ.
Câu 3: Hỏi nếu tăng chiều cao của khối trụ lên 2 lần, bán kính của nó lên 3 lần thì thể tích của khối
trụ mới sẽ tăng bao nhiêu lần so với khối trụ ban đầu?
Câu 4: Cho hình chữ nhật ABCD có AB 1cm, AD  2 cm  . Gọi M , N lần lượt là trung điểm của
AD và BC . Quay hình chữ nhật đó xung quanh trục MN ta được một hình trụ như hình vẽ.
a) Tính diện tích toàn phần S của hình trụ đó. tp
b) Tính thể tích hình trụ đó.
Dạng 3. Ứng dụng của hình trụ trong thực tiễn 1. Phương pháp
Cho hình trụ có bán kính đáy r và chiều cao h .
 Diện tích xung quanh: S  rh xq 2
 Diện tích toàn phần: S  r h  r tp 2    Thể tích: 2 V  r h 2. Các ví dụ
Câu 1: Một khúc gỗ hình trụ có đường kính đáy bằng 1,2 m, chiều cao bằng bán kính đáy (như hình vẽ).
a) Tính diện tích xung quanh của khúc gỗ đó (làm tròn kết quả đến phần trăm). b) Với thành hiện tại, 3
1 m gỗ trên bán được 5 triệu đồng. Hãy tính giá thành khúc gỗ trên nếu đem đi bán.
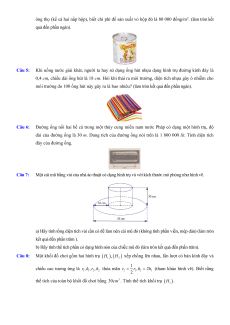
Câu 2: Một bồn nước inox Đại Thanh có dạng hình trụ với chiều cao 1,75 m và diện tích đáy là 0,32 m2.
a) Tính bán kính đáy của bồn nước inox Đại Thanh (làm tròn kết quả đến phần trăm).
b) Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn).
Câu 3: Người ta dự định làm dự định làm một chiếc bồn chứa dầu bằng sắt hình trụ có chiều cao
1,8 m, đường kính đáy 1,2 m. Hỏi chiếc bồn đó chứa đầy được bao nhiêu lít dầu, biết rằng
1 m3 = 1000 lít (Bỏ qua bề dày của bồn, lấy   3,14 )
Câu 4: Một doanh nghiệp sản xuất vỏ hộp sữa ông thọ dạng hình trụ, có chiều cao bằng 12 cm. Biết thể
tích của hộp là 192 cm3. Tính số tiền mà doanh nghiệp cần chi để sản xuất 10 000 vỏ hộp sữa