Chuyên đề dạy thêm Toán 9 Chương 4 Chân trời sáng tạo mới nhất

BÀI 1. TỈ SỐ LƯỢNG GIÁC GÓC NHỌN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. KHÁI NIỆM TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
Khái niệm sin, côsin, tang, côtang của góc nhọn 
Nhận xét. Trong Hình 4.4 , các tam giác vuông có cùng một góc nhọn  là đồng dạng với nhau. Vì vậy
các tỉ số giữa cạnh đối và cạnh huyền (cạnh kề và cạnh huyền), cạnh đối và cạnh kề (cạnh kề và cạnh đối)
của góc nhọn  là như nhau, cho dù độ dài các cạnh đối (các cạnh kề) của góc  và các cạnh huyền có
thể khác nhau với từng tam giác.
Cho góc nhọn  . Xét tam giác ABC vuông tại A có góc nhọn B bằng  . (H.4.5). Ta có:
- Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của  , kí hiệu sin .
- Tỉ số giữa cạnh kề và cạnh huyền gọi là côsin của  , kí hiệu cos .
- Tỉ số giửa cạnh đối và cạnh kề của góc  gọi là tang của  , kí hiệu tan  .
- Tỉ số giữa cạnh kề và cạnh đối của góc  gọi là côtang của  , kí hiệu cot . Chú ý. Ta có:   1 cot   . tan 
 sin,cos, tan,cot gọi là các tỉ số lượng giác của góc nhọn  . Chú ý:
sin, côsin của góc nhọn luôn dương và bé hơn 1 vì trong tam giác vuông, cạnh huyền dài nhất
Ví dụ 1. Cho tam giác ABC vuông tại A , có AB  3 cm, AC  4 cm(H.4.6) . Hãy tính các tỉ số lượng giác
sin  , cos , tan với ˆ   B . Lời giải
Xét ABC vuông tại , A B   .
Theo Định lí Pythagore, ta có: 2 2 2 2 2
BC  AC  AB  4  3  25 nên BC  5( cm).
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, ta có: AC 4 AB 3 AC 4 sin    ,cos   , tan   . BC 5 BC 5 AB 3
Chú ý: sin còn được viết là ˆ
sin B hay sin B . Tương tự cho cos, tan và cot  .
Giá trị lượng giác sin, côsin, tang, côtang của các góc 30, 45, 60 Ta có bảng sau:  30 45 60 sin 1 2 3 2 2 2 cos 3 2 1 2 2 2 tan 3 1 3 3 cot 3 1 3 . 3
Ví dụ 2. Cho tam giác ABC vuông tại A có C  30 và BC  a (H.4.8). Tính các cạnh AB, AC theo a . Lời giải AB 1 a Ta có sin C 
, suy ra AB  BC sinC  asin30 . Theo bảng trên, sin 30  nên AB  . BC 2 2 Tương tự AC a 3 , ta có cos C 
, suy ra AC  BC  cos C  a  cos 30  . BC 2
2. TỈ SỐ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU
a) Tỉ số lượng giác của hai góc phụ nhau
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Chú ý. Cho  và  là hai góc phụ nhau (H.4.9), khi đó
sin  cos  , cos  sin  , tan  cot  , cot   tan .
- Vẽ số đo, hai góc phụ nhau có thể coi là hai góc nhọn của một tam giác vuông.
Ví dụ 3. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 45 : sin 60 ,  cos 75 ,  sin 52 3  0 , tan80 ,  cot 82 .  Lời giải Ta có:
sin 60  cos90  60  cos30 ; 
cos 75  sin 90  75  sin15 ;  sin 52 3
 0  cos9052 3  0  cos37 3  0 ;
tan 80  cot 90 80  cot10 ; 
cot 82  tan 90 82  tan8 . 
3. SỬ DỤNG MÁY TÍNH CẦM TAY TÍNH TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
Chú ý: Về số đo góc, dưới đơn vị độ  còn có các đơn vị phút (") và giây (") với 1  60, 1  60 . 
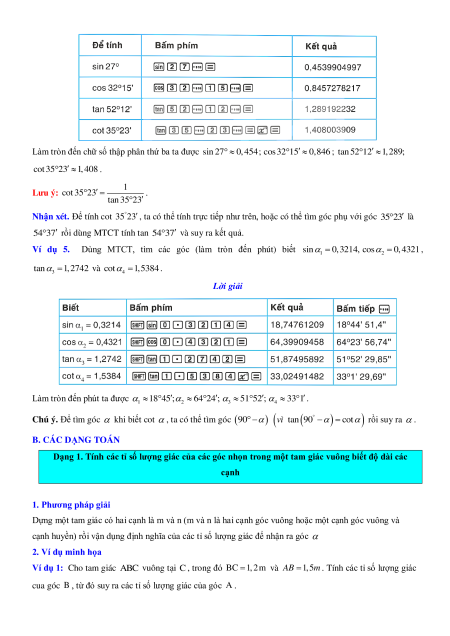
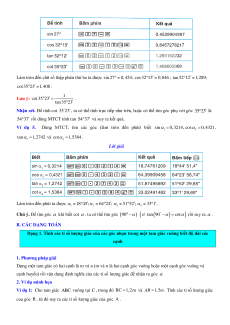
Ví dụ 4. 1  60, 1  60 . Dùng MTCT, tính sin 27 ,  cos32 1  5 , tan 52 1
 2 và cot 35 23 (làm tròn đến
chữ số thập phân thứ ba). Lời giải
Làm tròn đến chữ số thập phân thứ ba ta được sin 27  0, 454; cos32 1  5  0,846 ; tan 52 1  2 1,289; cot 35 2  3 1,408 . Lưu ý: 1 cot 35 23    . tan 35 23  
Nhận xét. Để tính cot 3523 , ta có thể tính trực tiếp như trên, hoặc có thể tìm góc phụ với góc 35 2  3 là 54 3
 7 rồi dùng MTCT tính tan 54 3
 7 và suy ra kết quả.
Ví dụ 5. Dùng MTCT, tìm các góc (làm tròn đến phút) biết sin  0,3214, cos  0, 4321 , 1 2
tan  1, 2742 và cot  1,5384 . 3 4 Lời giải
Làm tròn đến phút ta được  18 4  5 ;  64 2  4 ;   51 5  2 ;   33 1  . 1 2 3 4
Chú ý. Để tìm góc  khi biết cot  , ta có thể tìm góc 90   vì tan 90    cot  rồi suy ra  . B. CÁC DẠNG TOÁN
Dạng 1. Tính các tỉ số lượng giác của các góc nhọn trong một tam giác vuông biết độ dài các cạnh
1. Phương pháp giải
Dựng một tam giác có hai cạnh là m và n (m và n là hai cạnh góc vuông hoặc một cạnh góc vuông và
cạnh huyền) rồi vận dụng định nghĩa của các tỉ số lượng giác để nhận ra góc  2. Ví dụ minh họa
Ví dụ 1: Cho tam giác ABC vuông ta ̣i C , trong đó BC  1, 2 m và AB  1,5m . Tính các tỉ số lượng giác
cua góc B , từ đó suy ra các tỉ số lượng giác của góc A .