SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI BÌNH PHƯỚC
CẤP TỈNH LỚP 9 NĂM HỌC 2022 - 2023 MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài:150 phút (Không kể thời gian phát đề) Ngày thi: 18/03/2023
(Đề gồm có 01 trang) Câu 1: (5.0 điểm). − + − − 1. Cho biểu thức x 3 x 2 9 x 3 x 9 P = + − : 1−
2 − x 3+ x x + x − 6 x 9 −
a) Tìm điều kiện xác định và rút gọn biểu thức P .
b) Tính giá trị của biểu thức P khi x = 3 − 3− 13− 48 .
2. Cho x, y, z là ba số thực khác 0 , thoả mãn 1 1 1 + + = 0. x y z
Chứng minh rằng: yz zx xy + + = 3. 2 2 2 x y z Câu 2: (5.0 điểm).
1. Giải phương trình: 3x +1 − x + 3 +1− x = 0. 2 2 2xy x + y + = 1
2. Giải hệ phương trình: x + y . 2
x + y = x − y
3. Cho đường thẳng (d):mx+(m−1)y−2m+1= 0 (với m là tham số). Tìm điểm cố định
mà đường thẳng(d) luôn đi qua với mọi giá trị của m .
Câu 3: (5.0 điểm). Cho đường tròn ( ;
O R) và dây cung BC cố định (BC < 2R). Điểm A
di động trên đường tròn ( ;
O R) sao cho tam giác ABC nhọn. Kẻ đường cao AD và trực
tâm H của tam giác ABC .
a) Đường thẳng chứa phân giác ngoài của góc BHC cắt AB, AC lần lượt tại các điểm
M , N . Chứng minh tam giác AMN cân.
b) Các điểm E, F lần lượt là hình chiếu của D trên các đường thẳng BH,CH . Các
điểm P,Q lần lượt là hình chiếu của D trên các cạnh AB, AC . Chứng minh 4 điểm
P, E, F,Q thẳng hàng và OA ⊥ PQ .
c) Đường tròn ngoại tiếp tam giác AMN cắt đường phân giác trong của góc BAC tại
K . Chứng minh đường thẳng HK luôn đi qua một điểm cố định.
Câu 4: (2.0 điểm). Cho tam giác ABC cân tại A, điểm O là trung điểm của BC . Đường
tròn (O) tiếp xúc với các cạnh AB ,AC lần lượt tại E,F . Điểm H chạy trên cung nhỏ
EF của (O) , tiếp tuyến của đường tròn (O) tại H cắt ,
AB AC lần lượt tại M,N . Xác
định vị trí của điểm H để diện tích tam giác AMN đạt giá trị lớn nhất. Câu 5: (3.0 điểm).
1. Cho a,b,c là ba số thực dương, thoả mãn ab +bc + ca =1. Chứng minh rằng: 5 4 2 4 2 4 2
+ a b + b c + c a ≥ 2abc(a + b + c) . 9
2. Giải phương trình sau với nghiệm nguyên: 2 2
x + 2y + 3xy + 3x + 5y − 3 = 0 .
…………… Hết ……………
• Thí sinh không được sử dụng tài liệu.
• Giám thị không giải thích gì thêm.
HƯỚNG DẪN CHẤM KÌ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
NĂM HỌC 2022 – 2023 Môn: Toán - Lớp 9
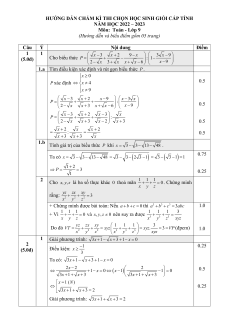
(Hướng dẫn và biểu điểm gồm 05 trang) Câu Ý Nội dung Điểm 1 1 x − x + − x x − (5.0đ) Cho biểu thức 3 2 9 3 9 P = + − : 1−
2 − x 3+ x x + x − 6 x 9 −
1.a Tìm điều kiện xác định và rút gọn biểu thức P . x ≥ 0
P xác định ⇔ x ≠ 4 0.5 x ≠ 9 x −3 x + 2
x − 9 x − 3 = + + : x P 2 − x
x + 3 x + x − 6 x 9 − 0.5 x −3 x + 2 x − 3 = + + : x P 2 x x 3 x 2 − + − x + 3 0.5 x + 2 + = : x x 2 = 0.5 x + 3 x + 3 x
1.b Tính giá trị của biểu thức P khi x = 3− 3− 13− 48 . Ta có 0.75
x = 3 − 3− 13− 48 = 3 − 3− (2 3 − ) 1 = 3 − ( 3 − ) 1 =1 1 2 P + ⇒ = = 3 1 0.25
2 Cho x, y,z là ba số thực khác 0 thoả mãn 1 1 1 + + = 0. Chứng minh x y z rằng: yz zx xy + + = 3 2 2 2 x y z
+ Chứng minh được bài toán: Nếu a + b + c = 0 thì 3 3 3
a + b + c = 3abc 1.0 + Vì 1 1 1
+ + = 0 và x, y, z ≠ 0 nên suy ra được 1 1 1 3 + + = x y z 3 3 3 x y z xyz Do đó yz zx xy 1 1 1 3 VT = + + = xyz + + = xyz. = 3 = VP (đpcm) 2 2 2 3 3 3 1.0 x y z x y z xyz
1 Giải phương trình: 3x +1− x +3 +1− x = 0 2 0.25 (5.0đ) Điều kiện: 1 x − ≥ 3
Ta có: 3x +1 − x + 3 +1− x = 0 2x − 2 x (x ) 2 1 0 1 1 ⇔ + − = ⇔ − − = 0.5 0 3x +1 + x + 3
3x +1 + x + 3 x = 1 (N) ⇔ 0.25
3x +1 + x + 3 = 2
Giải phương trình: 3x +1 + x + 3 = 2
⇒ 4x + 4 + 2 (3x +1)(x + 3) = 4 ⇔ (3x +1)(x + 3) = 2
− x (Đk: x ≤ 0 )
x = 5+ 2 7 (L) 2
⇒ x −10x − 3 = 0 ⇔ 0.75
x = 5− 2 7 (N)
Vậy phương trình có 2 nghiệm là x =1; x = 5− 2 7 . 1 2 0.25 2 2 2 2xy x + y + = 1 (1)
Giải hệ phương trình: x + y 2
x + y = x − y (2)
Điều kiện: x + y > 0. 0.25
Biến đổi phương trình (1): 2 2 2xy + + = ⇔ ( + )2 2 1 − 2 xy x y x y xy + −1 = 0 x + y x + y 0.25
Đặt x + y = S, xy = P (với 2
S ≥ 4P ), ta có phương trình: 2 2P S + − 2P −1 = 0 3
⇔ S + 2P − 2SP − S = 0 S S =1 0.5 2
⇔ S(S −1) − 2P(S −1) = 0 2
⇔ (S −1)(S + S − 2P) = 0 ⇔ 2
S + S − 2P = 0 +Với
x + y =1 thay vào (2) ta được: y = 1 = (1− y)2 0 2
− y ⇔ y − 3y = 0 ⇔ ⇒ ( ; x y)∈ ( { 1;0);( 2 − ;3)} y = 3 0.5 + Với 2
S + S − 2P = 0 ⇔ (x + y)2 + x + y − 2xy = 0 2 2
⇔ x + y + x + y = 0 (Loại, vì x + y > 0). 0.25
Vậy hệ phương trình đã cho có 2 nghiệm ( ;x y) là (1;0);( 2 − ;3) 0.25
3 Cho đường thẳng (d) : mx + (m −1)y − 2m +1= 0 (với m là tham số). Tìm
điểm cố định mà đường thẳng(d) luôn đi qua với mọi giá trị của m.
Gọi A(x y là điểm cố định mà đường thẳng (d) luôn đi qua với mọi A; A )
giá trị của m, ta có phương trình:
mx + m − y − m + = ⇔ x + y − m = y − có nghiệm m ∀ A ( 1) A 2 1 0 ( A A 2) A 1 0.5 x + y − = x = A A 2 0 A 1 ⇔ ⇔ y − = y = 0.25 A 1 0 A 1
Vậy đường thẳng(d) luôn đi qua điểm A(1; )
1 với mọi giá trị của m . 0.25 3
Cho đường tròn ( ;
O R) và dây cung BC cố định (BC < 2R). Điểm A di (5.0đ)
động trên đường tròn ( ;
O R) sao cho tam giác ABC nhọn. Kẻ đường
cao AD và trực tâm H của tam giác ABC .
a Đường thẳng chứa phân giác ngoài của góc BHC cắt AB, AC lần lượt
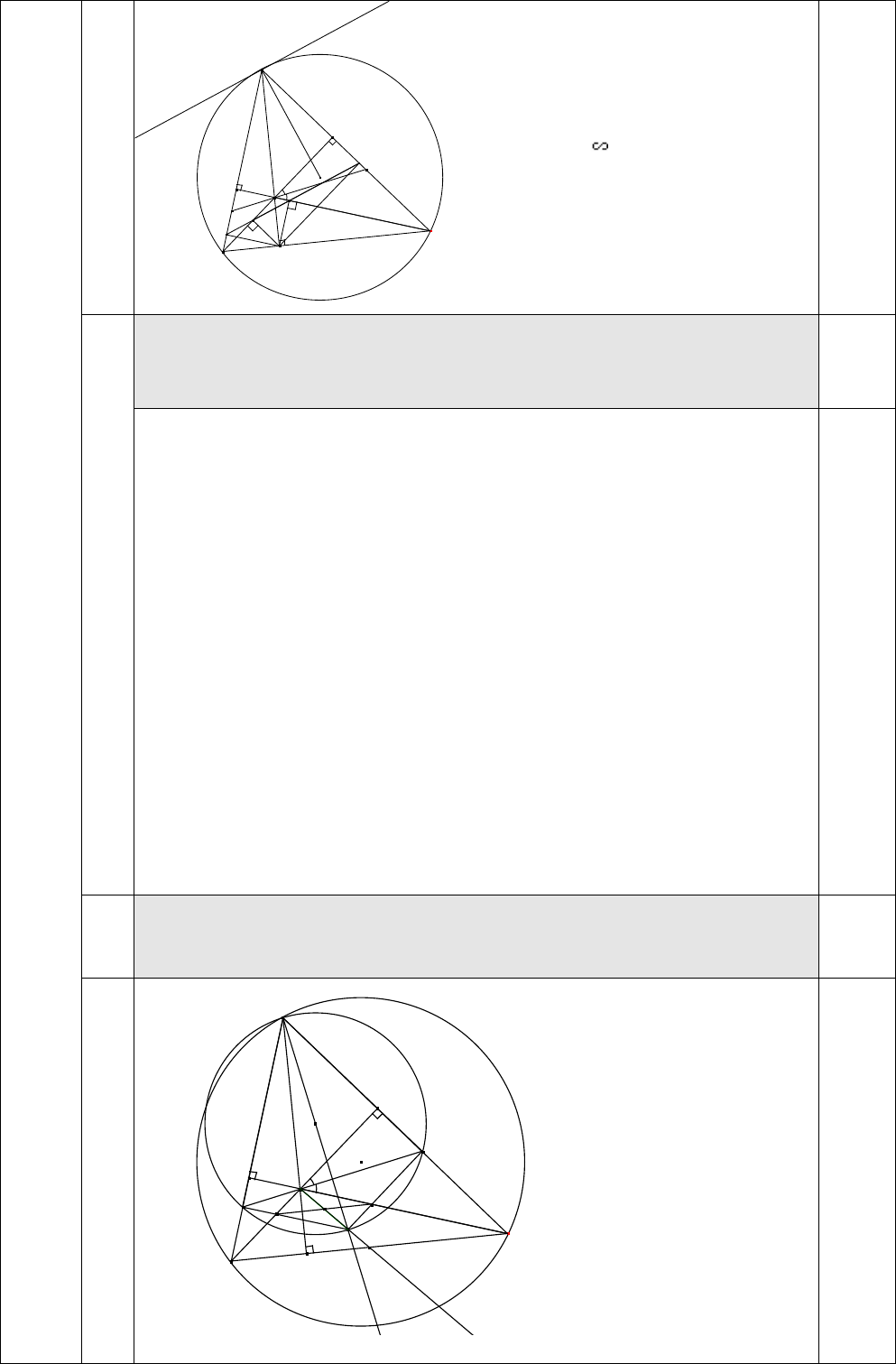
tại các điểm M , N . Chứng minh tam giác AMN cân. y Gọi '
B là hình chiếu của điểm B trên AC, '
C là hình chiếu của điểm A C trên AB. Ta có ' ' = =
C HM B HN ( NHC) 0.5 x B' ' Q ⇒ C ∆ HM ' B
∆ HN (g.g) 0.25 O N C' H ⇒ =
AMN ANM (t / c) M F E ⇒ A ∆ MN P cân tại A C 0.25 B D
b Các điểm E, F lần lượt là hình chiếu của D trên các đường thẳng
BH,CH . Các điểm P,Q lần lượt là hình chiếu của D trên các cạnh
AB, AC . Chứng minh 4 điểm P, E, F,Q thẳng hàng và OA ⊥ PQ . + Ta có =
PEB PDB (vì cùng chắn cung PB của đường tròn (BPED)) =
PDB HCD (vì đồng vị PD//CC’) =
HCD FDH (vì cùng phụ FHD ) =
FDH FEH (vì cùng chắn cung FH của đường tròn (DEHF)) ⇒ = PEB FEH 0.5
Mà 3 điểm B.E,H thẳng hàng nên 3 điểm P,E,F thẳng hàng. 0.25
Tương tự chứng minh được 3 điểm E,F,Q thẳng hàng.
Do đó 4 điểm P,E,F,Q thẳng hàng. 0.25
+ Kẻ xy là tiếp tuyến tại A của (O), Ta có =
xAB ACB (cùng chắn cung AB của (O)) Mà AP.AB = AQ.AC (=AD2) 0.25
⇒ tứ giác BPQC nội tiếp ⇒ = APQ ACB 0.25 ⇒ = xAB APQ ⇒ xy//PQ
Mà xy⊥ AO (t/c tiếp tuyến)
Do đó OA ⊥ PQ 0.5
c Đường tròn ngoại tiếp tam giác AMN cắt đường phân giác trong của
góc BAC tại K . Chứng minh đường thẳng HK luôn đi qua một điểm cố định.
Gọi U là giao điểm của BB’ A
và KM, V là giao điểm của CC’ và KN. + Ta có A ∆ MN cân tại A B' nên đường phân giác AK của góc MAN cũng là O N C'
đường trung trực của MN H
⇒ AK là đường kính của V M U (AMN). 0.5 K C ⇒ 0 AMK = 90 ' ⇒ MK / /CC B D hay UK / /HV Tương tự KV//UH nên tứ giác HVKU là hình bình hành
Đề HSG Toán 9 cấp tỉnh - Bình Phước năm 2022-2023 có đáp án
1.6 K
777 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Đề HSG Toán 9 cấp tỉnh - Bình Phước năm 2022-2023 có đáp án.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1553 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 9
Xem thêmTài liệu bộ mới nhất
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BÌNH PHƯỚC
(Đề gồm có 01 trang)
KÌ THI CHỌN HỌC SINH GIỎI
CẤP TỈNH LỚP 9 NĂM HỌC 2022 - 2023
MÔN: TOÁN
Thời gian làm bài:150 phút (Không kể thời gian phát đề)
Ngày thi: 18/03/2023
Câu 1: (5.0 điểm).
1. Cho biểu thức
3 29 39
:1
9
23 6
xx x x
P
x
x xx x
−+ − −
= +− −
−
− + +−
a) Tìm điều kiện xác định và rút gọn biểu thức
P
.
b) Tính giá trị của biểu thức
P
khi
3 3 13 48x =−− −
.
2. Cho
,,
xyz
là ba số thực khác
0
, thoả mãn
111
0
xyz
++=
.
Chứng minh rằng:
222
3
yz zx xy
xyz
++=
.
Câu 2: (5.0 điểm).
1. Giải phương trình:
3 1 31 0xx x+− + +− =
.
2. Giải hệ phương trình:
22
2
2
1
xy
xy
xy
xy x y
++ =
+
+= −
.
3.
Cho đường thẳng
( ) : ( 1) 2 1 0
d mx m y m+−−+=
(với
m
là tham số).
Tìm điểm cố định
mà đường thẳng
()
d
luôn đi qua với mọi giá trị của
m
.
Câu 3: (5.0 điểm). Cho đường tròn
( )
;OR
và dây cung
BC
cố định
(
)
2
BC R
<
. Điểm
A
di động trên đường tròn
( )
;OR
sao cho tam giác
ABC
nhọn. Kẻ đường cao
AD
và trực
tâm
H
của tam giác
ABC
.
a) Đường thẳng chứa phân giác ngoài của góc
BHC
cắt
,
AB AC
lần lượt tại các điểm
,
MN
. Chứng minh tam giác
AMN
cân.
b) Các điểm
,
EF
lần lượt là hình chiếu của
D
trên các đường thẳng
,BH CH
. Các
điểm
,PQ
lần lượt là hình chiếu của
D
trên các cạnh
,AB AC
. Chứng minh
4
điểm
,,,PEFQ
thẳng hàng và
OA PQ
⊥
.
c) Đường tròn ngoại tiếp tam giác
AMN
cắt đường phân giác trong của góc
BAC
tại
K
. Chứng minh đường thẳng
HK
luôn đi qua một điểm cố định.
Câu 4: (2.0 điểm). Cho tam giác
ABC
cân tại
A
, điểm
O
là trung điểm của
BC
. Đường
tròn
( )
O
tiếp xúc với các cạnh
AB
,
AC
lần lượt tại
,EF
. Điểm
H
chạy trên cung nhỏ
EF
của
( )
O
, tiếp tuyến của đường tròn
(
)
O
tại
H
cắt
,
AB AC
lần lượt tại
,MN
. Xác
định vị trí của điểm
H
để diện tích tam giác
AMN
đạt giá trị lớn nhất.
Câu 5: (3.0 điểm).
1. Cho
,,abc
là ba số thực dương, thoả mãn
1ab bc ca++=
.
Chứng minh rằng:
( )
42 42 42
5
2
9
a b b c c a abc a b c+ + + ≥ ++
.
2. Giải phương trình sau với nghiệm nguyên:
22
2 3 3 5 30x y xy x y+ + + + −=
.
…………… Hết ……………
• Thí sinh không được sử dụng tài liệu.
• Giám thị không giải thích gì thêm.
ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM KÌ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
NĂM HỌC 2022 – 2023
Môn: Toán - Lớp 9
(Hướng dẫn và biểu điểm gồm 05 trang)
Câu
Ý
Nội dung
Điểm
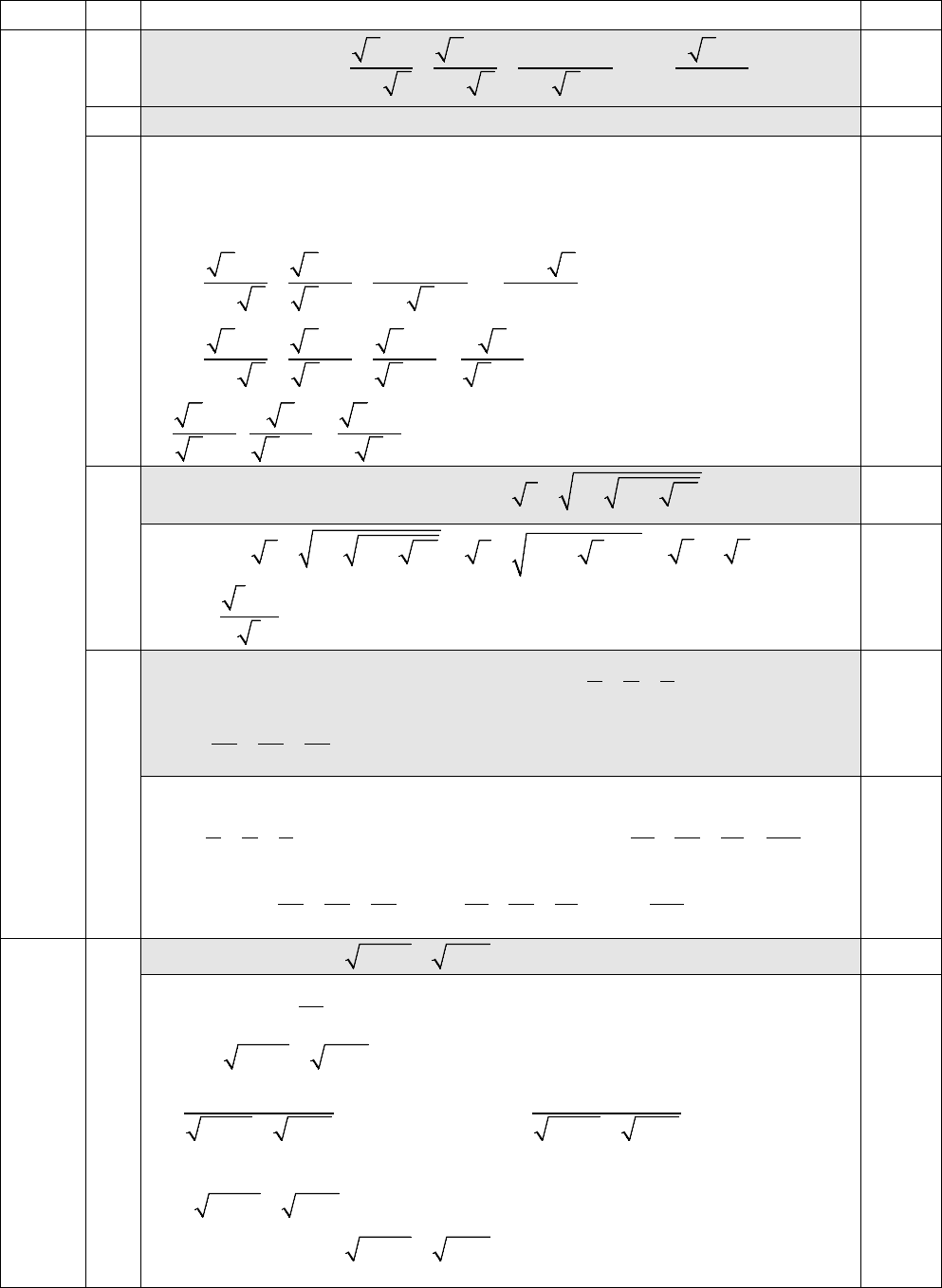
1
(5.0đ)
1
Cho biểu thức
3 29 39
:1
9
23 6
xx x x
P
x
x xx x
−+ − −
= +− −
−
− + +−
1.a
Tìm điều kiện xác định và rút gọn biểu thức
P
.
P
xác định
0
4
9
x
x
x
≥
⇔≠
≠
32 9 3
:
9
2 36
x x x xx
P
x
x x xx
−+ − −
= ++
−
− + +−
323
:
2 32 3
xxx x
P
xx x x
−+−
= ++
− +− +
2
:
33
xx
xx
+
=
++
2x
x
+
=
0.5
0.5
0.5
0.5
1.b
Tính giá trị của biểu thức
P
khi
3 3 13 48
x =−− −
.
Ta có
( )
3 3 13 48 3 3 2 3 1x =−− − =−− −
( )
3 31 1= − −=
12
3
1
P
+
⇒= =
0.75
0.25
2
Cho
,,xyz
là ba số thực khác
0
thoả mãn
111
0
xyz
++=
. Chứng minh
rằng:
222
3
yz zx xy
xyz
++=
+ Chứng minh được bài toán: Nếu
0abc++=
thì
333
3a b c abc++=
+ Vì
111
0
xyz
++=
và
,, 0xyz≠
nên suy ra được
3 33
111 3
x y z xyz
++=
Do đó
2 22 3 33
111 3
.3
yz zx xy
VT xyz xyz VP
x y z x y z xyz
=++= ++ = ==
(đpcm)
1.0
1.0
2
(5.0đ)
1
Giải phương trình:
3 1 31 0xx x+− + +− =
Điều kiện:
1
3
x
−
≥
Ta có:
3 1 31 0xx x+− + +− =
( )
22 2
1 0 1 10
31 3 31 3
x
xx
xx xx
−
⇔ +− = ⇔ − − =
++ + ++ +
1( )
3 1 32
xN
xx
=
⇔
++ + =
Giải phương trình:
3 1 32xx++ + =
0.25
0.5
0.25

4 4 2 (3 1)( 3) 4
x xx
⇒ ++ + + =
(3 1)( 3) 2xx x⇔ + +=−
(Đk:
0
x ≤
)
2
10 3 0xx⇒ − −=
5 27()
5 27( )
xL
xN
= +
⇔
= −
Vậy phương trình có 2 nghiệm là
12
1; 5 2 7
xx= = −
.
0.75
0.25
2
Giải hệ phương trình:
22
2
2
1 (1)
(2)
xy
xy
xy
xy x y
++ =
+
+= −
Điều kiện:
0xy+>
.
Biến đổi phương trình (1):
( )
2
22
22
1 2 10
xy xy
x y x y xy
xy xy
+ + =⇔ + − + −=
++
Đặt
,
x y S xy P+= =
(với
2
4SP≥
), ta có phương trình:
2
2
2 10
P
SP
S
+ − −=
3
22 0S P SP S⇔ + − −=
2
( 1) 2 ( 1) 0SS PS⇔ −− −=
2
2
1
( 1)( 2 ) 0
20
S
S SSP
SSP
=
⇔ − +− =⇔
+− =
+Với
1xy+=
thay vào (2) ta được:
( )
2
2
0
11 3 0
3
y
y yy y
y
=
=− −⇔ − =⇔
=
( )
( )
( )
{ }
; 1; 0 ; 2; 3xy⇒∈ −
+ Với
( )
2
2
20 2 0S S P xy xy xy+− =⇔ + ++− =
22
0x y xy⇔ + ++=
(Loại, vì
0
xy+>
).
Vậy hệ phương trình đã cho có 2 nghiệm
( )
;xy
là
( ) ( )
1; 0 ; 2; 3−
0.25
0.25
0.5
0.5
0.25
0.25
3
Cho đường thẳng
( ) : ( 1) 2 1 0
d mx m y m+−−+=
(với
m
là tham số).
Tìm
điểm cố định mà đường thẳng
()d
luôn đi qua với mọi giá trị của m.
Gọi
( )
;
AA
Ax y
là điểm cố định mà đường thẳng
()d
luôn đi qua với mọi
giá trị của m, ta có phương trình:
( )
( 1) 2 1 0 2 1
A A AA A
mx m y m x y m y+ − − += ⇔ + − = −
có nghiệm
m∀
20 1
10 1
AA A
AA
xy x
yy
+ −= =
⇔⇔
−= =
Vậy đường thẳng
()d
luôn đi qua điểm
( )
1;1A
với mọi giá trị của
m
.
0.5
0.25
0.25
3
(5.0đ)
Cho đường tròn
( )
;OR
và dây cung
BC
cố định
( )
2BC R<
. Điểm
A
di
động trên đường tròn
( )
;OR
sao cho tam giác
ABC
nhọn. Kẻ đường
cao
AD
và trực tâm
H
của tam giác
ABC
.
a
Đường thẳng chứa phân giác ngoài của góc
BHC
cắt
,AB AC
lần lượt
tại các điểm
,MN
. Chứng minh tam giác
AMN
cân.
Gọi
'
B
là hình chiếu của điểm B
trên AC,
'
C
là hình chiếu của điểm
C trên AB.
Ta có
( )
''
C HM B HN NHC= =
'
C HM⇒∆
( )
'
.B HN g g∆
( )
/AMN ANM t c⇒=
AMN⇒∆
cân tại A
0.5
0.25
0.25
b
Các điểm
,EF
lần lượt là hình chiếu của
D
trên các đường thẳng
,BH CH
. Các điểm
,PQ
lần lượt là hình chiếu của
D
trên các cạnh
,
AB AC
. Chứng minh
4
điểm
,,,
PEFQ
thẳng hàng và
OA PQ
⊥
.
+ Ta có
PEB PDB=
(vì cùng chắn cung PB của đường tròn (BPED))
PDB HCD=
(vì đồng vị PD//CC
’
)
HCD FDH=
(vì cùng phụ
FHD
)
FDH FEH=
(vì cùng chắn cung FH của đường tròn (DEHF))
PEB FEH⇒=
Mà 3 điểm B.E,H thẳng hàng nên 3 điểm P,E,F thẳng hàng.
Tương tự chứng minh được 3 điểm E,F,Q thẳng hàng.
Do đó 4 điểm P,E,F,Q thẳng hàng.
+ Kẻ xy là tiếp tuyến tại A của (O),
Ta có
xAB ACB=
(cùng chắn cung AB của (O))
Mà AP.AB = AQ.AC (=AD
2
)
⇒
tứ giác BPQC nội tiếp
⇒
APQ ACB=
⇒
xAB APQ=
⇒
xy//PQ
Mà xy
⊥
AO (t/c tiếp tuyến)
Do đó
OA PQ⊥
0.5
0.25
0.25
0.25
0.25
0.5
c
Đường tròn ngoại tiếp tam giác
AMN
cắt đường phân giác trong của
góc
BAC
tại
K
. Chứng minh đường thẳng
HK
luôn đi qua một điểm
cố định.
Gọi U là giao điểm của BB
’
và KM, V là giao điểm của
CC
’
và KN.
+ Ta có
AMN∆
cân tạ
i A
nên đườ
ng phân giác AK
của góc MAN cũng là
đường trung trực củ
a MN
⇒
AK là đường kính của
(AMN).
0
90AMK⇒=
'
//MK CC⇒
hay
//UK HV
Tương tự KV//UH nên tứ
giác HVKU là hình bình
hành
0.5
O
B
C
A
D
H
B'
M
N
C'
E
F
Q
P
x
y
O
B
C
A
D
H
B'
M
N
C'
K
U
V
⇒
HK đi qua trung điểm của UV (1)
+ Ta có
'
'
//
UB MB
MU C H
UH MC
⇒=
(ta lét), tương tự
'
VC NC
VH NB
=
Mà
''
MB HB
MC HC
=
(t/c đường phân giác của góc
'
BHC
),
tương tự
''
NC HC
NB HB
=
Mà
''
HB HC
HC HB
=
(vì
'
C HB∆
'
B HC∆
)
⇒
//
UB VC
UV BC
UH VH
= ⇒
(Ta lét đảo) (2)
Từ (1) và (2)
⇒
HK đi qua trung điểm của BC
Mà BC cố định nên HK luôn đi qua một điểm cố định.
0.5
0.25
0.25
0.25
0.25
4
(2.0đ)
Cho tam giác
ABC
cân tại
A
, điểm
O
là trung điểm của
BC
. Đường
tròn
O
tiếp xúc với các cạnh
AB
,
AC
lần lượt tại
,EF
. Điểm
H
chạy
trên cung nhỏ
EF
của
O
, tiếp tuyến của đường tròn
O
tại
H
cắt
,
AB AC
lần lượt tại
,MN
. Xác định vị trí của điểm
H
để diện tích tam
giác
AMN
đạt giá trị lớn nhất.
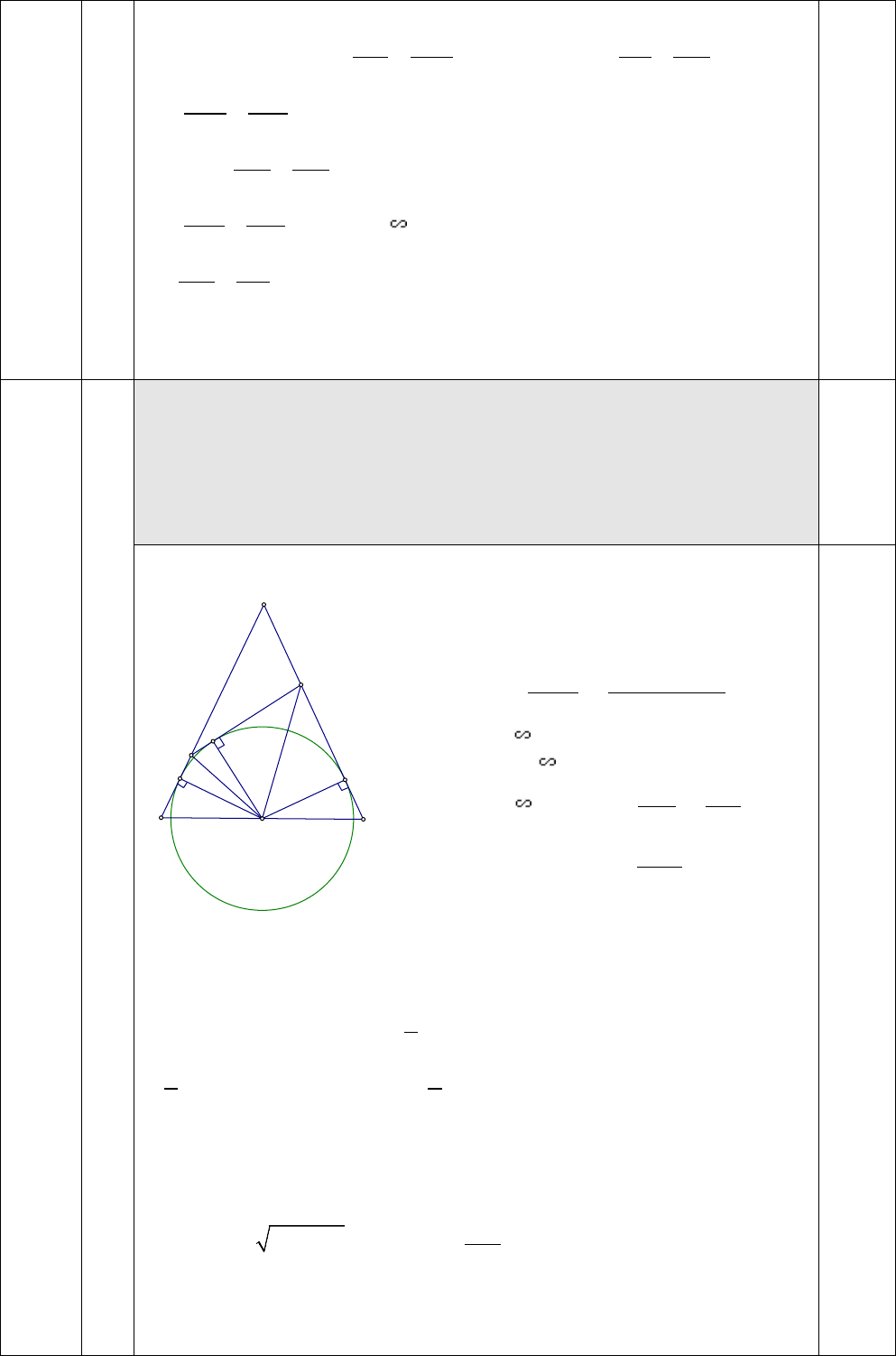
+ Ta có
,OM ON
lần lượt là phân giác
,
EOM FOH
(t/c 2 tiếp tuyến cắt nhau của
O
)
0
180
22
EOF BAC
MON ABC
MBO
MON
(g.g)
Cmtt
OCN
MON
MBO
OCN
MB BO
OC CN
2
..
4
BC
BM CN OBOC const
(1)
+ Lại có
AMN ABC BMNC
S SS= −
AMN
S
đạt giá trị lớn nhất khi và chỉ khi
BMNC
S
đạt giá trị nhỏ nhất.
Gọi
R
là bán kính của đường tròn
O
, ta có:
( )
1
2
BMNC BOM MON NOC
S S S S R BM MN NC= + + = ++
( )
( )
11
2 22
22
R BM NC EM FN R BM CN BE
= ++ + = + −
( )
R BM CN BE= +−
(Vì
, ,;BE CF ME MH NF NH MH NH MN= = = +=
)
Áp dụng bất đẳng thức Cauchy, từ (1) và (2) suy ra:
. onst
2
BMNC
BC
S R BM CN BE R BE c
.
(Vì
ABC
cố định nên BC và BE không đổi)
0.5
0.5
0.5
O
H
F
E
N
M
C
B
A