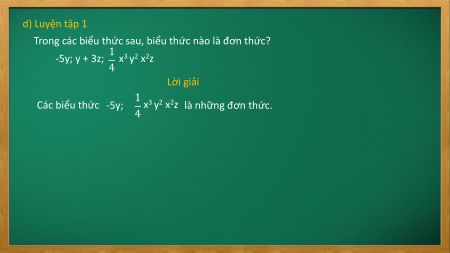CHƯƠNG I: ĐA THỨC NHIỀU BIẾN
BÀI 1: ĐƠN THỨC NHIỀU BIẾN. ĐA THỨC NHIỀU BIẾN.
CHƯƠNG I: ĐA THỨC NHIỀU BIẾN
BÀI 1: ĐƠN THỨC NHIỀU BIẾN. ĐA THỨC NHIỀU BIẾN.
I. ĐƠN THỨC NHIỀU BIẾN 1. Khái niệm HĐ1
a) Viết biểu thức biểu thị:
- Diện tích hình vuông có độ dài cạnh là x (cm);
- Diện tích hình chữ nhật có độ dài hai cạnh lần lượt là 2x (cm); 3y (cm);
- Thể tích của hình hộp chữ nhật có ba kích thước lần lượt là x(cm); 2y (cm); 3z (cm)
b) Cho biết mỗi biểu thức trên gồm những số, biến và phép tính nào? Lời giải a) x.x ; 2x .3y; x. 2y .3z
b) Biểu thức x .x gồm biến x và phép tính nhân.
Biểu thức 2x.3y gồm các số 2; 3 ; các biến x, y và phép tính nhân.
Biểu thức x.2y.3z gồm các số 2; 3 ; các biến x, y,z và phép tính nhân.
CHƯƠNG I: ĐA THỨC NHIỀU BIẾN
BÀI 1: ĐƠN THỨC NHIỀU BIẾN. ĐA THỨC NHIỀU BIẾN.
I. ĐƠN THỨC NHIỀU BIẾN b) Khái niệm
Đơn thức nhiều biến (đơn thức) là biểu thức đại số chỉ gồm một số hoặc một biến hoặc
một tích giữa các số và các biến. c) Ví dụ:
Trong các biểu thức sau, biểu thức nào là đơn thức? 1 -3; x; a + 4; y2; 0,5ab; x 2 yz ; 3 x – 2y 4 Lời giải 1 -3; x; y2; 0,5ab;
x2yz3 là những đơn thức 4 d) Luyện tập 1
Trong các biểu thức sau, biểu thức nào là đơn thức? 1 -5y; y + 3z; x3 y2 x2z 4 Lời giải 1 Các biểu thức -5y;
x3 y2 x2z là những đơn thức. 4
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26