CHUYÊN ĐỀ 23:
MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN
I - DẠNG TOÁN DÙNG PHƯƠNG PHÁP GIẢ THIẾT TẠM A – LÝ THUYẾT 1. Khái niệm:
Phương pháp giả thiết tạm là phương pháp áp dụng để giải các bài toán mà phần cần
tìm gồm ít nhất hai số chưa biết, còn phần đã cho gồm một điều kiện ràng buộc các
số chưa biết đó với nhau. Ý tưởng của phương pháp này là nhờ một giả thiết tự đặt ra
một cách thích hợp (giả thiết tạm) ta khử bớt các yếu tố tham gia vào các điều kiện đã
cho, trên cơ sở đó tìm ra một số chưa biết, rồi lần lượt tìm các số còn lại
2. Ví dụ: Bài toán:
“Thuyền to chở được sáu người,
Thuyền nhỏ chở được bốn người là đông,
Một đoàn trai gái sang sông,
Mười thuyền to nhỏ giữa dòng đang trôi,
Toàn đoàn có cả trăm người,
Trên bờ còn bốn tám người đợi sang”.
Hỏi trên sông có bao nhiêu thuyền to, nhỏ mỗi loại? Bài giải Cách 1:
Số người ở trên thuyền là: 100 – 48 = 52 (người)
Giả sử tất cả các thuyền là thuyền to.
Khi ấy số người trên thuyền là: 10 6 = 60 (người)
Số người dư ra là: 60 – 52 = 8 (người)
Số người ở trên thuyền nhỏ ít hơn số người ở trên thuyền to là: 6 – 4 = 2 (người)
Số thuyền nhỏ là: 8 : 2 = 4 (thuyền)
Số thuyền to là:10 – 4 = 6 (thuyền)
Đáp số: Thuyền to : 6 thuyền; Thuyền nhỏ: 4 thuyền Cách 2:
Số người ở trên thuyền là: 100 – 48 = 52 (người)
Giả sử tất cả các thuyền là thuyền nhỏ.
Khi ấy số người trên thuyền là: 10 4 = 40 (người)
Số người dư ra là: 52 – 40 = 12 (người)
Số người ở trên thuyền to hơn số người ở trên thuyền nhỏ là: 6 – 4 = 2 (người)
Số thuyền to là: 12 : 2 = 6 (thuyền)
Số thuyền nhỏ là:10 – 6 = 4 (thuyền)
Đáp số: Thuyền to : 6 thuyền; Thuyền nhỏ: 4 thuyền Cách 3:
Số người ở trên thuyền là: 100 – 48 = 52 (người)
Giả sử mỗi thuyền to chỉ chở lại một nửa số người quy định.
Khi đó số người còn lại ở 10 thuyền là: 52 : 2 = 26 (người)
Khi ấy thuyền to chỉ chở được 3 người, thuyền nhỏ chỉ chở được 2 người.
Giả sử mỗi thuyền lại bớt đi 2 người khi ấy thuyền nhỏ không còn người nào, thuyền
to chỉ chở được 1 người, số người còn lại là:
36 – (10 2) = 6 (người)
Vì mỗi thuyền to còn một người nên số thuyền to là 6 (thuyền)
Số thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: Thuyền to : 6 thuyền, Thuyền nhỏ: 4 thuyền Cách 4:
Số người trên thuyền là: 100 – 48 = 52 (người)
Giả sử mỗi thuyền cùng bớt 2 người thì 10 thuyền còn số người là:
52 – (10 2) = 32 (người). Khi ấy thuyền nhỏ còn 2 người, thuyền to còn 4 người.
Giả sử mỗi thuyền lại bớt tiếp 2 người nữa. Khi ấy thuyền nhỏ không có người,
thuyền to còn hai người. Số người của 10 thuyền là 32 – 20 = 12 (người).
12 người đó là của thuyền to, mỗi thuyền to có 2 người nên số thuyền to là: 12 : 2 = 6 (thuyền)
Sổ thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: Thuyền to : 6 thuyền, Thuyền nhỏ: 4 thuyền Cách 5:
Số người trên thuyền là: 100 – 48 = 52 (người)
Giá sử cứ 2 thuyền to thay bằng 3 thuyền nhỏ. Khi đó mỗi lần thay số thuyền tăng là: 3 – 2 = 1 (thuyền)
Số thuyền lúc ấy là: 52 : 4 = 13 (thuyền)
Sổ thuyền tăng là: 13 – 10 = 3 (thuyền)
Khi đó số lần thay là 3 lần.
Vậy số thuyền to là: 2 3 = 6 (thuyền)
Số thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: 6 thuyền to, 4 thuyền nhỏ Cách 6:
Số người trên thuyền là: 100 – 48 = 52 (người)
Giả sử số thuyền to bằng số thuyền nhỏ. Khi đó số thuyền to là 5 thuyền, số thuyền nhỏ là 5 thuyền.
Số người trên thuyền là: 4 5 + 6 5 = 50 (người)
Số người thiếu là: 52 – 50 = 2 (người)
Để số thuyền to và số thuyền nhỏ không đổi, ta thực hiện thay cứ một thuyền nhỏ
bằng một thuyền to thì số thuyền to tăng lên là một thuyền và số thuyền nhỏ giảm đi một thuyền.
Mỗi lần thay số người tăng lên là: 6 – 4 = 2 (người)
Ta cần thực hiện số lần thay là: 2 : 2 = 1 (lần)
Vậy số thuyền to là: 5 + 1 = 6 (thuyền)
Số thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: 6 thuyền to; 4 thuyền nhỏ
II - Phương pháp suy luận logic.
- Xét trường hợp xấu nhất (tốt nhất) có thể xảy ra
Ví dụ: Trong hộp có 102 viên bi đỏ, 120 viên bi vàng và 150 viên bi xanh. Theo em
không nhìn vào hộp, phải lấy ra ít nhất bao nhiêu viên bi để chắc chắn số bi lấy ra có
đủ 3 màu và mỗi màu phải có nhiều hơn 2 viên? BÀI GIẢI
Số viên bi phải lấy ra ít nhất để số bi lấy là có đủ 3 màu và mỗi màu nhiều hơn 2 viên
là: 150 + 120 + 3 = 273 (viên) Đáp số: 273 viên
III - Phương pháp giải toán bằng biểu đồ ven.
Trong khi giải bài toán, người ta thường dùng những đường cong kín để mô tả
mối quan hệ giữa các đại lượng trong bài toán. Nhờ sự mô tả này mà ta giải được bài
toán 1 cách thuận lợi. Những đường cong như thế gọi là biểu đồ VEN.
Ví dụ 1: Lớp học có 53 học sinh, qua điều tra thấy 40 em thích học môn văn,
30 em thích học môn toán. Hỏi có nhiều nhất bao nhiêu học sinh thích học 2 môn ?
có ít nhất bao nhiêu học sinh thích học 2 môn ? nếu có 3 học sinh không thích học 2
môn thì lúc này có bao nhiêu học sinh thích học 2 môn. Hướng dẫn
Số học sinh chỉ thích môn Văn là: 53 – 30 = 23 (em)
Số học sinh chỉ thích môn Toán là: 53 – 40 = 13 (em)
Số học sinh thích cả 2 môn Toán và Văn là: 53 – (23 + 13) = 17 (em) Ví dụ 2:
Lớp 4A có 30 em tham gia dạ hội tiếng Anh và tiếng Trung, trong đó có 25 em
nói được tiếng Anh và 18 em nói được tiếng Trung. Hỏi có bao nhiêu bạn nói được cả 2 thứ tiếng? Hướng dẫn
Các em lớp 4A tham gia dạ hội được mô tả bằng sơ đồ ven.
Chuyên đề Một số phương pháp giải toán lớp 4 (có lời giải)
1.2 K
592 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Trọn bộ 24 Chuyên đề Toán lớp 4 đầy đủ lý thuyết và các dạng bài tập đa dạng có lời giải từ cơ bản đến nâng cao mới nhất năm 2023-2024 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 4.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1183 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 4
Xem thêmTài liệu bộ mới nhất
CHUYÊN ĐỀ 23:
MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN
I - DẠNG TOÁN DÙNG PHƯƠNG PHÁP GIẢ THIẾT TẠM
A – LÝ THUYẾT
1. Khái niệm:
Phương pháp giả thiết tạm là phương pháp áp dụng để giải các bài toán mà phần cần
tìm gồm ít nhất hai số chưa biết, còn phần đã cho gồm một điều kiện ràng buộc các
số chưa biết đó với nhau. Ý tưởng của phương pháp này là nhờ một giả thiết tự đặt ra
một cách thích hợp (giả thiết tạm) ta khử bớt các yếu tố tham gia vào các điều kiện đã
cho, trên cơ sở đó tìm ra một số chưa biết, rồi lần lượt tìm các số còn lại
2. Ví dụ: Bài toán:
“Thuyền to chở được sáu người,
Thuyền nhỏ chở được bốn người là đông,
Một đoàn trai gái sang sông,
Mười thuyền to nhỏ giữa dòng đang trôi,
Toàn đoàn có cả trăm người,
Trên bờ còn bốn tám người đợi sang”.
Hỏi trên sông có bao nhiêu thuyền to, nhỏ mỗi loại?
Bài giải
Cách 1:
Số người ở trên thuyền là: 100 – 48 = 52 (người)
Giả sử tất cả các thuyền là thuyền to.
Khi ấy số người trên thuyền là: 10 6 = 60 (người)
Số người dư ra là: 60 – 52 = 8 (người)
Số người ở trên thuyền nhỏ ít hơn số người ở trên thuyền to là: 6 – 4 = 2 (người)
Số thuyền nhỏ là: 8 : 2 = 4 (thuyền)
Số thuyền to là:10 – 4 = 6 (thuyền)
Đáp số: Thuyền to : 6 thuyền; Thuyền nhỏ: 4 thuyền
Cách 2:
Số người ở trên thuyền là: 100 – 48 = 52 (người)
Giả sử tất cả các thuyền là thuyền nhỏ.
Khi ấy số người trên thuyền là: 10 4 = 40 (người)
Số người dư ra là: 52 – 40 = 12 (người)
Số người ở trên thuyền to hơn số người ở trên thuyền nhỏ là: 6 – 4 = 2 (người)
Số thuyền to là: 12 : 2 = 6 (thuyền)
Số thuyền nhỏ là:10 – 6 = 4 (thuyền)
Đáp số: Thuyền to : 6 thuyền; Thuyền nhỏ: 4 thuyền
Cách 3:
Số người ở trên thuyền là: 100 – 48 = 52 (người)
Giả sử mỗi thuyền to chỉ chở lại một nửa số người quy định.
Khi đó số người còn lại ở 10 thuyền là: 52 : 2 = 26 (người)
Khi ấy thuyền to chỉ chở được 3 người, thuyền nhỏ chỉ chở được 2 người.
Giả sử mỗi thuyền lại bớt đi 2 người khi ấy thuyền nhỏ không còn người nào, thuyền
to chỉ chở được 1 người, số người còn lại là:
36 – (10 2) = 6 (người)
Vì mỗi thuyền to còn một người nên số thuyền to là 6 (thuyền)
Số thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: Thuyền to : 6 thuyền, Thuyền nhỏ: 4 thuyền
Cách 4:
Số người trên thuyền là: 100 – 48 = 52 (người)
Giả sử mỗi thuyền cùng bớt 2 người thì 10 thuyền còn số người là:
52 – (10 2) = 32 (người). Khi ấy thuyền nhỏ còn 2 người, thuyền to còn 4 người.
Giả sử mỗi thuyền lại bớt tiếp 2 người nữa. Khi ấy thuyền nhỏ không có người,
thuyền to còn hai người. Số người của 10 thuyền là
32 – 20 = 12 (người).
12 người đó là của thuyền to, mỗi thuyền to có 2 người nên số thuyền to là:
12 : 2 = 6 (thuyền)
Sổ thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: Thuyền to : 6 thuyền, Thuyền nhỏ: 4 thuyền
Cách 5:
Số người trên thuyền là: 100 – 48 = 52 (người)
Giá sử cứ 2 thuyền to thay bằng 3 thuyền nhỏ. Khi đó mỗi lần thay số thuyền tăng là:
3 – 2 = 1 (thuyền)
Số thuyền lúc ấy là: 52 : 4 = 13 (thuyền)
Sổ thuyền tăng là: 13 – 10 = 3 (thuyền)
Khi đó số lần thay là 3 lần.
Vậy số thuyền to là: 2 3 = 6 (thuyền)
Số thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: 6 thuyền to, 4 thuyền nhỏ
Cách 6:
Số người trên thuyền là: 100 – 48 = 52 (người)
Giả sử số thuyền to bằng số thuyền nhỏ. Khi đó số thuyền to là 5 thuyền, số thuyền
nhỏ là 5 thuyền.
Số người trên thuyền là: 4 5 + 6 5 = 50 (người)
Số người thiếu là: 52 – 50 = 2 (người)
Để số thuyền to và số thuyền nhỏ không đổi, ta thực hiện thay cứ một thuyền nhỏ
bằng một thuyền to thì số thuyền to tăng lên là một thuyền và số thuyền nhỏ giảm đi
một thuyền.
Mỗi lần thay số người tăng lên là: 6 – 4 = 2 (người)
Ta cần thực hiện số lần thay là: 2 : 2 = 1 (lần)
Vậy số thuyền to là: 5 + 1 = 6 (thuyền)
Số thuyền nhỏ là: 10 – 6 = 4 (thuyền)
Đáp số: 6 thuyền to; 4 thuyền nhỏ
II - Phương pháp suy luận logic.
- Xét trường hợp xấu nhất (tốt nhất) có thể xảy ra
Ví dụ: Trong hộp có 102 viên bi đỏ, 120 viên bi vàng và 150 viên bi xanh. Theo em
không nhìn vào hộp, phải lấy ra ít nhất bao nhiêu viên bi để chắc chắn số bi lấy ra có
đủ 3 màu và mỗi màu phải có nhiều hơn 2 viên?
BÀI GIẢI

Số viên bi phải lấy ra ít nhất để số bi lấy là có đủ 3 màu và mỗi màu nhiều hơn 2 viên
là: 150 + 120 + 3 = 273 (viên)
Đáp số: 273 viên
III - Phương pháp giải toán bằng biểu đồ ven.
Trong khi giải bài toán, người ta thường dùng những đường cong kín để mô tả
mối quan hệ giữa các đại lượng trong bài toán. Nhờ sự mô tả này mà ta giải được bài
toán 1 cách thuận lợi. Những đường cong như thế gọi là biểu đồ VEN.
Ví dụ 1: Lớp học có 53 học sinh, qua điều tra thấy 40 em thích học môn văn,
30 em thích học môn toán. Hỏi có nhiều nhất bao nhiêu học sinh thích học 2 môn ?
có ít nhất bao nhiêu học sinh thích học 2 môn ? nếu có 3 học sinh không thích học 2
môn thì lúc này có bao nhiêu học sinh thích học 2 môn.
Hướng dẫn
Số học sinh chỉ thích môn Văn là: 53 – 30 = 23 (em)
Số học sinh chỉ thích môn Toán là: 53 – 40 = 13 (em)
Số học sinh thích cả 2 môn Toán và Văn là: 53 – (23 + 13) = 17 (em)
Ví dụ 2:
Lớp 4A có 30 em tham gia dạ hội tiếng Anh và tiếng Trung, trong đó có 25 em
nói được tiếng Anh và 18 em nói được tiếng Trung. Hỏi có bao nhiêu bạn nói được cả
2 thứ tiếng?
Hướng dẫn
Các em lớp 4A tham gia dạ hội được mô tả bằng sơ đồ ven.
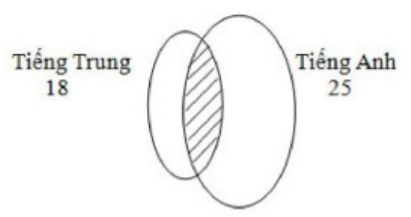
Số học sinh chỉ nói được tiếng Trung là: 30 – 25 = 5 (em)
Số học sinh chỉ nói được tiếng Anh là: 30 – 18 = 12 (em)
Số em nói được cả 2 thứ tiếng là: 30 – (5 + 12) = 13 (em)
Đáp số: 13 em.
B - BÀI TẬP
Bài 1. 2 người thợ làm chung một công việc thì phải làm trong 7 giờ mới xong.
Nhưng người thợ cả chỉ làm 4 giờ rồi nghỉ do đó người thứ hai phải làm 9 giờ nữa
mới xong. Hỏi nếu làm riêng thì mỗi người phải làm mấy giờ mới xong?
Bài 2. Có một số dầu hỏa, nếu đổ vào các can 6 lít thì vừa hết. Nếu đổ vào các can 10
lít thì thừa 2 lít và số can giảm đi 5can. Hỏi có bao nhiêu lít dầu?
Bài 3. Cô giáo đem chia một số kẹo cho các em. Cô nhẩm tính, nếu chia cho mỗi em
5 chiếc thì thừa 3 chiếc, nếu chia cho mỗi em 6 chiếc thì thiếu 5 chiếc. Hỏi cô giáo có
bao nhiêu cái kẹo?
Bài 4. Có 145 tờ tiền mệnh giá 5000đ, 2000đ và 1000đ. Số tiền của 145 tờ tiền giấy
trên là 312 000đ. Số tiền loại mệnh giá 2000đ gấp đôi loại 1000đ. Hỏi mỗi loại tiền
có mấy tờ.
Bài 5. Bác Toàn mua 5 cái bàn và 7 cái ghế với tổng tiền phải trả là 3 010 000 đồng .
Giá 1 cái bàn đất hơn 1 cái ghế 170 000 đồng. Nếu mua 1 cái bàn và 2 cái ghế thì hết
bao nhiêu tiền?
Bài 6. Một nhóm học sinh lớp 4 tham gia sinh hoạt ngoại khóa được chia thành các tổ
để sinh hoạt. Nếu mỗi tổ 6 nam và 6 nữ thì thừa 20 bạn nam. Nếu mỗi tổ 7 nam và 5
nữ thì thừa 20 nữ. Hỏi có bao nhiêu nam, bao nhiêu nữ?























