Giáo án Powerpoint Đường tiệm cận Toán 12 Giải tích

LỚP ĐẠI SỐ 12
Chương 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Bài 4. ĐƯỜNG TIỆM CẬN
I ĐƯỜNG TIỆM CẬN NGANG
II ĐƯỜNG TIỆM CẬN ĐỨNG
Tính các giới hạn sau 1. 2. Bài giải 1. 2. Vì và I ĐƯỜNG TIỆM CẬN NGANG Ví dụ 1
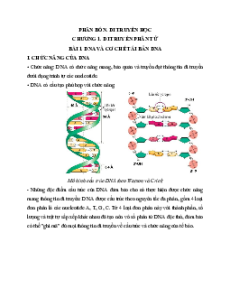
Quan sát đồ thị của hàm số ở hình vẽ dưới đây. Nêu nhận xét về
khoảng cách từ điểm đến đường thẳng khi và kiểm tra nhận xét trên
bằng cách tính giới hạn. Bài giải
Gọi là hình chiếu của lên đường thẳng ?
Khi càng lớn thì điểm trên đồ thị và điểm trên đường
đường thẳng càng gần nhau.
Nên khoảng cách từ đến càng dần đến bằng khi ? ?
Thật vậy, khoảng cách từ đến là: ? ? Ta có: = . ? ? ? Tương tự: = . Suy ra và . I ĐƯỜNG TIỆM CẬN Đị NGA nh NG nghĩa
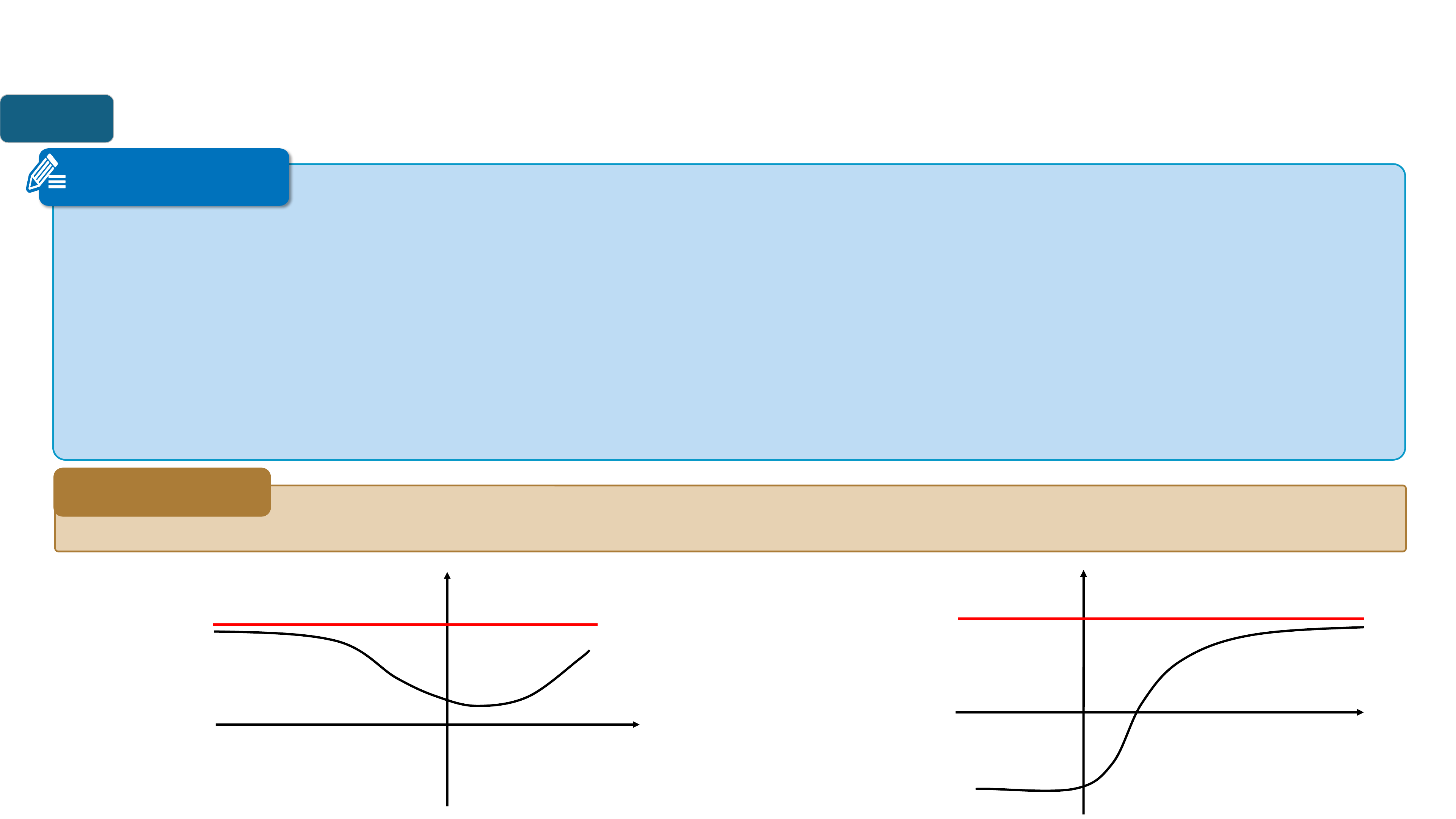
Cho hàm số xác định trên một khoảng vô hạn (là
khoảng dạng hoặc ). Đường thẳng được gọi là đường tiệm cận
ngang (hay tiệm cận ngang) của đồ thị hàm số nếu ít nhất một trong
các điều kiện sau được thỏa mãn
??? ? ( ? )=?
??? ? ( ?)=? ? ?
? →+ ∞ ? → −∞ Chú ý
Nếu thì ta viết chung là . Khi y Khi y y y0 0 O x O x