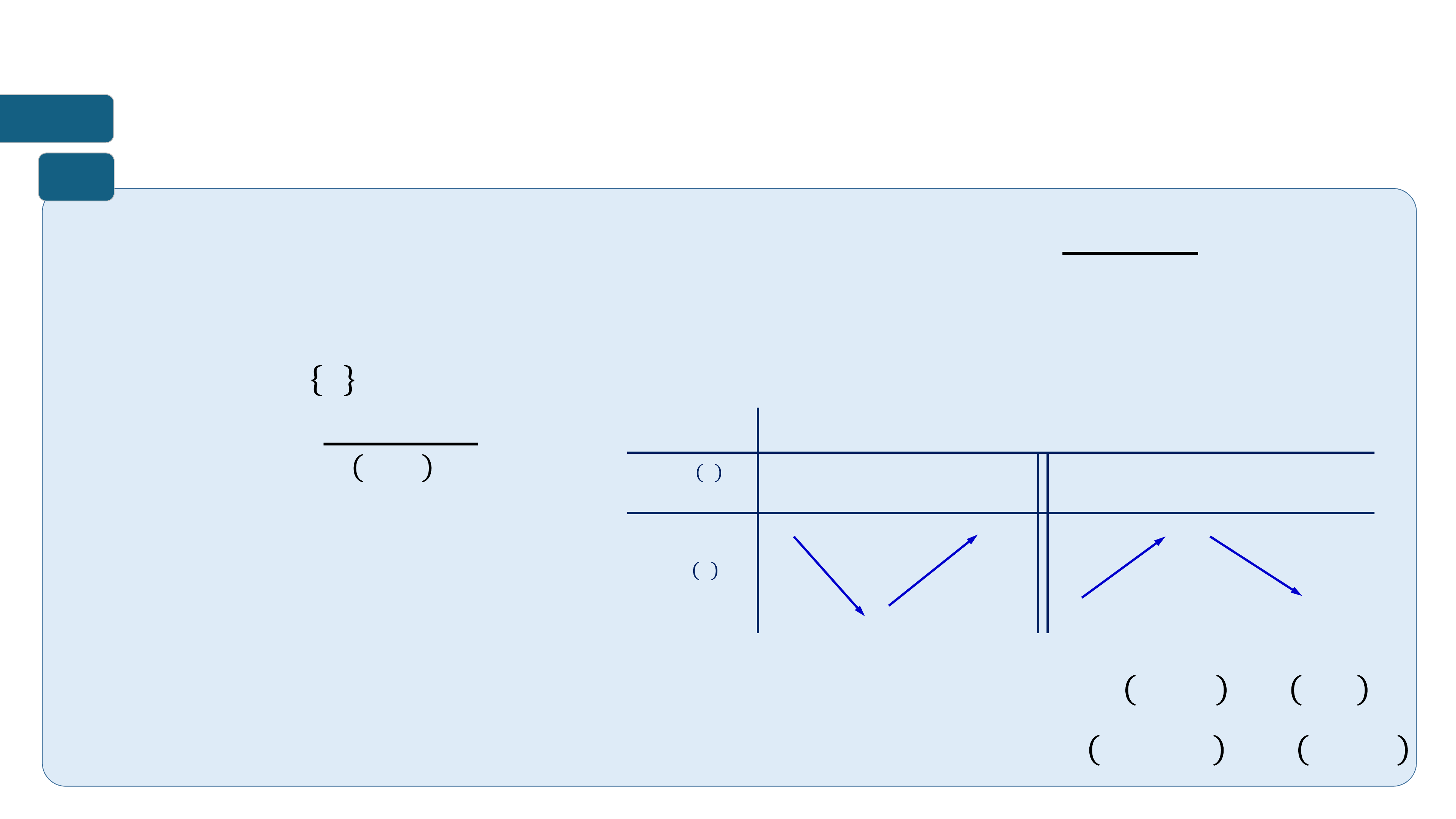LỚP GIẢI TÍCH12
Chương 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HS VÀ VẼ ĐỒ THỊ HS
Bài 1. SỰ ĐỒNG BIẾN VÀ NGHỊCH BIẾN CÙA HÀM SỐ I
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1 Nhắc lại định nghĩa
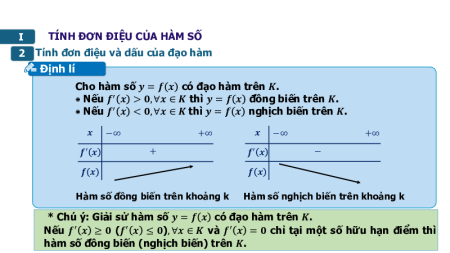
2 Tính đơn điệu và dấu của đạo hàm 3 Ví dụ II
QUY TẮC XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 1 Quy tắc 2 Áp dụng
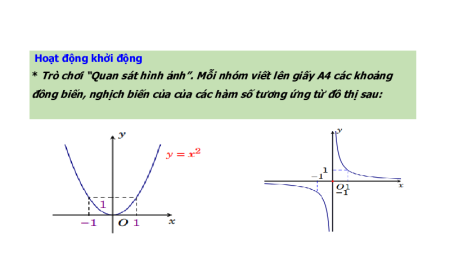
Hoạt động khởi động
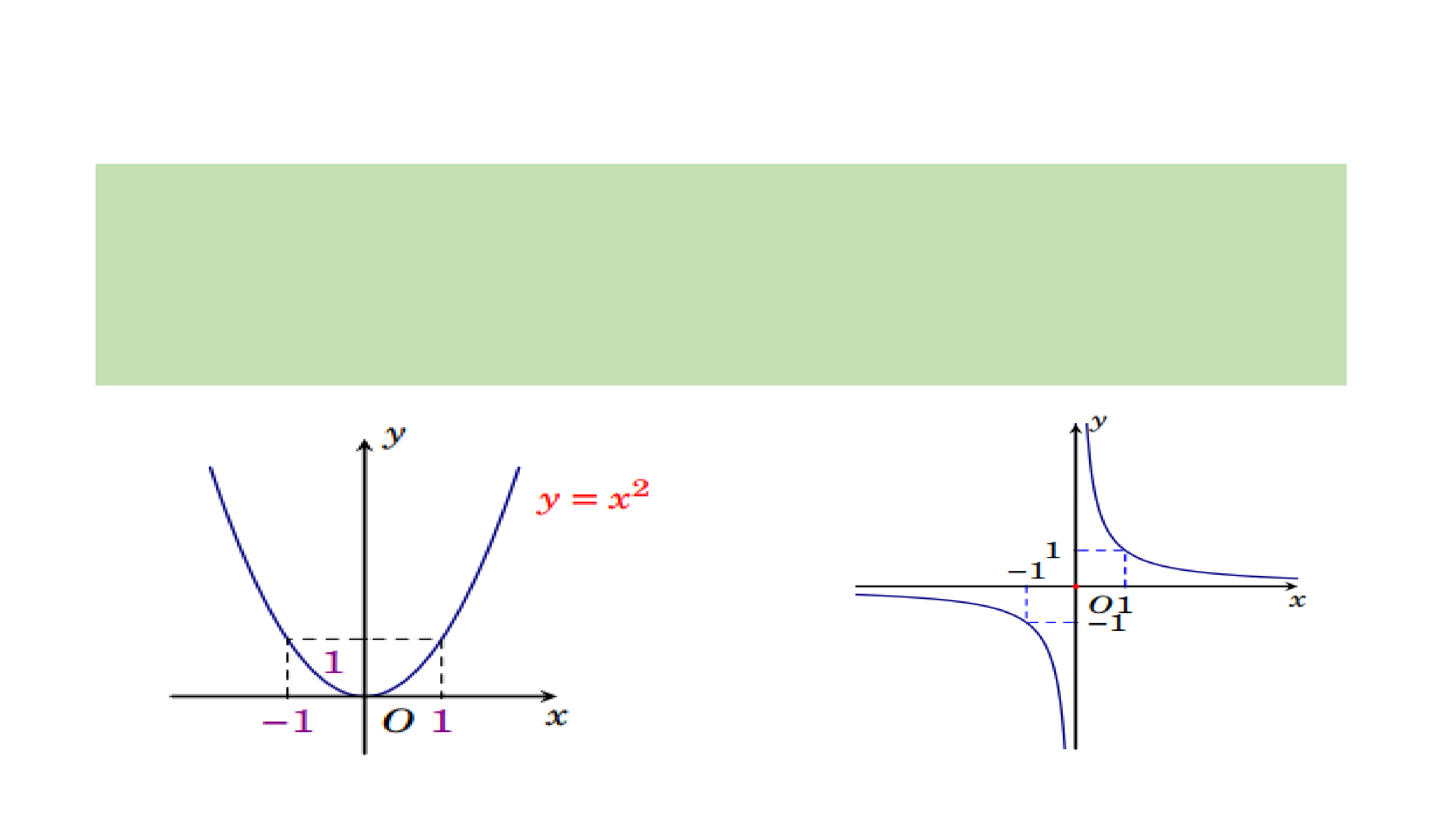
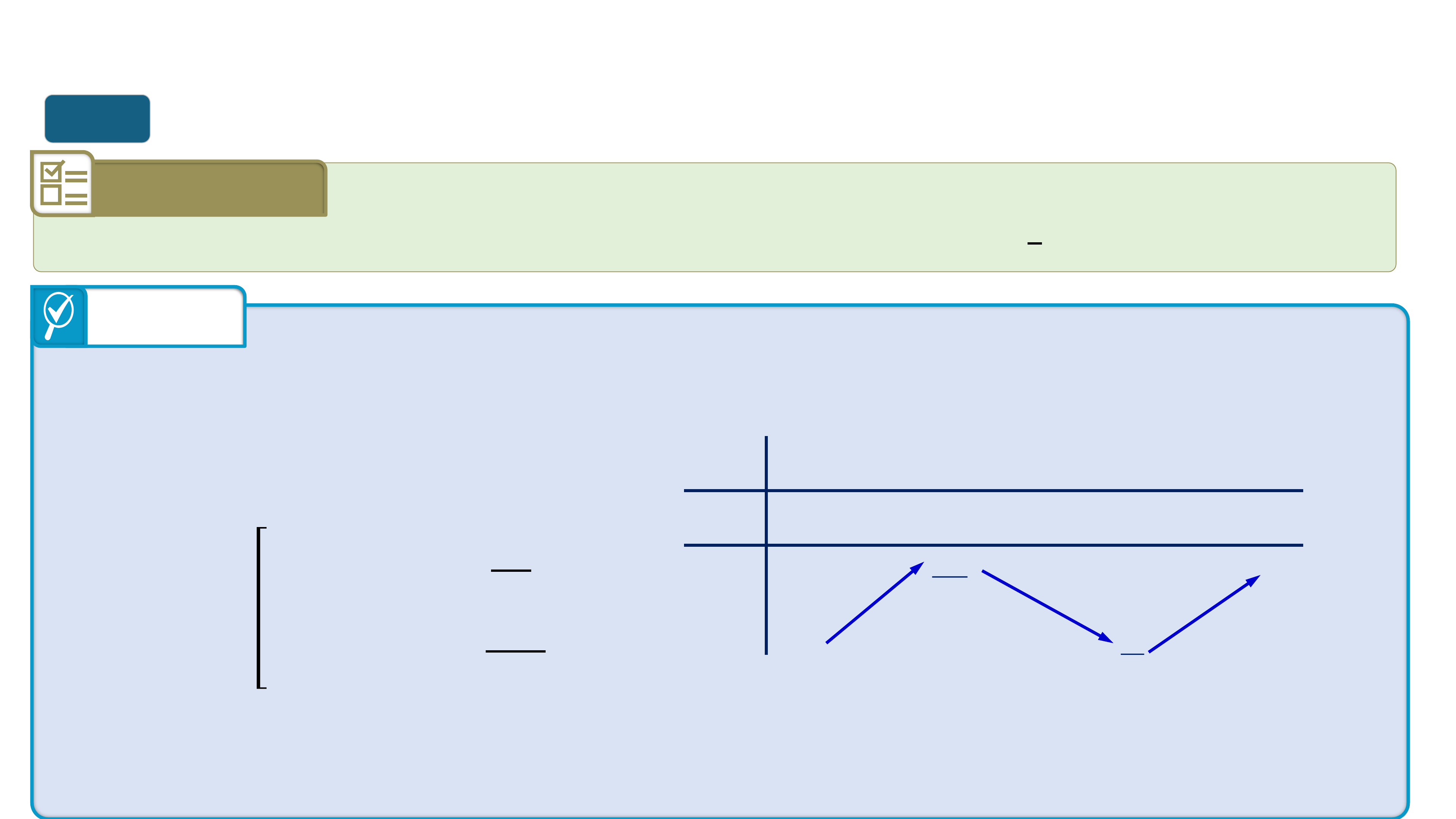
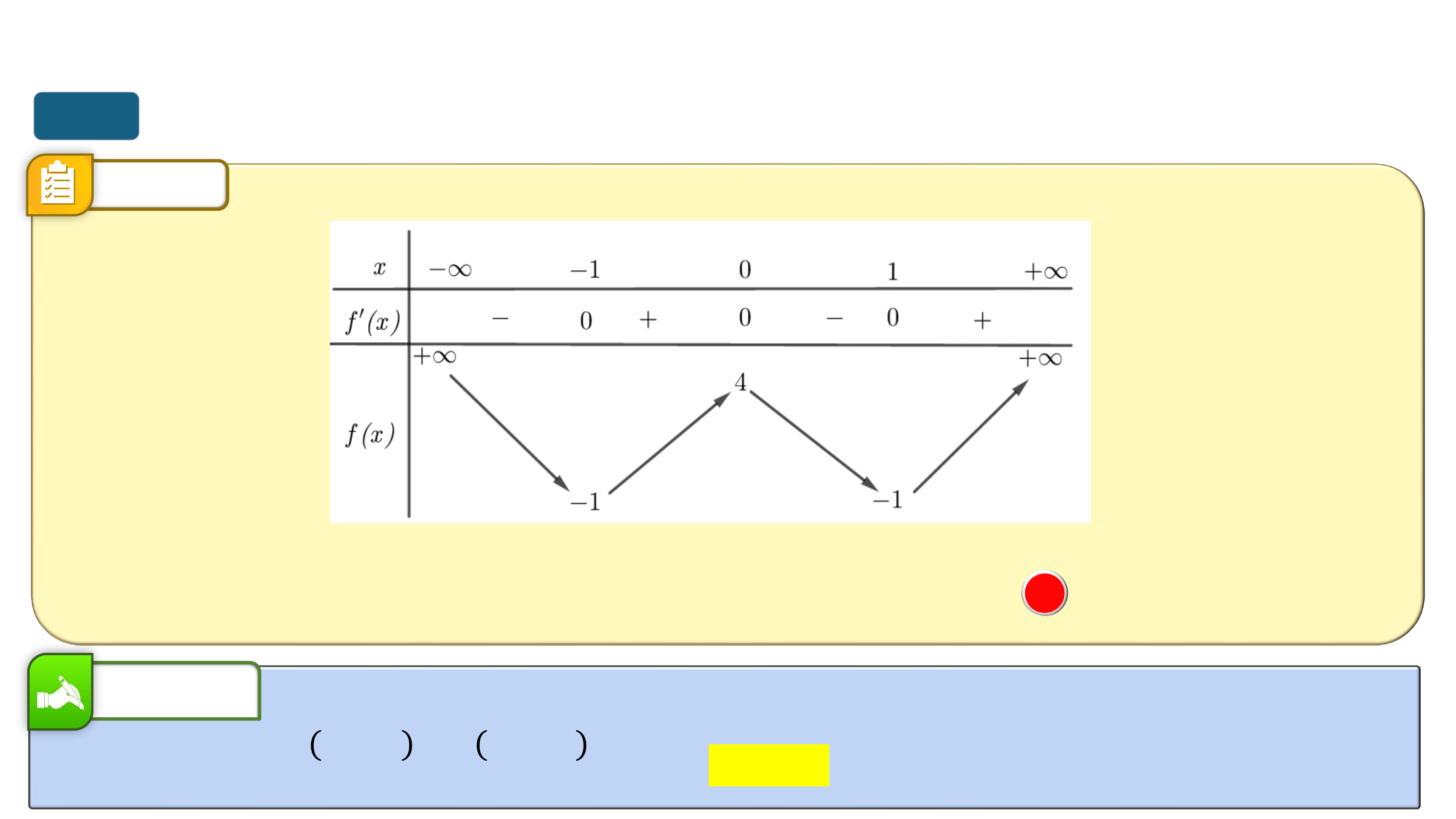
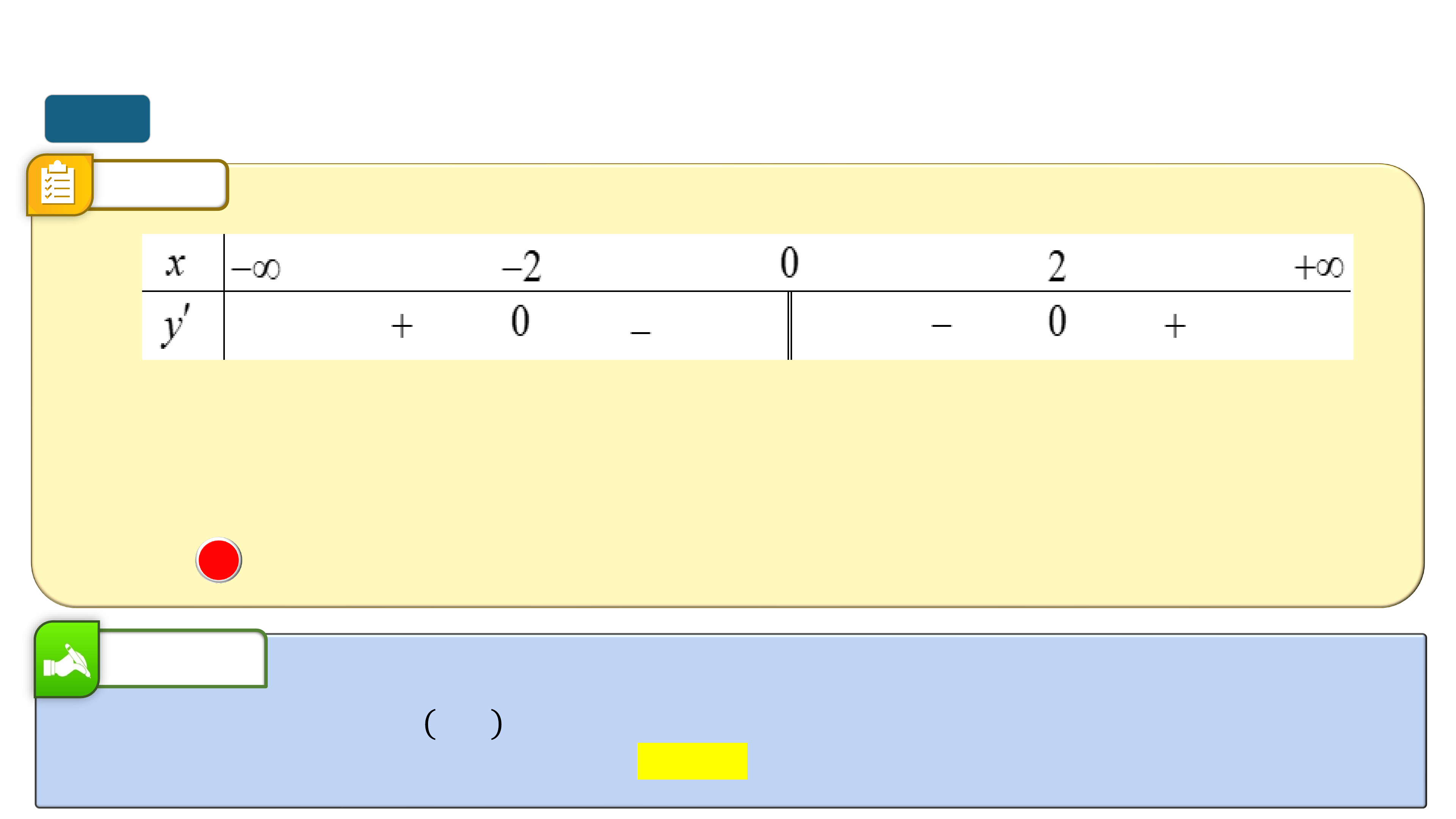
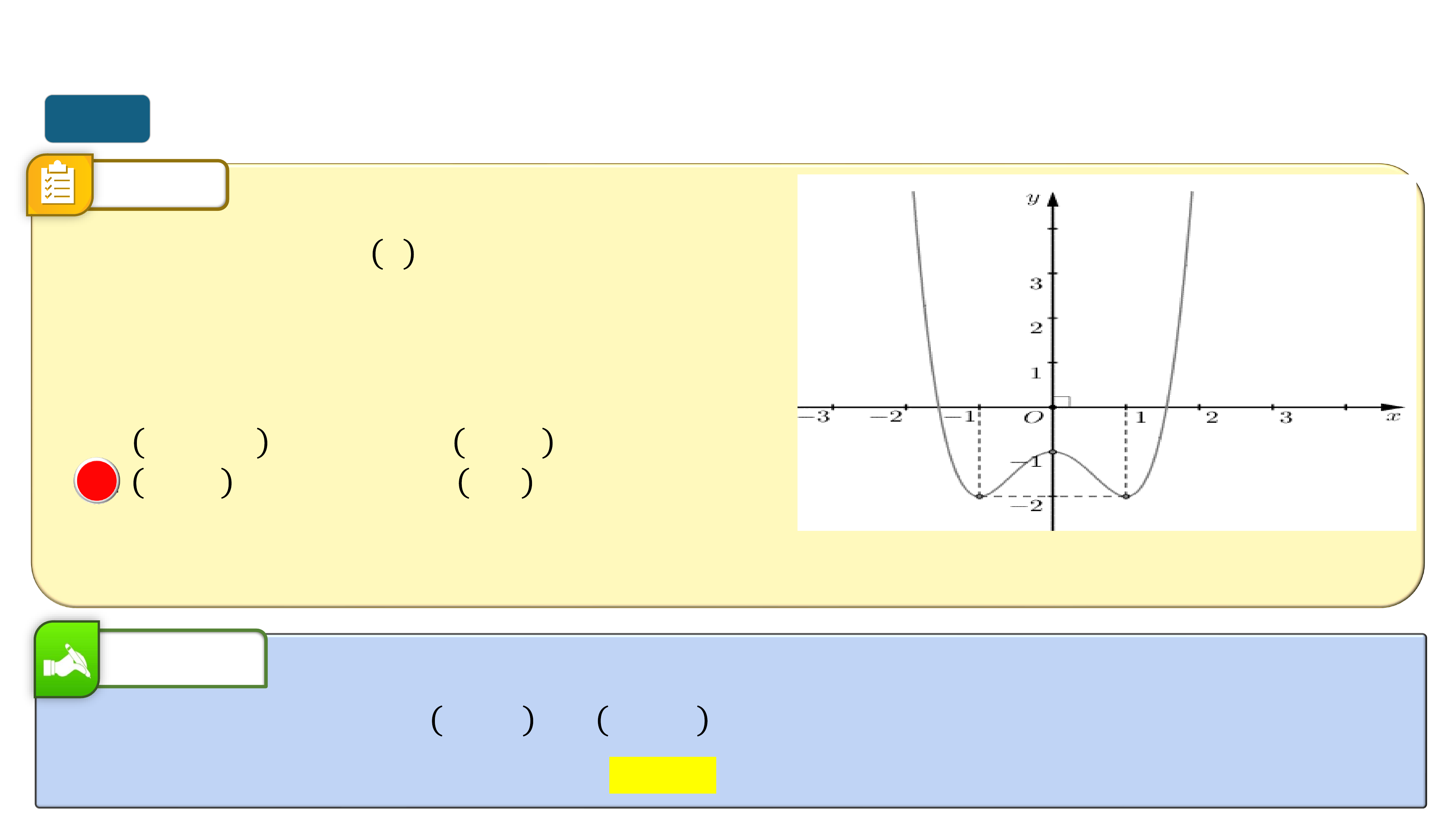
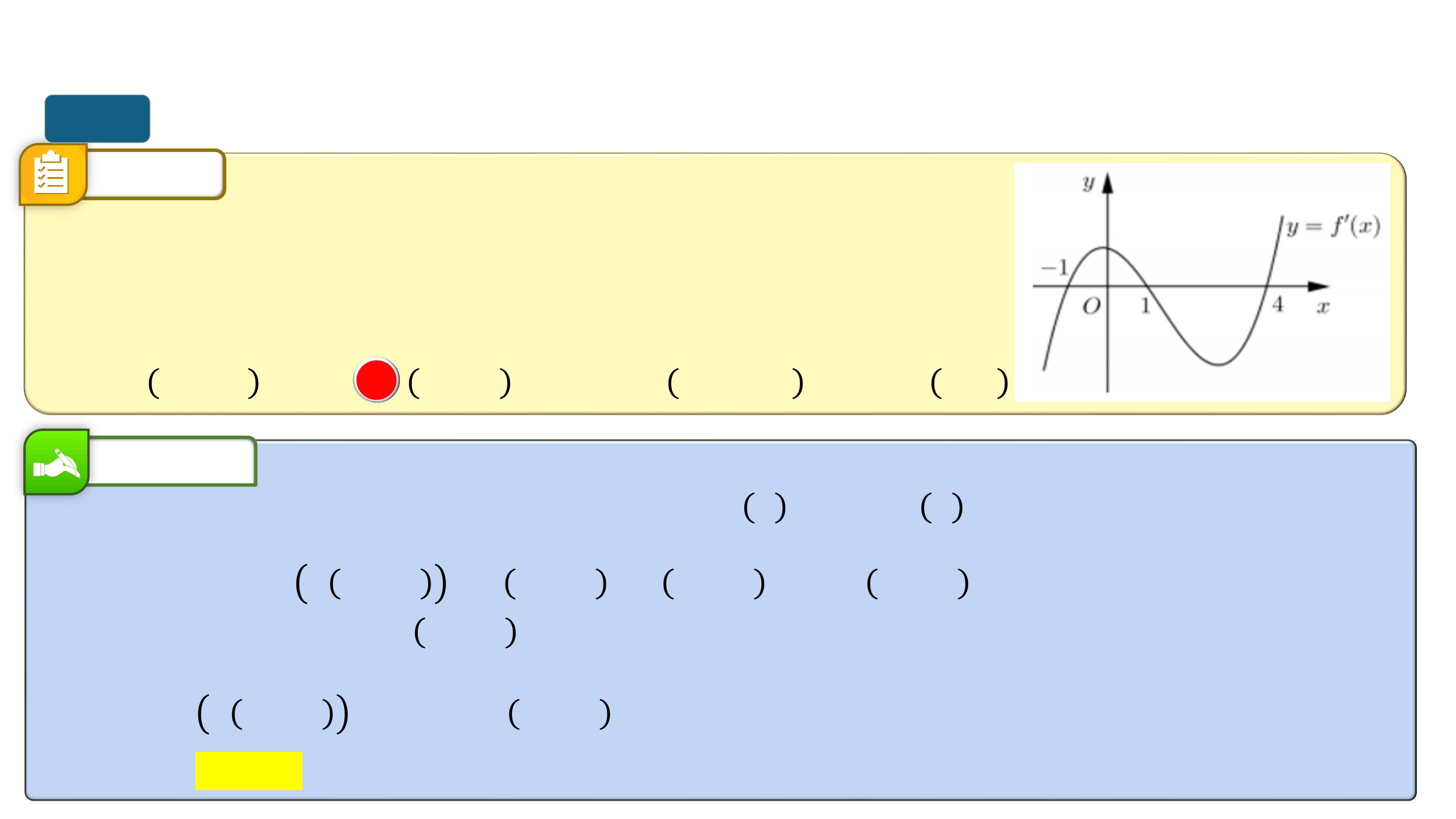
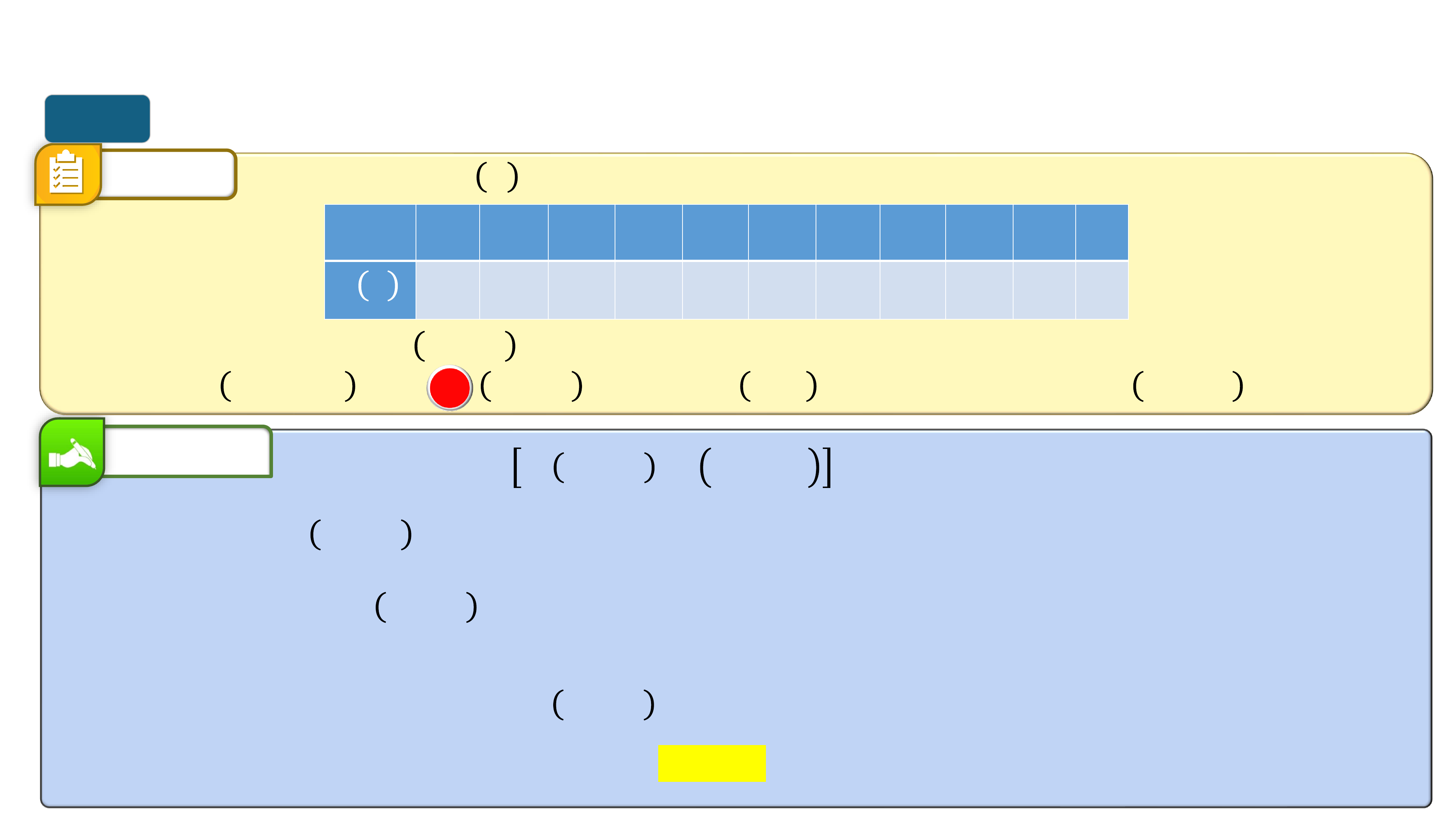
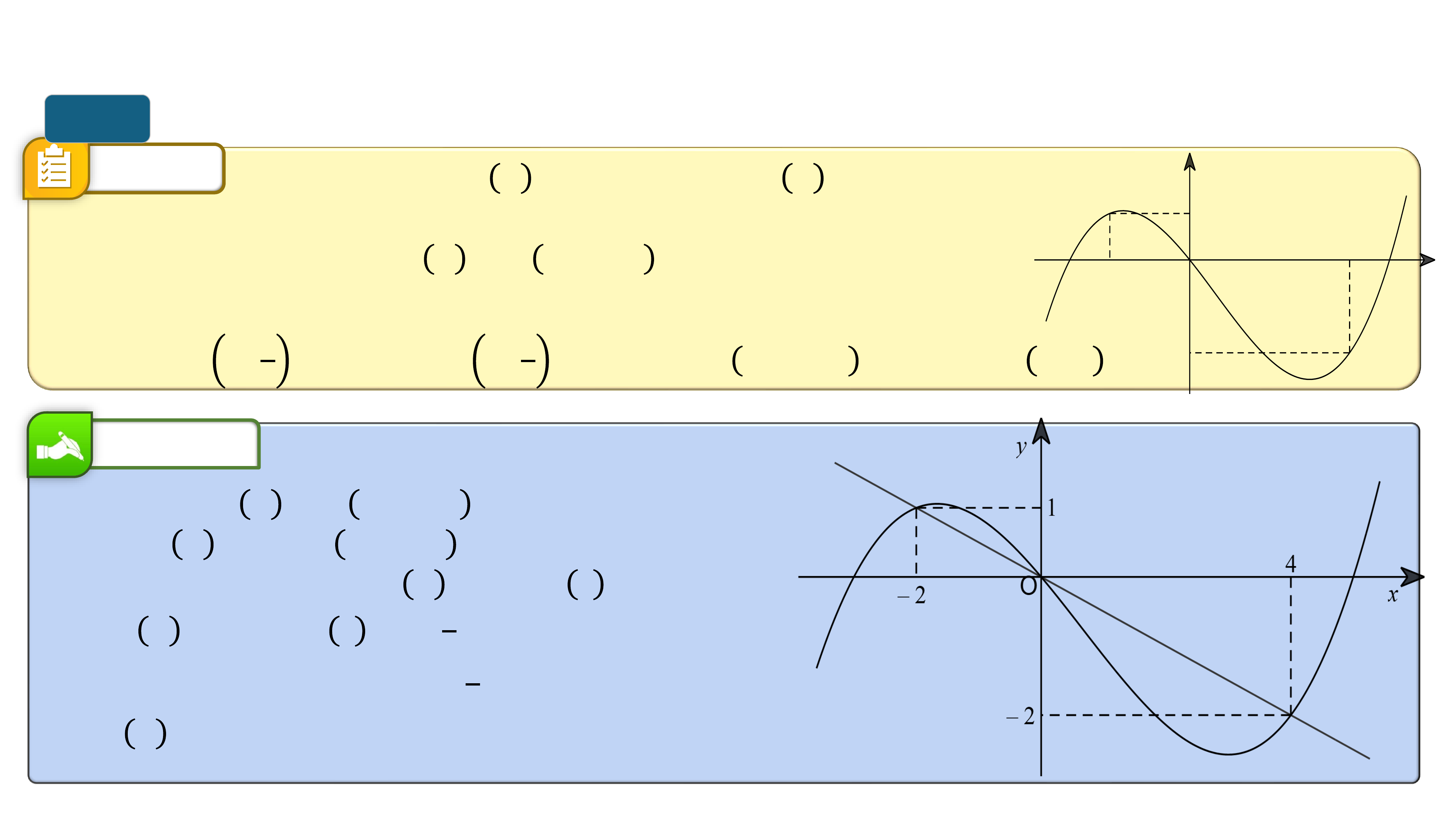
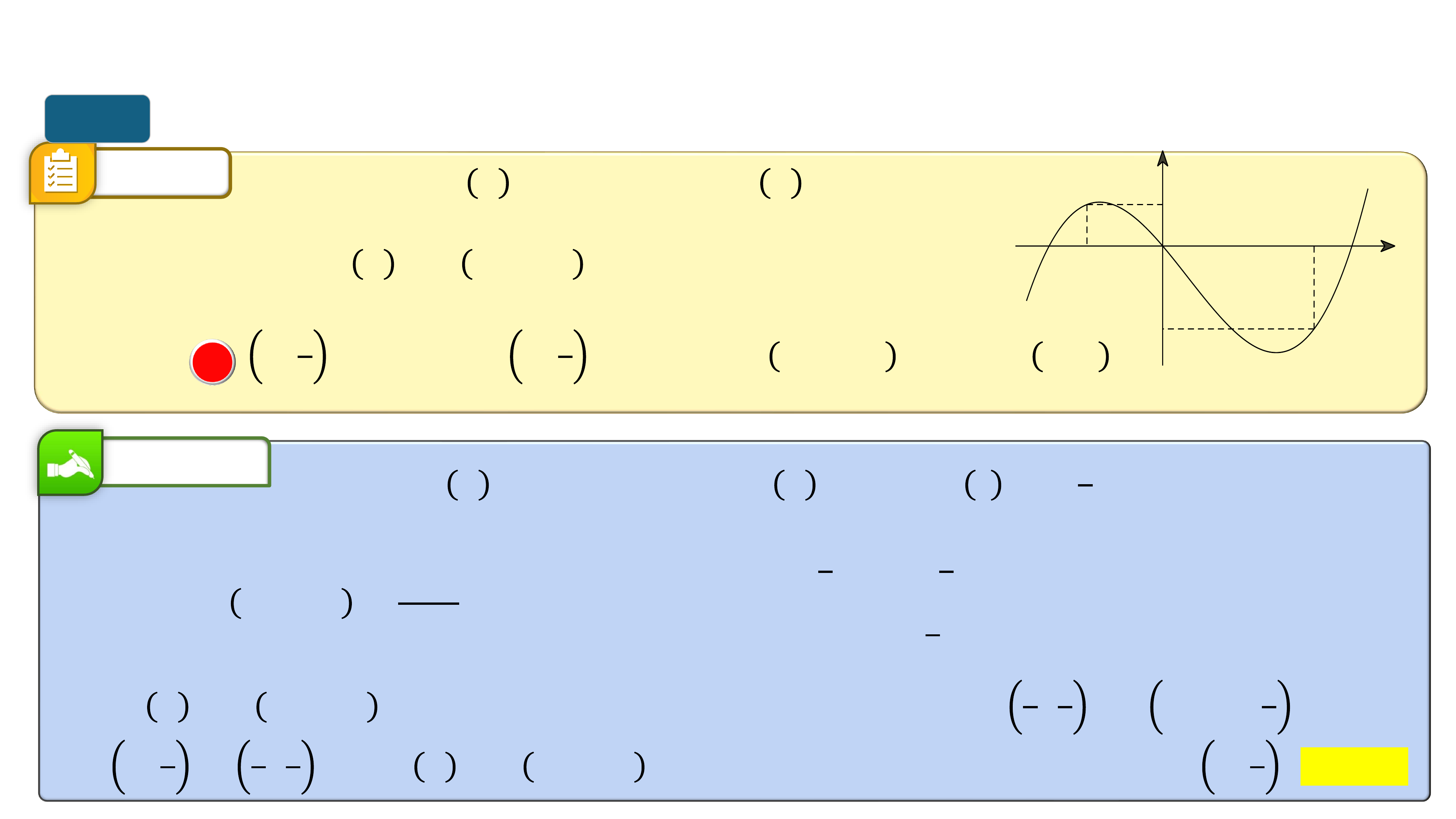
* Trò chơi “Quan sát hình ảnh”. Mỗi nhóm viết lên giấy A4 các khoảng
đồng biến, nghịch biến của của các hàm số tương ứng từ đồ thị sau: I
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1 Nhắc lại định nghĩa Định nghĩa
Giả sử K là một khoảng, một đoạn, một nửa khoảng và ? = ?(?) là một
hàm số xác định trên K. Ta nói:
➢Hàm số được gọi là đồng biến (tăng) trên K nếu ∀? .
?, ?? ∈ ?, ?? < ?? ⇒ ? ?? < ? ??
➢ Hàm số được gọi là nghịch biến (giảm) trên K nếu ∀? .
?, ?? ∈ ?, ?? < ?? ⇒ ? ?? > ? ??
➢ Hàm số đồng biến, nghịch biến trên khoảng K được gọi chung là đơn
điệu trên khoảng K. I
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1 Nhắc lại định nghĩa Chú ý
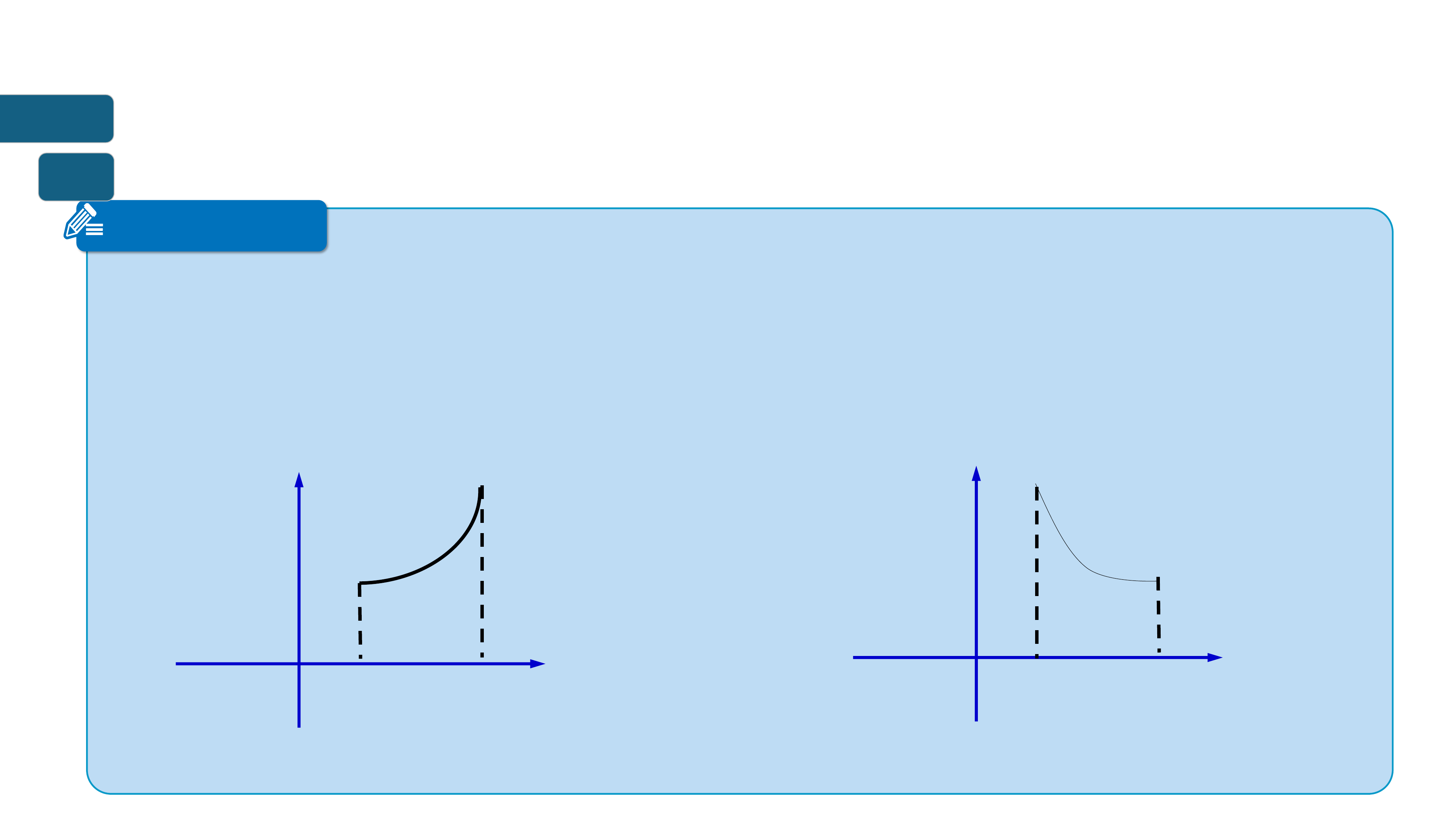
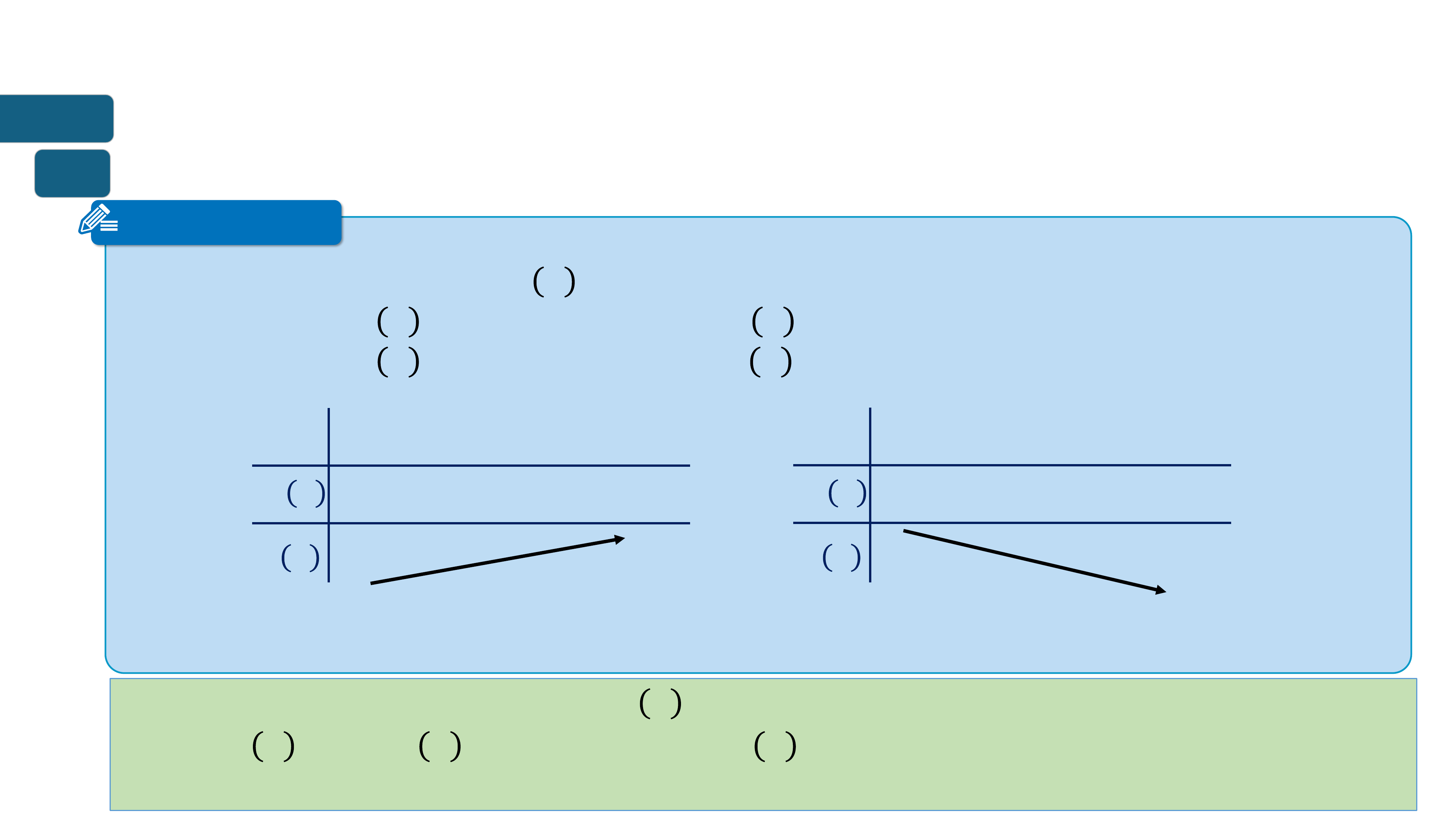
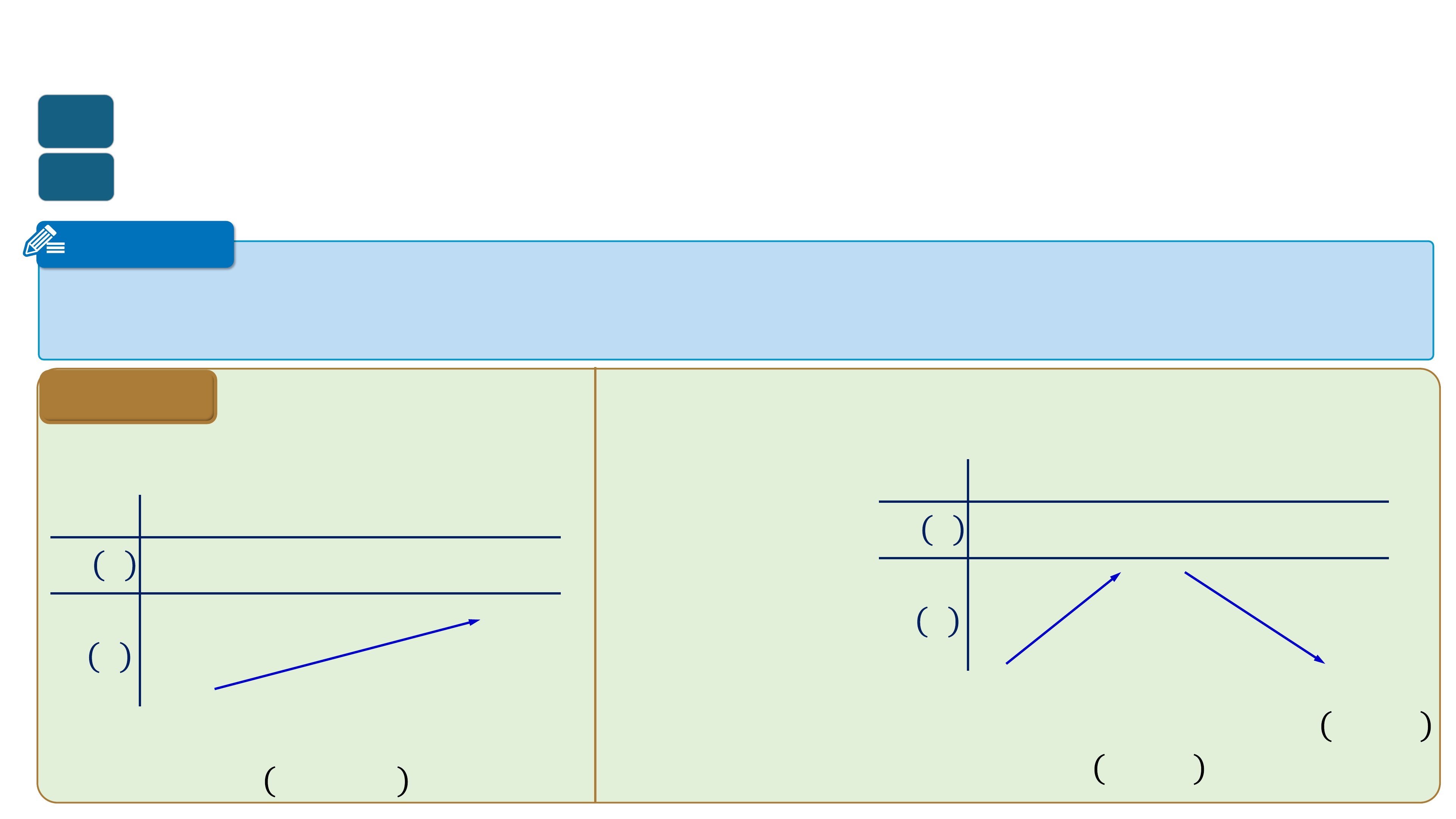
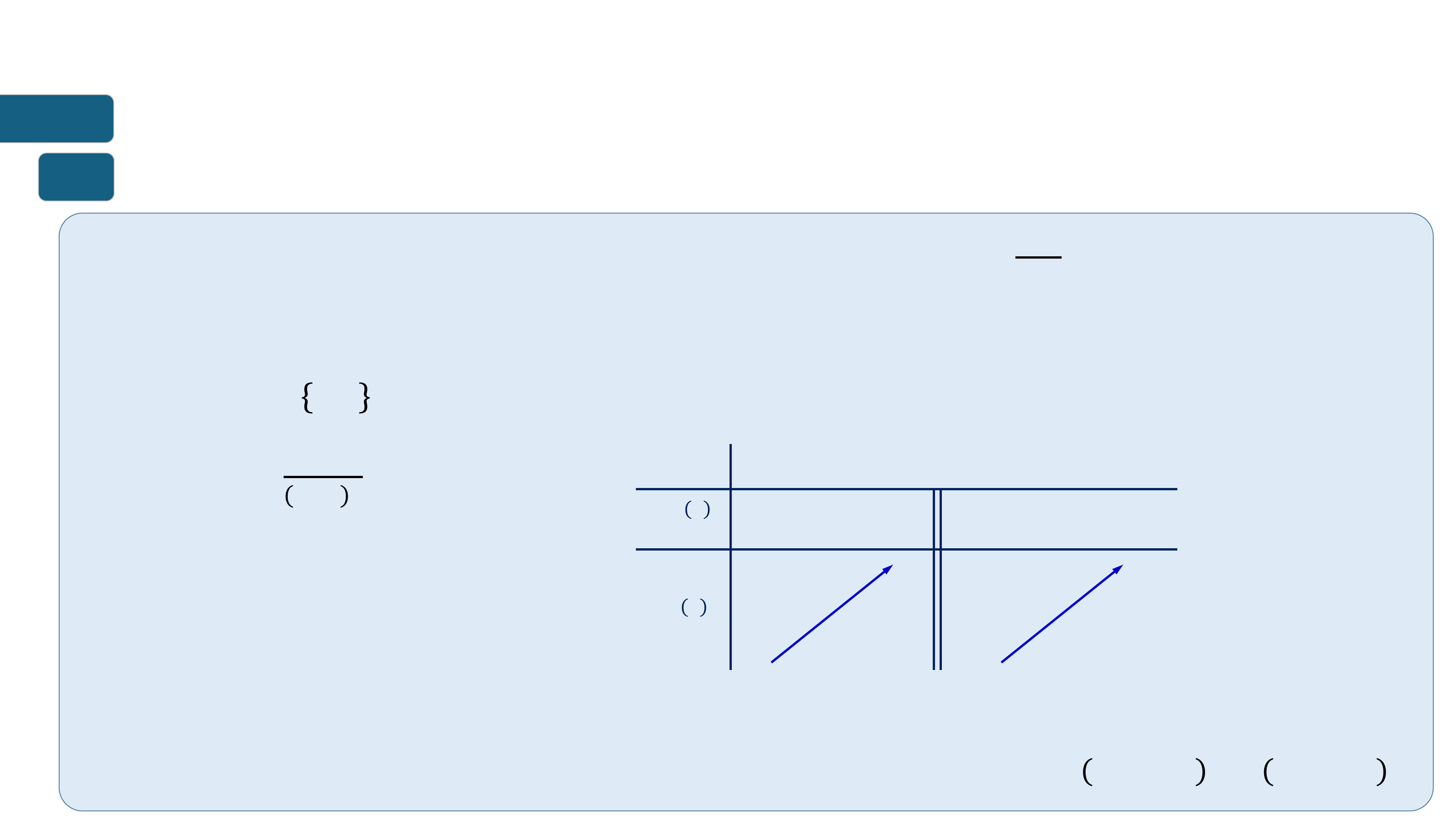
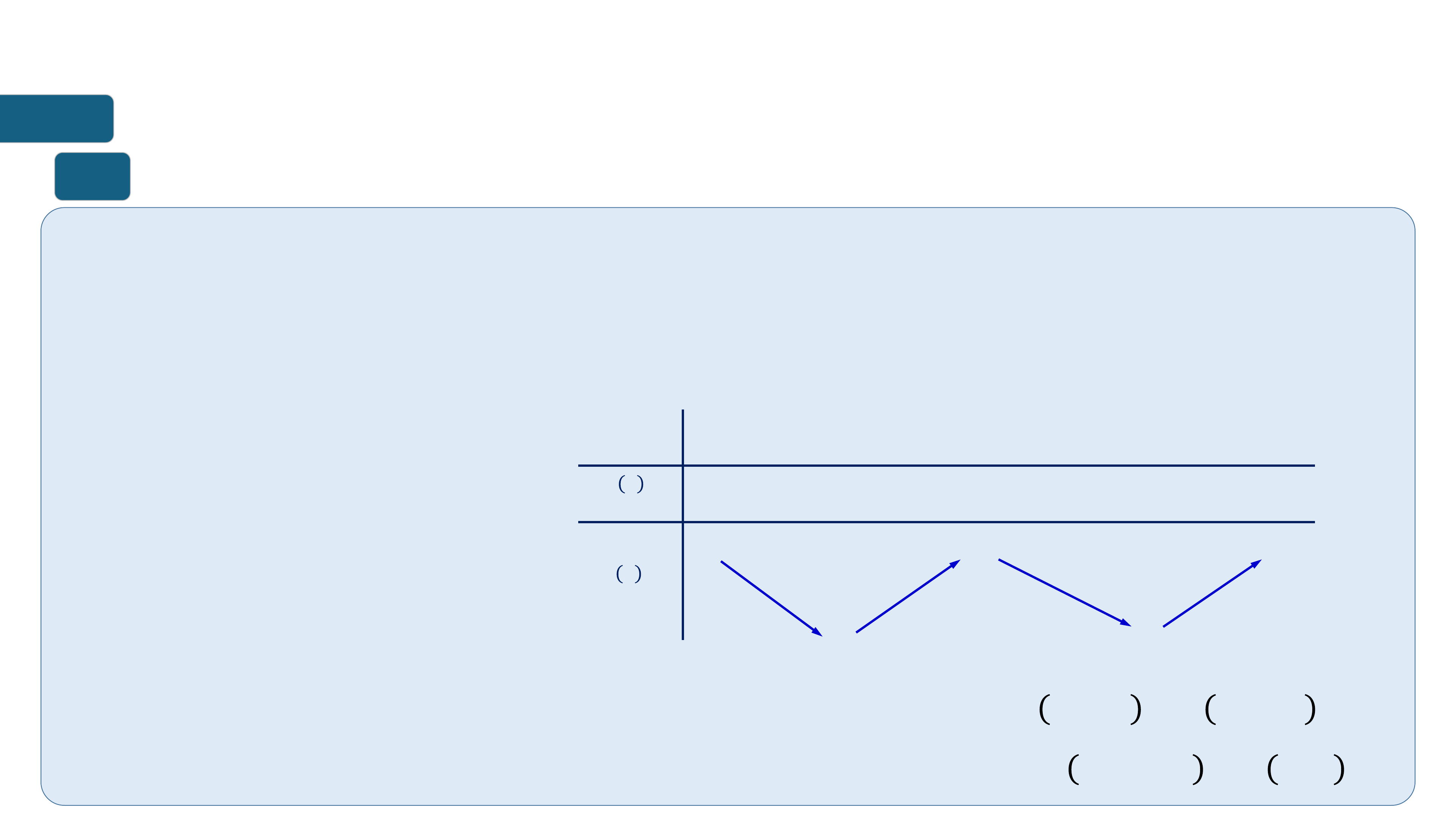
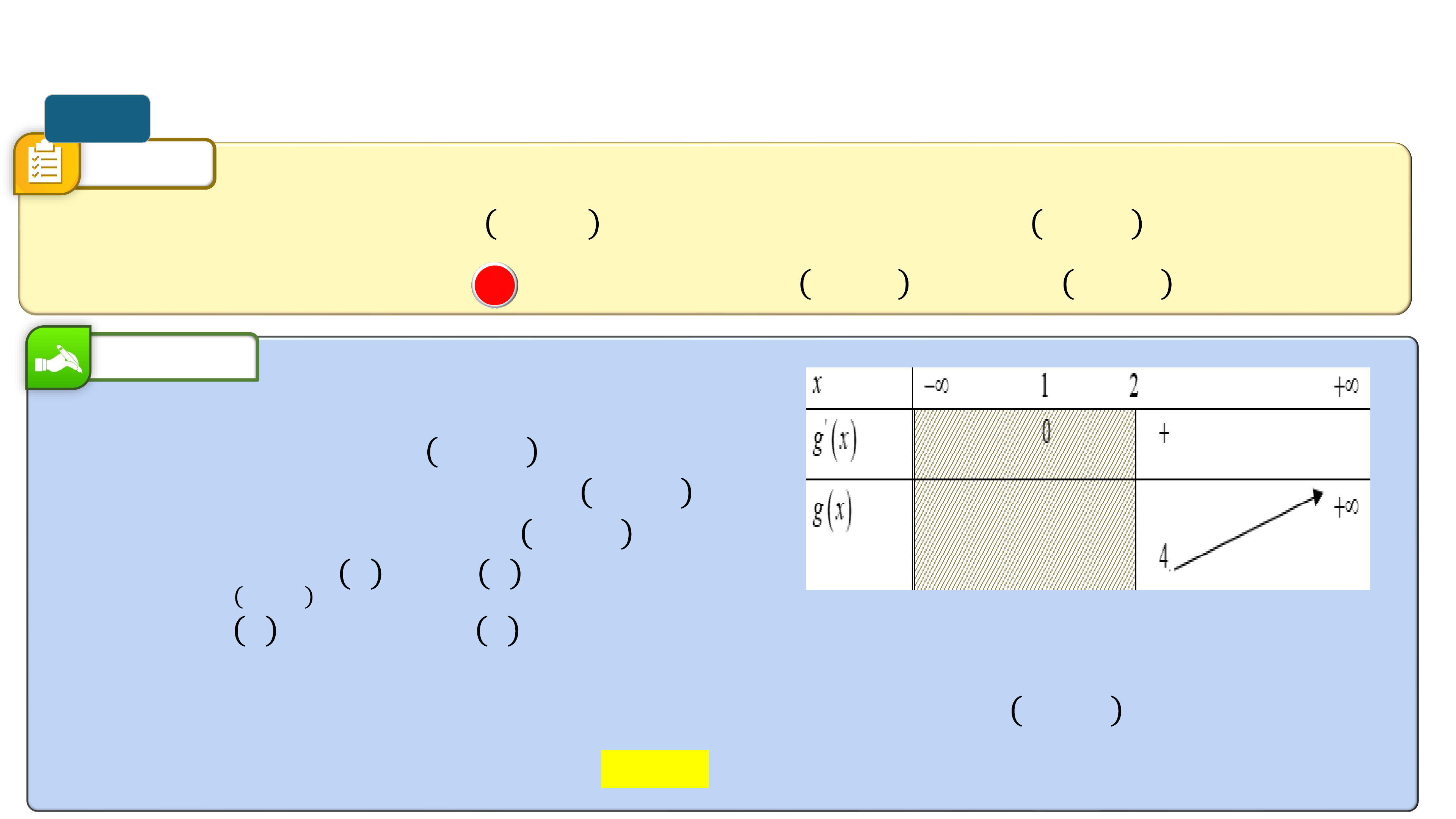
➢ Hàm số đồng biến trên khoảng K thì đồ thị đi lên từ trái sang phải.
➢ Hàm số nghịch biến trên khoảng K thì đồ thị đi xuống từ trái sang phải. ? ? ? = ?(?) ? = ?(?) ? ? ? ? ? ? ? ?
Hàm số đồng biến trên (?; ?)
Hàm số nghịch biến trên (a;b)
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25