LỚP HÌNH HỌC BÀI 1
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1) 12 Chương III HÌNH HỌC
Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
BÀI 1: HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1) I
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
II BIỂU THỨC TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ LỚP HÌNH HỌC BÀI 1
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1) 12 Chương III I.
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
1. Hệ tọa độ trong không gian Định nghĩa
Trong không gian, xét ba trục tọa độ ??; ??; ?? vuông
góc với nhau từng đôi một và chung một điểm gốc ?.
Gọi ?, ?, ? là các vectơ đơn vị tương ứng trên các trục
??; ??; ??. Hệ ba trục như vậy gọi là hệ trục tọa độ
vuông góc trong không gian. Chú ý
?2 = ?2 = ?2 = 1 và ?. ? = ?. ? = ?. ? = 0. LỚP HÌNH HỌC BÀI 1
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1) 12 Chương III I.
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
2. Tọa độ của điểm Định nghĩa
Trong không gian ????, với bộ ba số ?; ?; ? ta có một điểm
? duy nhất thỏa mãn hệ thức ?? = ? ? + ? ? + ??. Ta gọi bộ
ba số ?; ?; ? đó là tọa độ của điểm ? và viết ? ?; ?; ? .
3. Tọa độ của vectơ Định nghĩa
Trong không gian ????, cho vectơ
?. Khi đó luôn tồn tại duy nhất bộ ba số ?; ?; ? sao cho
? = ? ? + ? ? + ??. Ta gọi bộ ba số ?; ?; ? đó là tọa độ của vectơ ?. Nhận xét
Trong hệ tọa độ ????, tọa độ của điểm ? chính là tọa độ của vectơ ??. LỚP HÌNH HỌC BÀI 1
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1) 12 Chương III I.
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ Ví dụ 1
Trong hệ trục tọa độ ????, cho ? = 2 ? − 3 ? + 4?, ?? = 1; −4; 2 , ?? = ? −
3?. Xác định tọa độ của vectơ ?, điểm ?, điểm ?. Bài giải
? = 2 ? − 3 ? + 4? ⇔ ? = 2; −3; 4 .
?? = 1; −4; 2 ⇔ ? 1; −4; 2 .
?? = ? − 3? ⇔ ?? = 1; 0; −3 ⇔ ? 1; 0; −3 .
Giáo án Powerpoint Hệ tọa độ trong không gian Toán 12 Hình học
875
438 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Bộ bài giảng điện tử Toán 12 Hình học được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Bộ bài giảng powerpoint Toán 12 Hình học bao gồm đầy đủ các bài giảng trong cả năm học. Bộ bài giảng được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng phần học và bám sát chương trình Sách giáo khoa Toán 12 Hình học.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(875 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 12
Xem thêmTài liệu bộ mới nhất
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
HÌNH HỌC
Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
I
BIỂU THỨC TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
II
BÀI 1: HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
I.
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
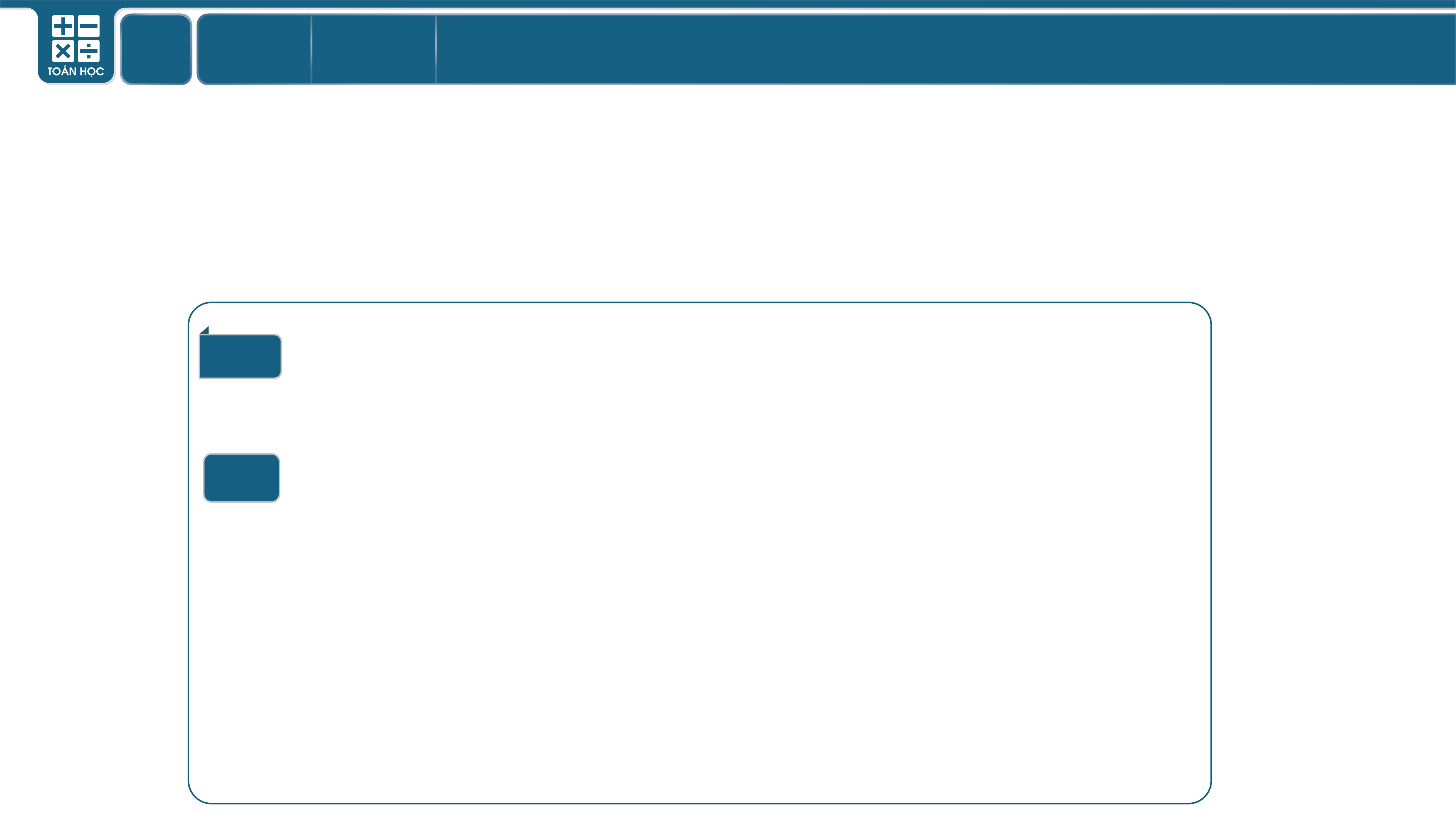
Trong không gian, xét ba trục tọa độ vuông
góc với nhau từng đôi một và chung một điểm gốc .
Gọi là các vectơ đơn vị tương ứng trên các trục
. Hệ ba trục như vậy gọi là hệ trục tọa độ
vuông góc trong không gian.
Định nghĩa
Hệ tọa độ trong không gian
1.
Chú ý
và .
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
I.
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
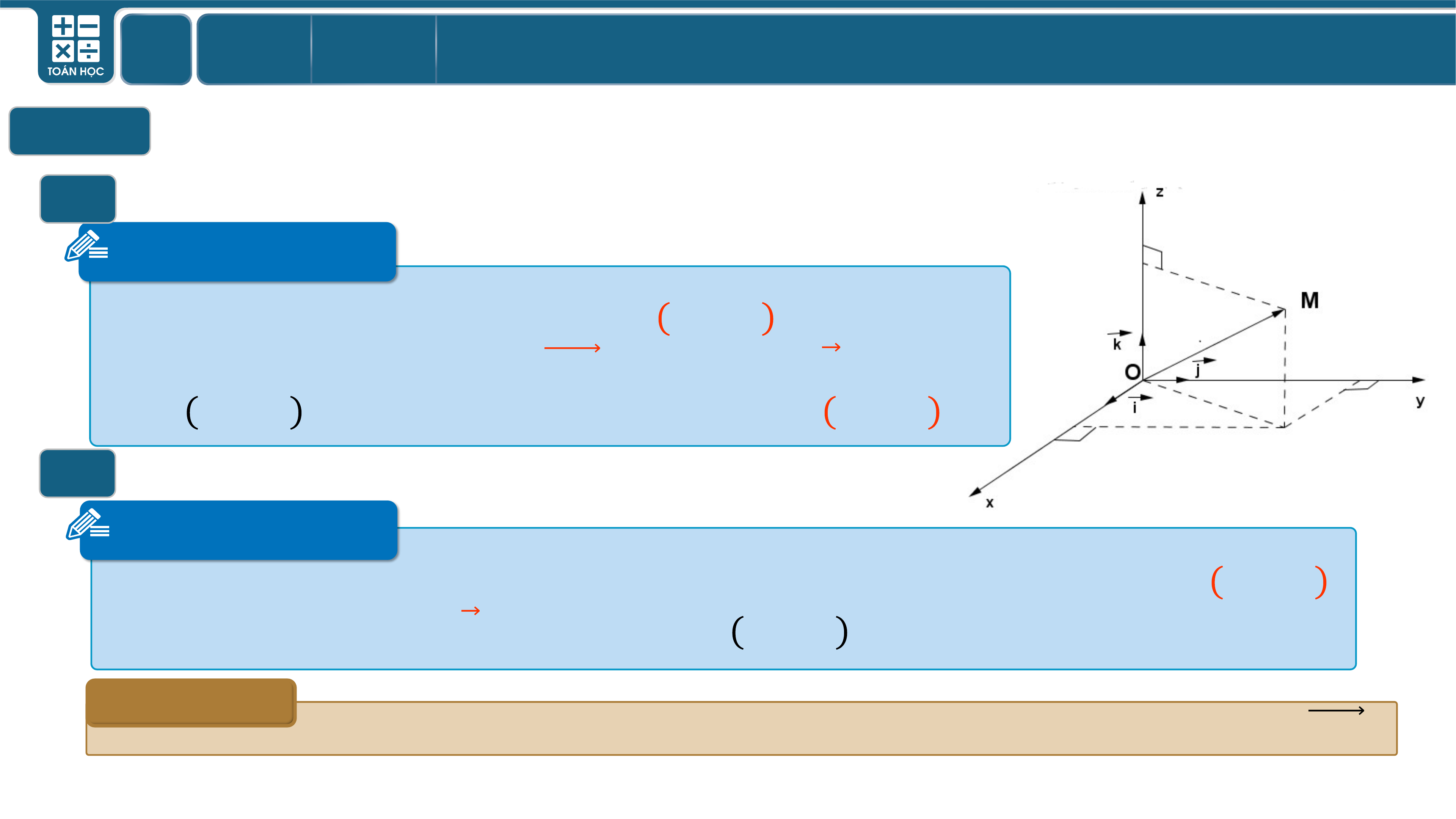
Trong không gian , với bộ ba số ta có một điểm
duy nhất thỏa mãn hệ thức . Ta gọi bộ
ba số đó là tọa độ của điểm và viết .
Định nghĩa
Tọa độ của điểm
2.
Trong không gian , cho vectơ . Khi đó luôn tồn tại duy nhất bộ ba số
sao cho . Ta gọi bộ ba số đó là tọa độ của vectơ .
Định nghĩa
Tọa độ của vectơ
3.
Nhận xét
Trong hệ tọa độ , tọa độ của điểm chính là tọa độ của vectơ .

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
I.
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
Ví dụ 1
Trong hệ trục tọa độ , cho ,
Xác định tọa độ của vectơ , điểm , điểm
Bài giải
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
II.
BIỂU THỨC TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
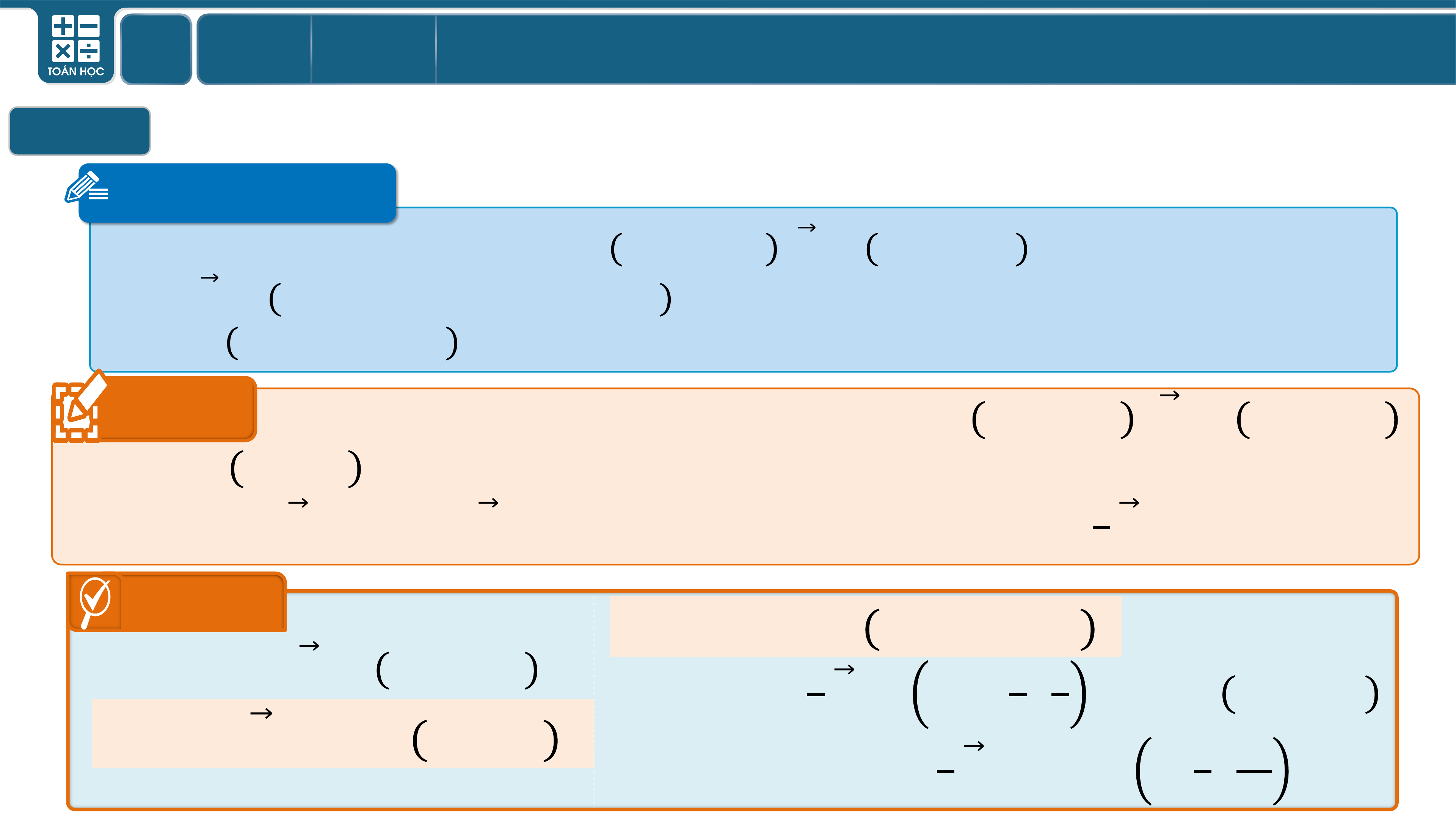
Trong không gian , cho
. Ta có:
Định lý
Ví dụ 2
Trong không gian , cho ba vectơ ,
và . Xác định tọa độ của các vectơ
a) b) c) d)
.
Bài giải
a) .
b) .
c) .
d) Ta có
, .
Khi đó:

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
II.
BIỂU THỨC TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
Trong không gian , cho
,
;
. Ta có:
Hệ quả
• vectơ
cùng phương
•
Tọa độ trung điểm I của đoạn thẳng AB:
Tọa độ trọng tâm G của tam giác ABC:

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
II.
BIỂU THỨC TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
Ví dụ 2
Trong không gian , cho ba điểm ,
và .
a) Xác định tọa độ của các vectơ .
b) Chứng minh ba điểm tạo thành một tam giác.
c) Xác định tọa độ trung điểm của đoạn thẳng .
d) Xác định tọa độ trọng tâm của tam giác .
Bài giải
a) .
b) Ta có
. Suy ra không cùng phương.
Hay ba điểm tạo thành một tam giác.

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
II.
BIỂU THỨC TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
Ví dụ 2
Trong không gian , cho ba điểm ,
và .
a) Xác định tọa độ của các vectơ .
b) Chứng minh ba điểm tạo thành một tam giác.
c) Xác định tọa độ trung điểm của đoạn thẳng .
d) Xác định tọa độ trọng tâm của tam giác .
Bài giải
c) Gọi
. là trung điểm của đoạn thẳng
. Vậy
.
là trọng tâm của tam giác
Vậy

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
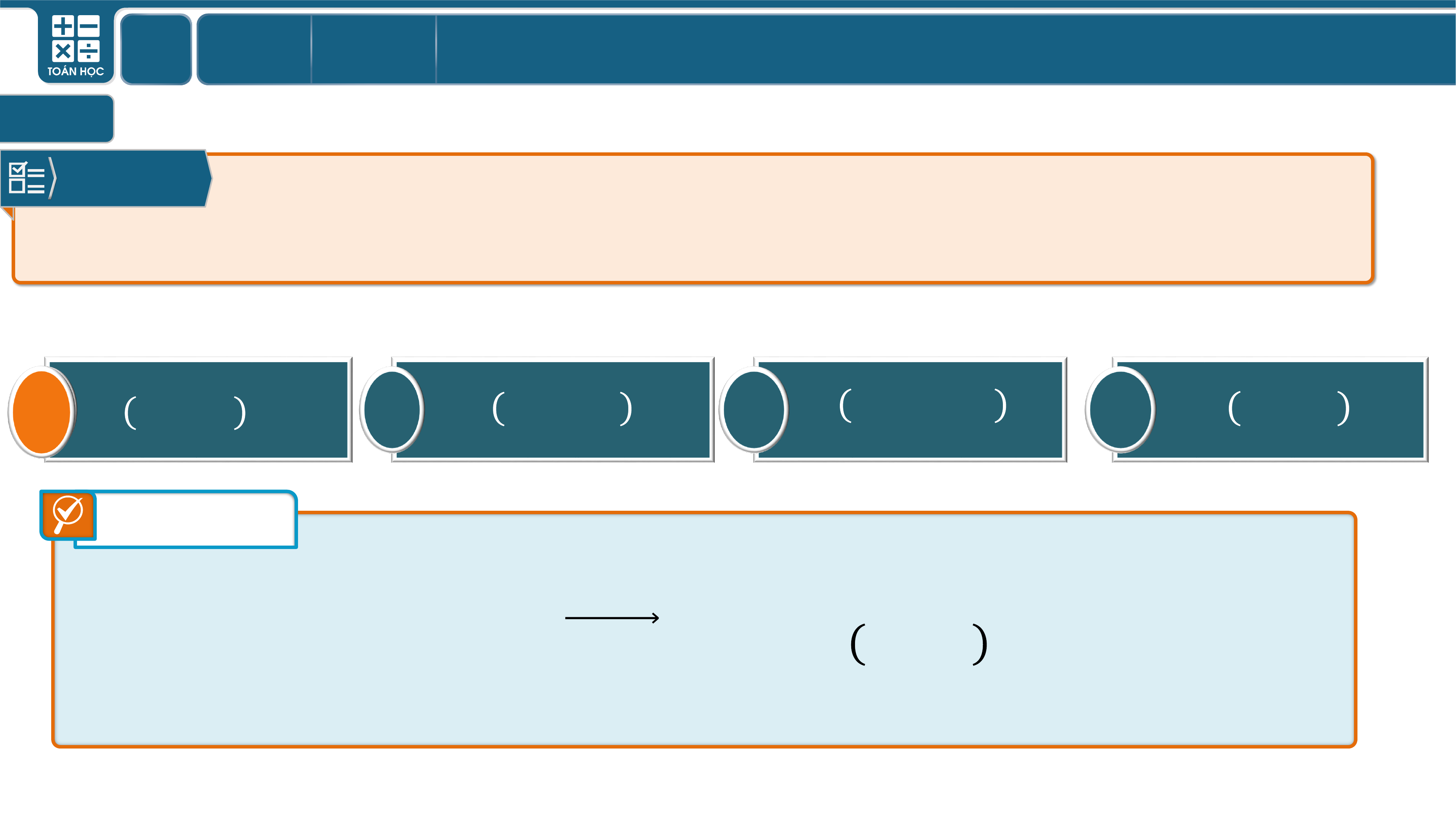
Câu 1
Trong không gian với hệ trục tọa độ
cho . Tọa độ của vectơ là
B C DA
D
.
Hướng dẫn
Ta có
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
Câu 2
Trong không gian , cho điểm M(8;9;10). Tìm tọa độ hình
chiếu vuông góc của điểm lên trục hoành.
B C DA
A
.
Hướng dẫn
Gọi là hình chiếu vuông góc của lên trục hoành.
Suy ra M’ (a;0;0) ϵ Ox và
.
Vậy M’ (8;0;0).

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
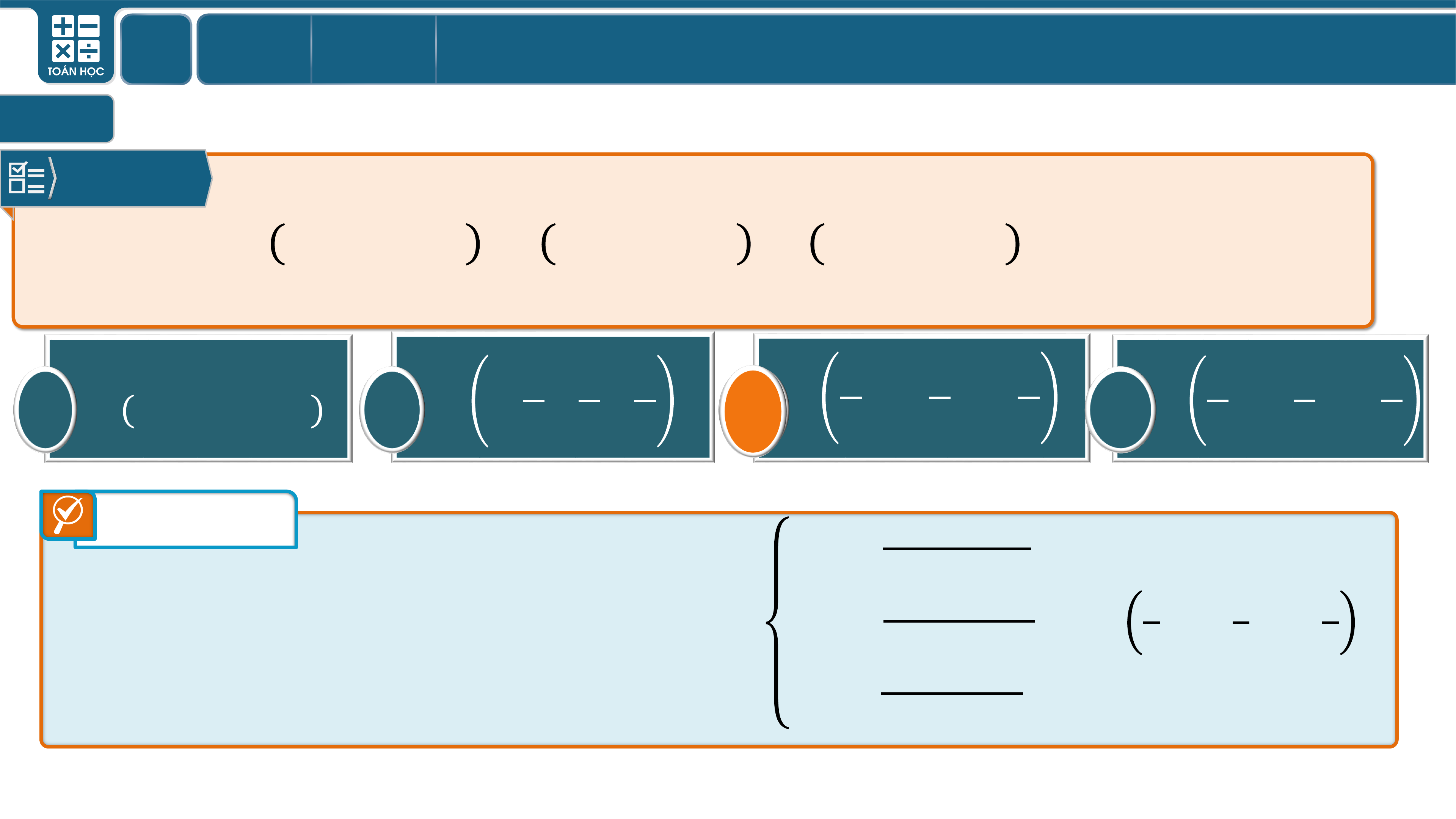
Câu 3
Trong không gian , cho hai điểm và
. Tọa độ trung điểm của đoạn thẳng là
B C DA
C
.
Hướng dẫn
Tọa độ trung điểm của đoạn thẳng là
.
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
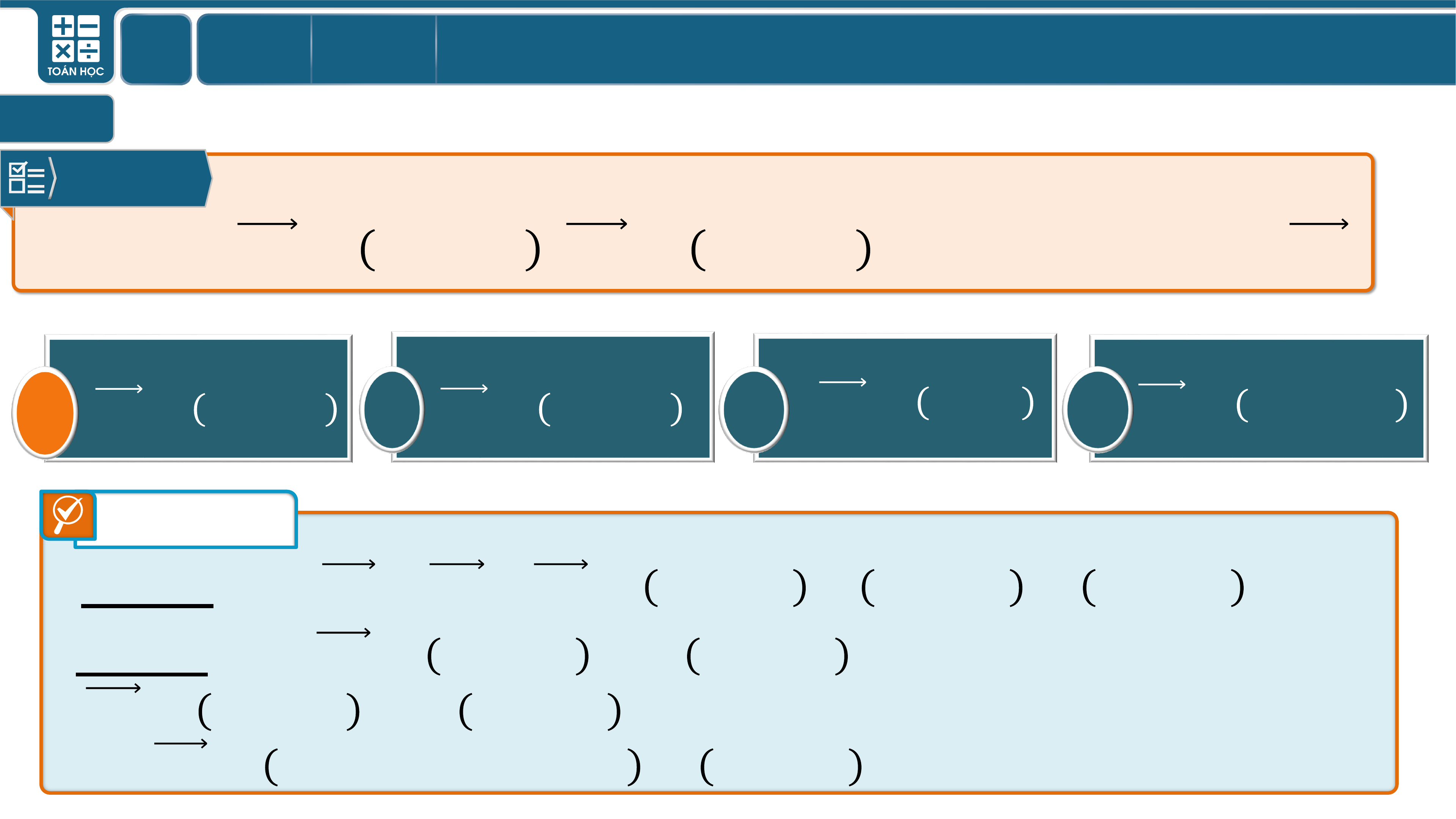
Câu 4
Trong không gian với hệ tọa độ , cho ba điểm
, , . Tìm tọa độ trọng
tâm của tam giác
B C DA
C
.
Hướng dẫn
Tọa độ trọng tâm của tam giác là
.
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
Câu 5
Trong không gian với hệ tọa độ , cho hai điểm , với
, Tìm tọa độ của vectơ .
B C DA
A
.
Hướng dẫn
Cách 1. Ta có .
Cách 2. Ta có và
.
Vậy .

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
Câu 6
Trong không gian với hệ tọa độ , cho vectơ
. Tìm tọa độ của vectơ , biết
vectơ cùng phương với vectơ .
B C DA
A
.
Hướng dẫn
Vectơ cùng phương với vectơ

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
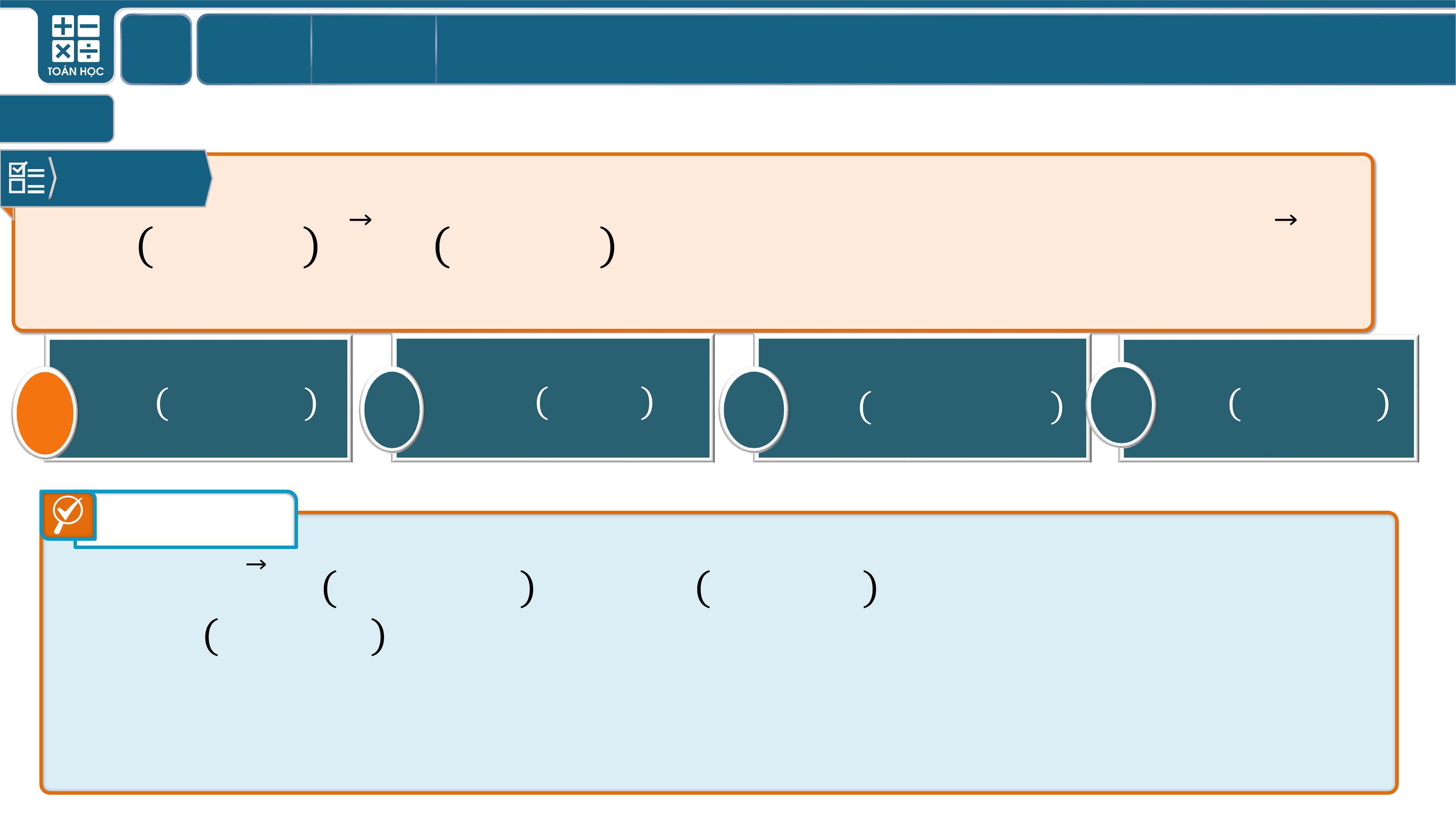
Câu 7
Trong không gian với hệ tọa độ cho hai điểm ,
. Tìm tọa độ điểm thỏa mãn đẳng thức
.
B C DA
A
.
Hướng dẫn
Gọi điểm . Khi đó
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
Câu 8
Trong không gian với hệ tọa độ , cho các vectơ
, . Tìm tọa độ của vectơ .
B C
D
A
A
.
Hướng dẫn
Ta có mà
.

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
Câu 9
Trong không gian với hệ trục toạ độ , cho
, , và .
Đẳng thức nào đúng trong các đẳng thức sau?
.
Hướng dẫn
Đặt với , , .
Khi đó
.
B
A
C
D
C
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
Câu 10
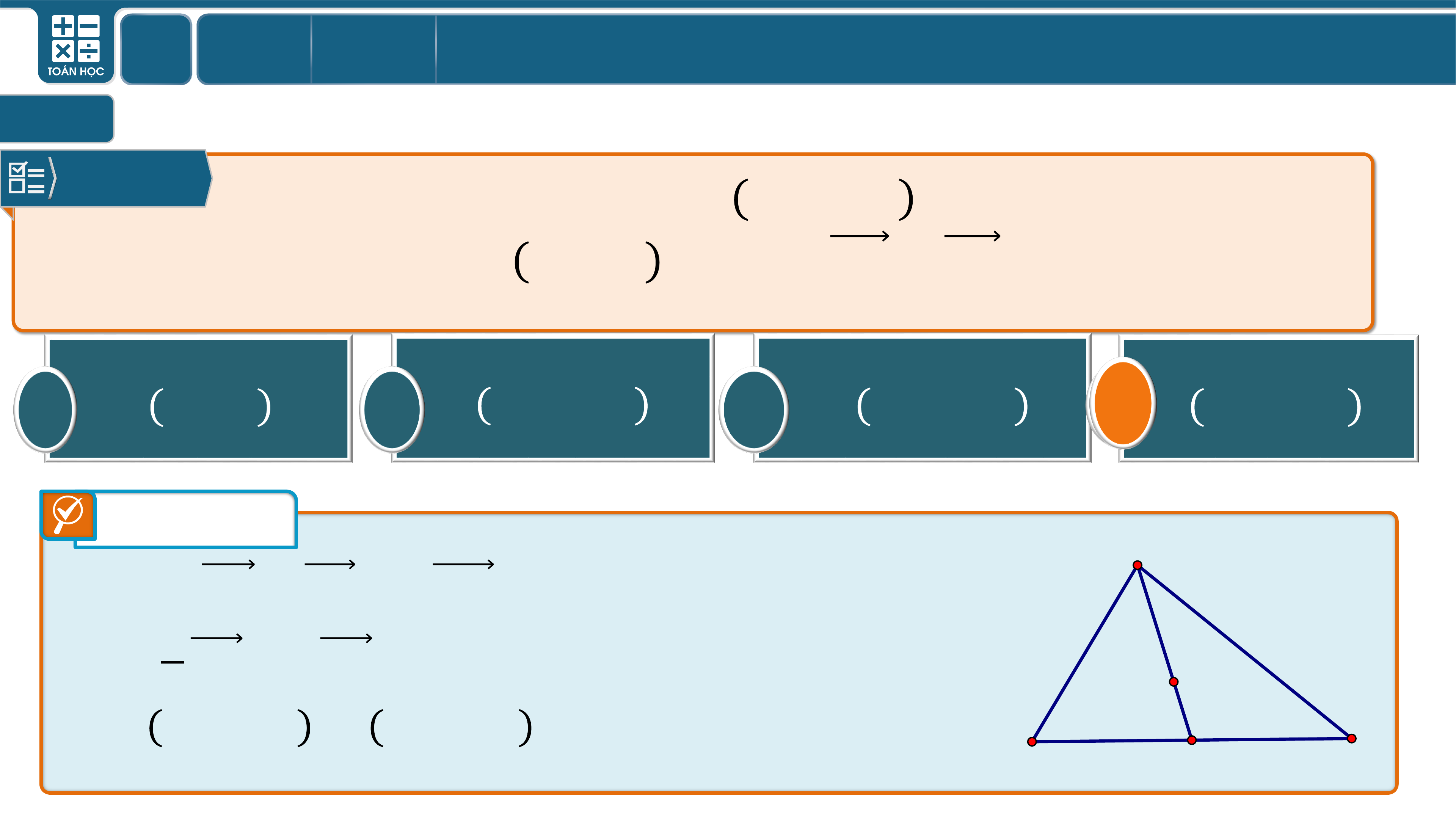
Cho tam giác biết và trọng tâm của
tam giác có toạ độ là . Khi đó có tọa độ là.
B C
D
A
D
0;;9 .
0;9;
0;6;
0; 9;9
Hướng dẫn
Ta có:
.
G
M
A
B
C
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
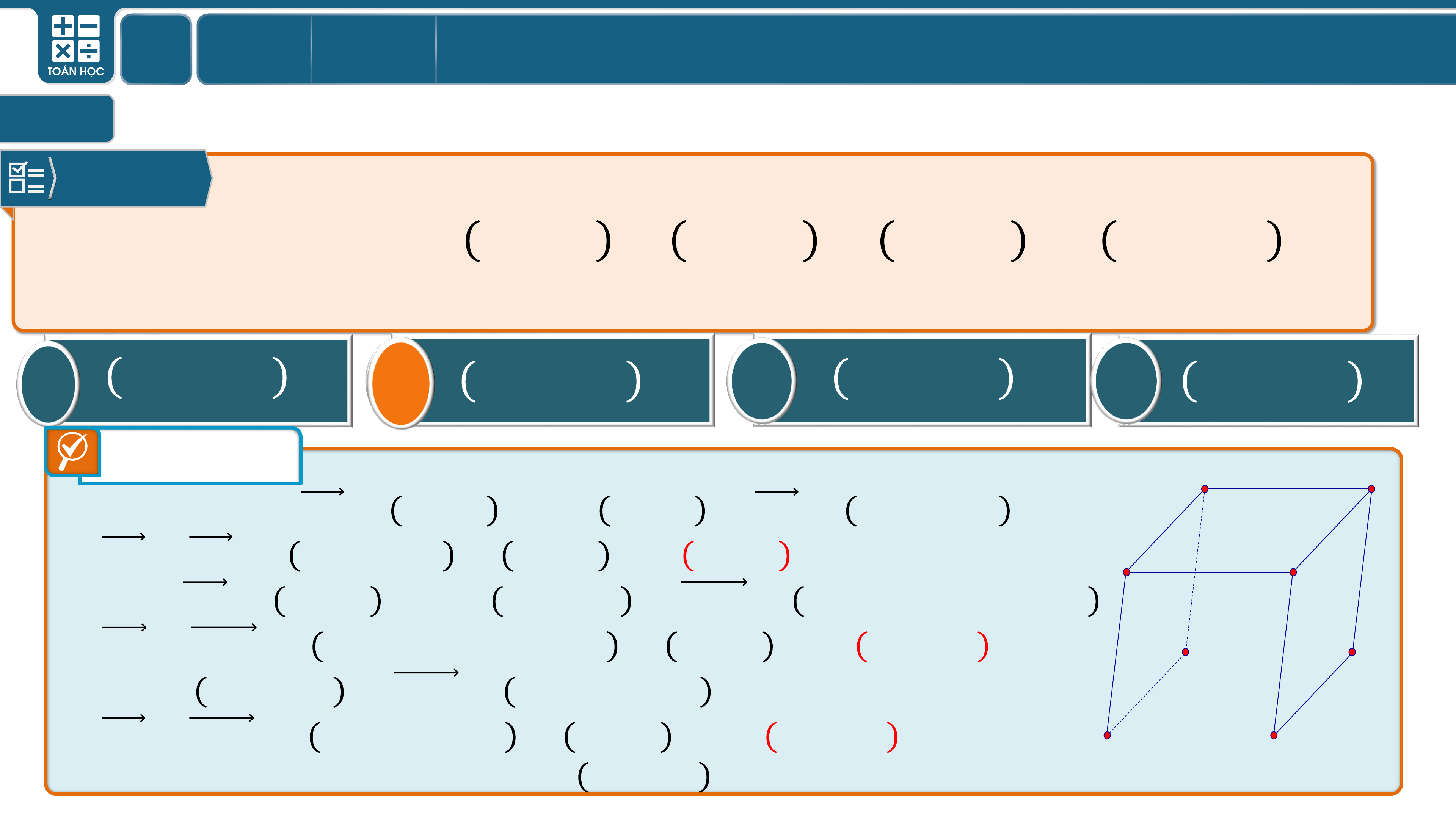
Câu 11
Trong không gian với hệ toạ độ , cho hình hộp
có , , ,
.
Toạ độ trọng tâm tam giác
là
B C D
A
B
.
Hướng dẫn
Cách 1: Ta có . Gọi
Ta có . Gọi
Gọi
là trọng tâm tam giác .
A
B
C
D
A
B
C
D
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BÀI TẬP CỦNG CỐ
.
.
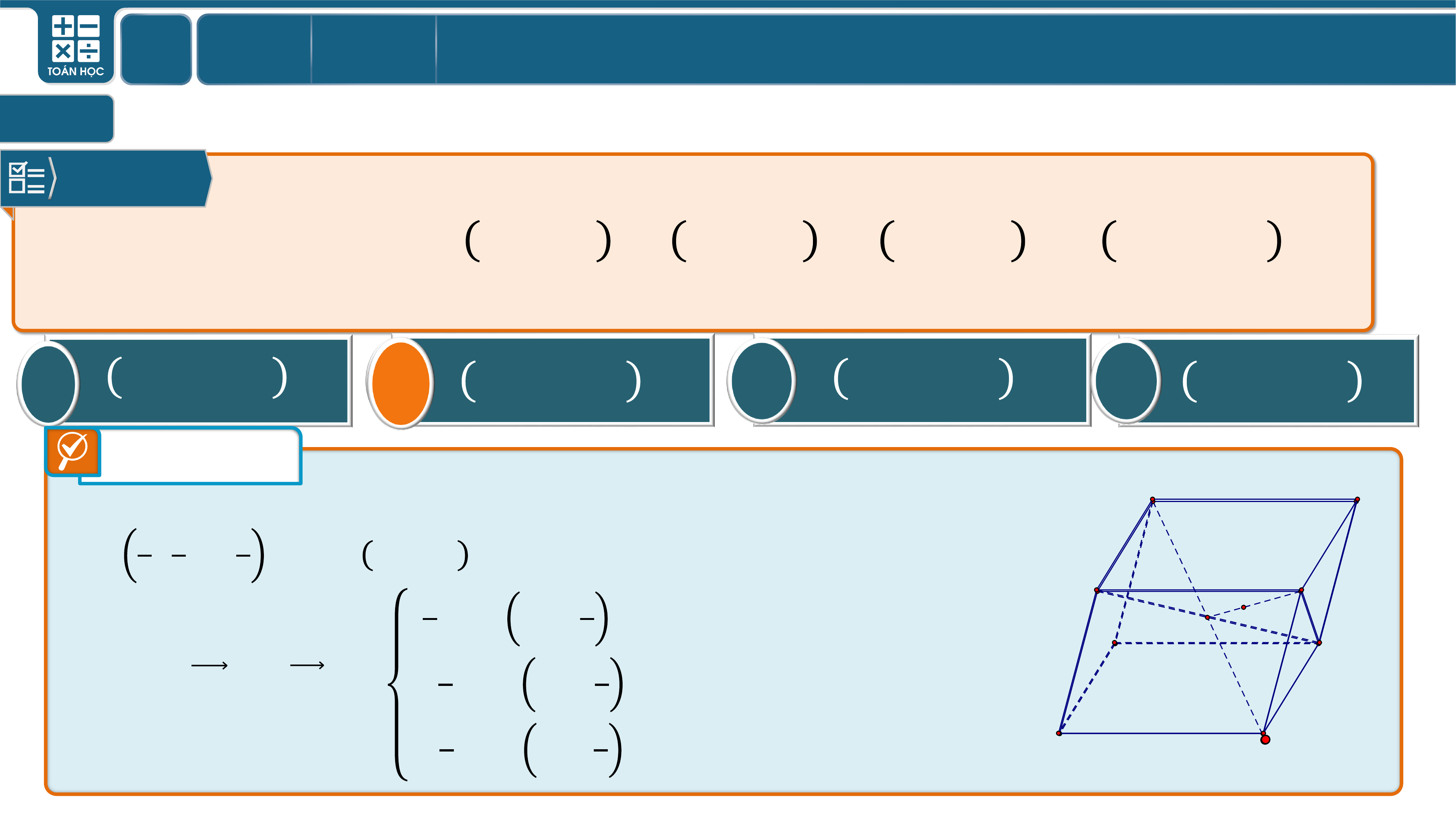
Câu 11
Trong không gian với hệ toạ độ , cho hình hộp
có , , ,
.
Toạ độ trọng tâm tam giác
là
B C D
A
B
.
Hướng dẫn
Cách 2: Gọi là trung điểm của đoạn thẳng
.Ta có
.Gọi là trọng tâm tam giác
.
Ta có:
.
I
B'
B
A'
C'
D'
A
C
D
G
B'
B
D
C
A
D'
C'
A'
HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
TỌA ĐỘ CỦA
VECTƠ
Trong không gian , cho vectơ . Khi đó luôn tồn tại duy nhất
bộ ba số sao cho . Ta gọi bộ ba số
đó là tọa độ của vectơ .
TỌA ĐỘ CỦA
ĐIỂM
TỌA ĐỘ CỦA
ĐIỂM
Trong hệ tọa độ , tọa độ của điểm chính là
tọa độ của vectơ .
Ta có:

HỆ TỌA ĐỘ TRONG KHÔNG GIAN (tiết 1)
HÌNH HỌC
LỚP
12
BÀI 1
Chương III
BIỂU THỨC TỌA ĐỘ
CỦA ĐIỂM VÀ CỦA
VECTƠ
Trong không gian , cho
.
cùng phương
Tọa độ trung điểm I của đoạn thẳng AB:
)
Tọa độ trọng tâm G của tam giác ABC: