LỚP 12 HÌNH HỌC
Chương 2: MẶT NÓN, MẶT TRỤ, MẶT CẦU
Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY I
SỰ TẠO THÀNH MẶT TRÒN XOAY
II MẶT NÓN TRÒN XOAY
Quan sát các hình ảnh sau Nếu dùng một mặt phẳng song song với
đáy cắt những đồ vật
này thì thiết diện tạo được là hình gì?
Giáo án Powerpoint Khái niệm về mặt tròn xoay Toán 12 Hình học
385
193 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Bộ bài giảng điện tử Toán 12 Hình học được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Bộ bài giảng powerpoint Toán 12 Hình học bao gồm đầy đủ các bài giảng trong cả năm học. Bộ bài giảng được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng phần học và bám sát chương trình Sách giáo khoa Toán 12 Hình học.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(385 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 10 đề thi Cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án150.000 ₫ 1.1 K 563 lượt tải
-
Bộ 10 đề thi Cuối kì 1 Toán 12 Kết nối tri thức có đáp án150.000 ₫ 1 K 491 lượt tải
-
Bộ 10 đề thi Cuối kì 1 Toán 12 Cánh diều có đáp án150.000 ₫ 503 252 lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án150.000 ₫ 9.7 K 4.8 K lượt tải
-
Bộ 15 đề thi HSG Toán 12 có lời giải200.000 ₫ 6.9 K 3.5 K lượt tải
-
Bài giảng Powerpoint Toán 12 Kết nối tri thức350.000 ₫ 2.4 K 1.2 K lượt tải
-
Bài giảng Powerpoint Toán 12 Chân trời sáng tạo350.000 ₫ 1.2 K 622 lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 12 Chân trời sáng tạo có đáp án150.000 ₫ 2.8 K 1.4 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 12
Xem thêm-
Bộ 3 đề thi giữa kì 1 Tin học 12 Kết nối tri thức có đáp án70.000 ₫ 5 K 2.5 K lượt tải
-
Trắc nghiệm Lịch sử 12 Đúng-Sai, Trả lời ngắn (form 2025300.000 ₫ 8.2 K 4.1 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Sinh học 12 Kết nối tri thức có đáp án70.000 ₫ 4.3 K 2.2 K lượt tải
-
Bộ 5 đề thi Cuối kì 1 Tiếng Anh 12 Friends global có đáp án90.000 ₫ 426 213 lượt tải
-
Bộ 3 đề thi giữa kì 1 Sinh học 12 Chân trời sáng tạo có đáp án70.000 ₫ 1.9 K 1 K lượt tải
-
Bộ 10 đề thi giữa kì 1 Ngữ văn 12 Kết nối tri thức có đáp án150.000 ₫ 5.7 K 2.8 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Vật lí 12 Chân trời sáng tạo có đáp án70.000 ₫ 1.7 K 830 lượt tải
-
Bộ 6 đề thi giữa kì 1 Lịch sử 12 Cánh diều có đáp án100.000 ₫ 5.6 K 2.8 K lượt tải
Tài liệu bộ mới nhất
HÌNH HỌC
Chương 2: MẶT NÓN, MẶT TRỤ, MẶT CẦU
LỚP
12
MẶT NÓN TRÒN XOAY
II
SỰ TẠO THÀNH MẶT TRÒN XOAY
I
Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY
Quan sát các hình ảnh sau
Nếu dùng một mặt
phẳng song song với
đáy cắt những đồ vật
này thì thiết diện tạo
được là hình gì?
Trong không gian, mặt phẳng chứa đường thẳng
và đường Khi quay quay quanh một
góc 360
0
thì:
Mỗi điểm vạch ra một đường tròn tâm
O và nằm trên mp vuông góc với
Đường sẽ tạo nên một hình được gọi là mặt
tròn xoay.
O
+ Đường : Đường sinh của mặt tròn xoay
+ Đường thẳng : Trục của mặt tròn xoay
SỰ TẠO THÀNH MẶT TRÒN XOAY
I
Bình gốm
Chi tiết máy
Viên đạn
Ấm trà Nón Lá
Ly nước
Đai ốc lục giác
Mũi khoan
ĐỒ VẬT NÀO SAU ĐÂY CÓ BỀ MẶT NGOÀI LÀ MẶT TRÒN XOAY?
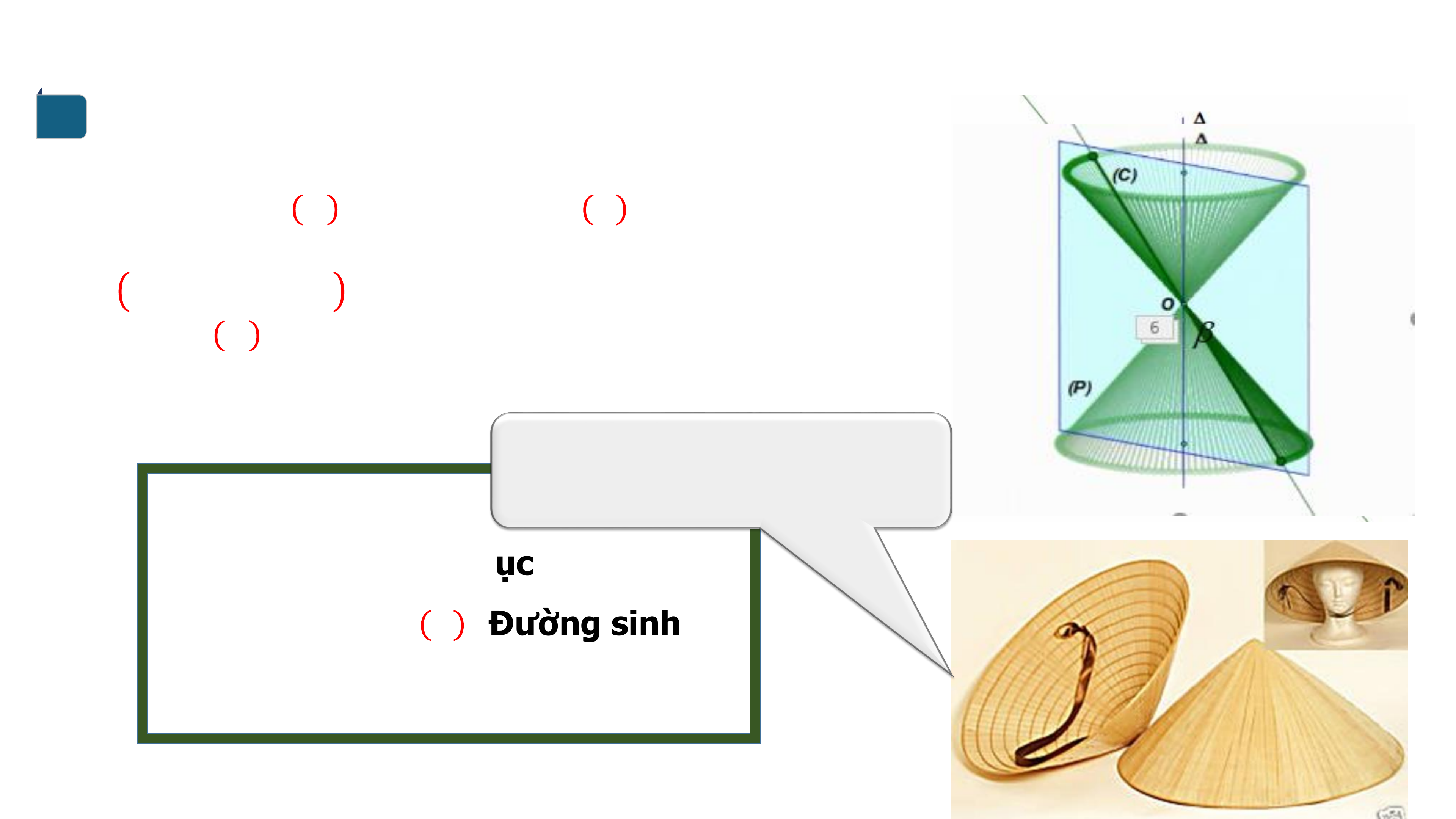
Trong mp có hai đường và đường thẳng
cắt nhau tại điểm và tạo thành góc nhọn
.
Quay xung quanh một góc
.
Đường thẳng sinh ra một hình gọi là mặt
nón tròn xoay.
+ Đỉnh .
+ Đường thẳng : Trục
+ Đường thẳng : Đường sinh
+ Góc ở đỉnh :
1. ĐỊNH NGHĨA
MẶT NÓN TRÒN XOAY
II
Đây chỉ là một phần của
mặt nón tròn xoay
MẶT NÓN TRÒN XOAY
II
2. HÌNH NÓN TRÒN XOAY VÀ KHỐI NÓN TRÒN XOAY
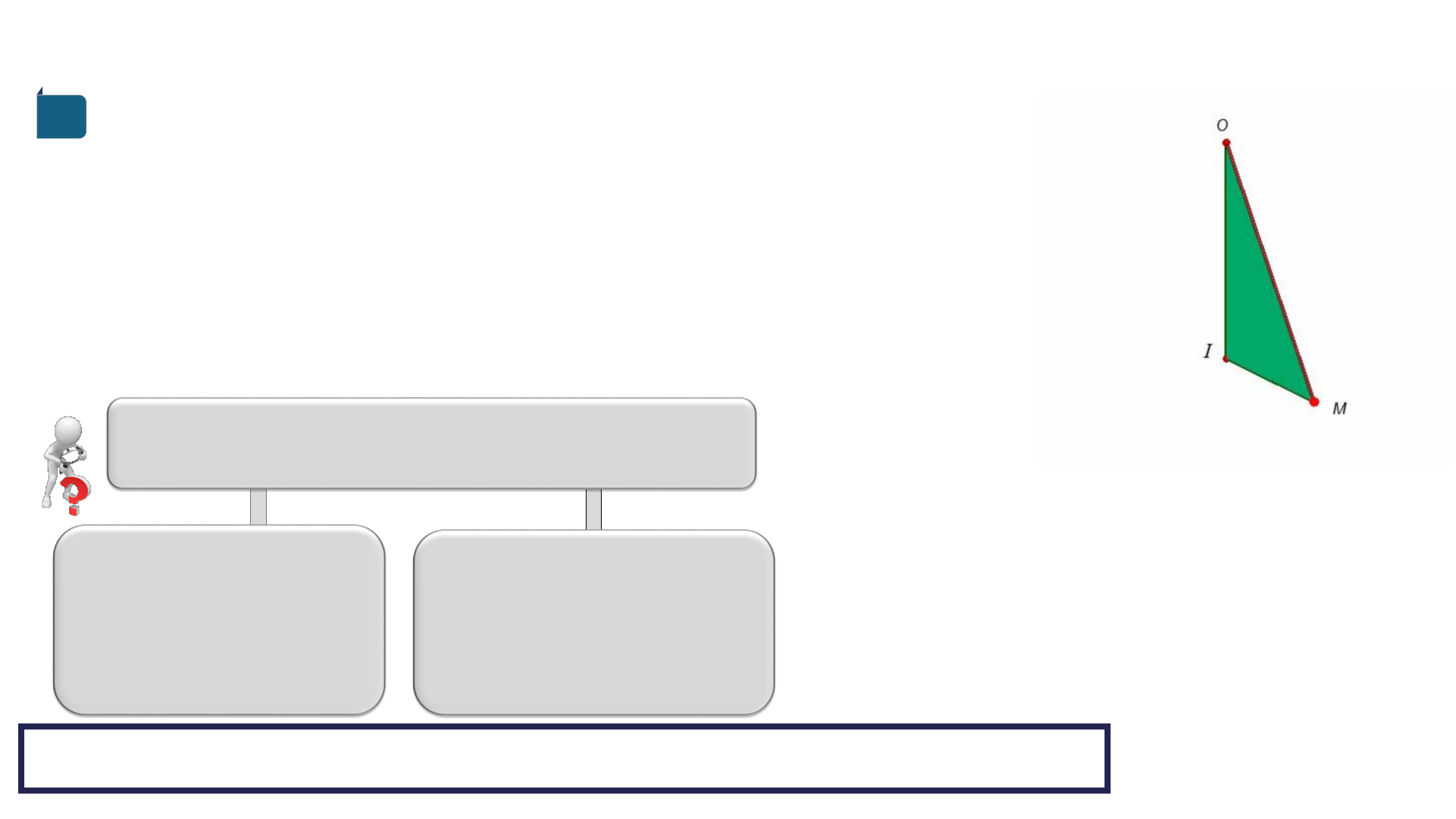
Cho vuông tại Khi quay xung quanh cạnh góc
vuông thì đường gấp khúc tạo thành một hình gọi
là hình nón tròn xoay.
a) Hình nón tròn xoay:
Khi quay quanh , cạnh và
tạo thành hình gì?
tạo thành hình
tròn tâm , bán
kính – gọi là
mặt đáy.
tạo thành một
phần nón tròn xoay
– gọi là mặt xung
quanh.
Vậy hình nón hợp của hai phần: Mặt đáy và mặt xung quanh
MẶT NÓN TRÒN XOAY
II
2. HÌNH NÓN TRÒN XOAY VÀ KHỐI NÓN TRÒN XOAY
a) Hình nón tròn xoay:
– Mặt đáy: Là hình tròn
– Phần mặt xung quanh: Là phần
mặt tròn xoay sinh bởi quay xung
quanh .
* Gồm hai phần :
* Đặc điểm: – Đỉnh:
O
I
M
Đỉnh O
Đường
cao OI
Đường
Sinh OM
– Đường sinh:
– Đường cao:
MẶT NÓN TRÒN XOAY
II
2. HÌNH NÓN TRÒN XOAY VÀ KHỐI NÓN TRÒN XOAY
a) Hình nón tròn xoay:
Phần không gian được giới hạn bởi một hình
nón tròn xoay kể cả hình nón đó được gọi là
khối nón tròn xoay.
– Điểm ngoài: điểm không thuộc khối nón.
– Điểm trong: điểm thuộc khối nón nhưng
không thuộc hình nón.
là trung điểm của
thì thuộc khối nón
hay hình nón ?
O
I
M
H
là trung điểm của
thì thuộc khối
nón hay hình nón ?
K
b) Khối nón tròn xoay:
MẶT NÓN TRÒN XOAY
II
3. DIỆN TÍCH XUNG QUANH CỦA HÌNH NÓN TRÒN XOAY
Một hình chóp được gọi là nội tiếp một hình nón
nếu
đáy của hình chóp là đa giác nội tiếp đường
tròn đáy của hình nón
và đỉnh của hình chóp là đỉnh của hình nón
Khi đó ta nói hình nón ngoại tiếp hình chóp
a) Hình chóp nội tiếp hình nón tròn xoay
Diện tích xung quanh của hình nón
tròn xoay
là giới hạn của diện tích xung quanh
của hình chóp đều nội tiếp hình nón đó khi số
cạnh đáy tăng lên vô hạn.
* Định nghĩa:
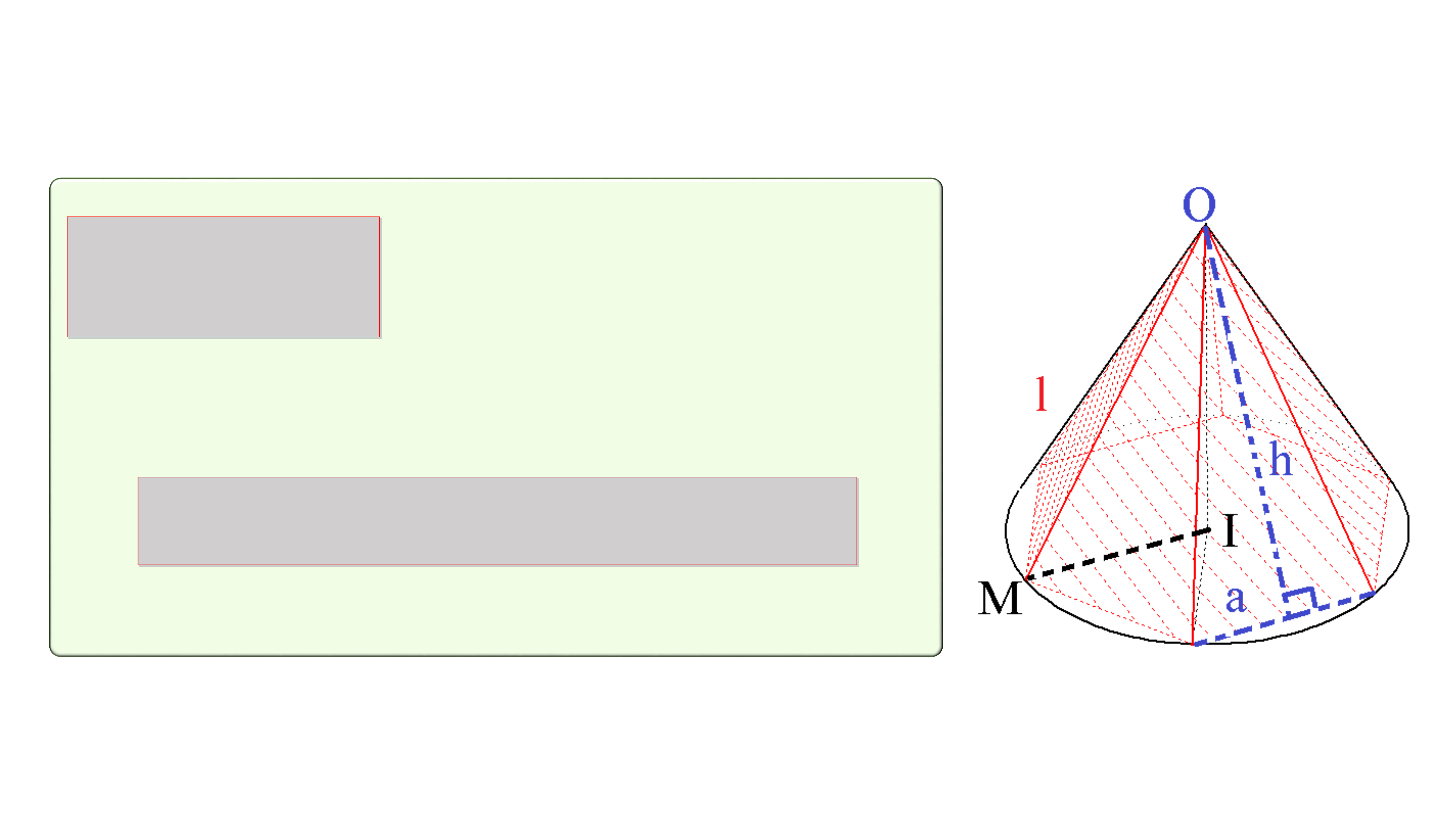
b) Công thức tính diện tích xung quanh của hình nón tròn xoay:
: bán kính đáy
: độ dài đường sinh
Ghi nhớ: Tổng của diện tích xung quanh và
diện tích đáy gọi là diện tích toàn phần
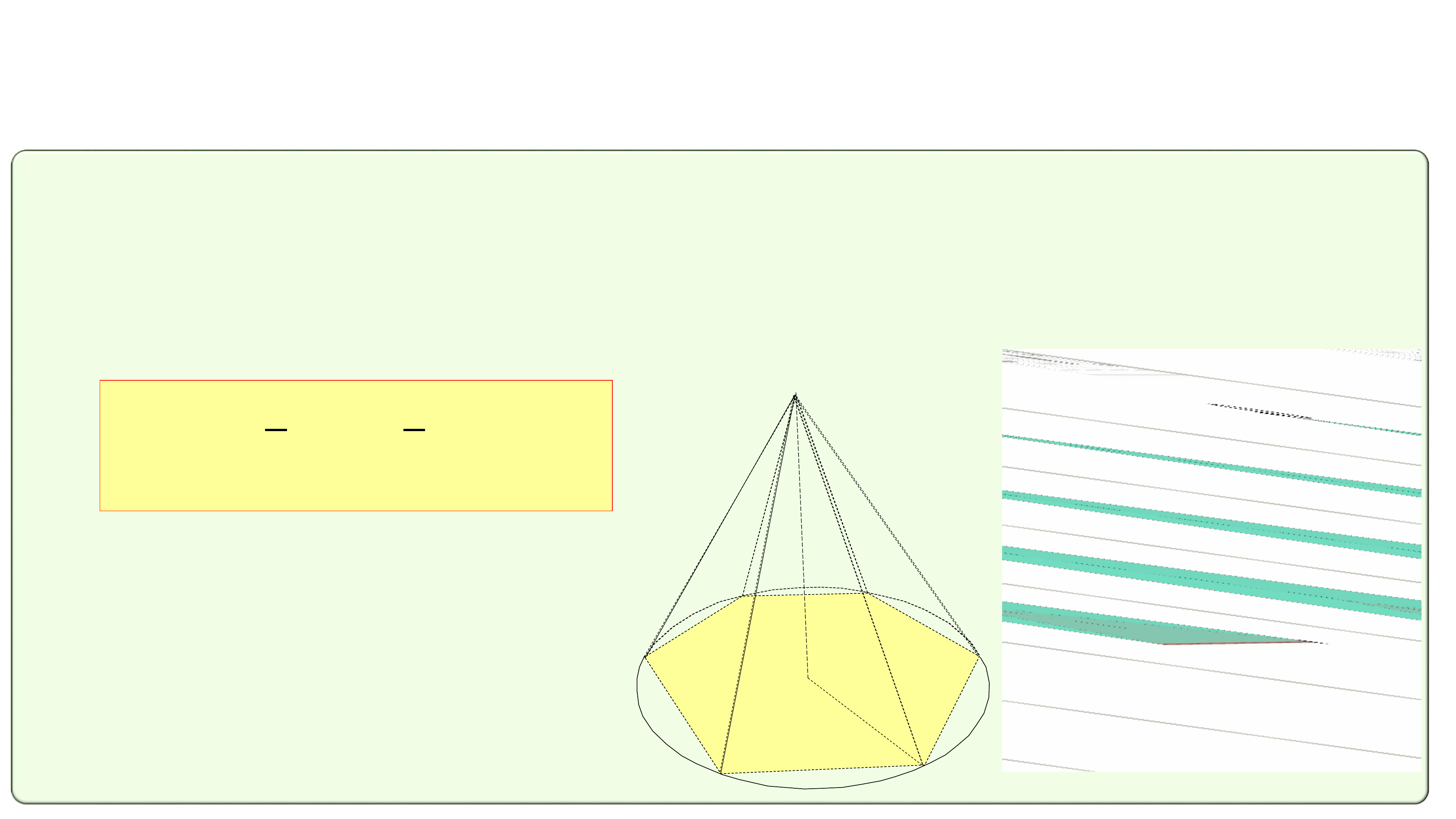
Thể tích khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội
tiếp khối nón đó khi số cạnh đáy tăng lên vô hạn
b) Công thức tính thể tích khối nón tròn xoay:
r
: bán kính
h
: chiều cao
4. THỂ TÍCH KHỐI NÓN TRÒN XOAY
a) Định nghĩa:
O
r
l
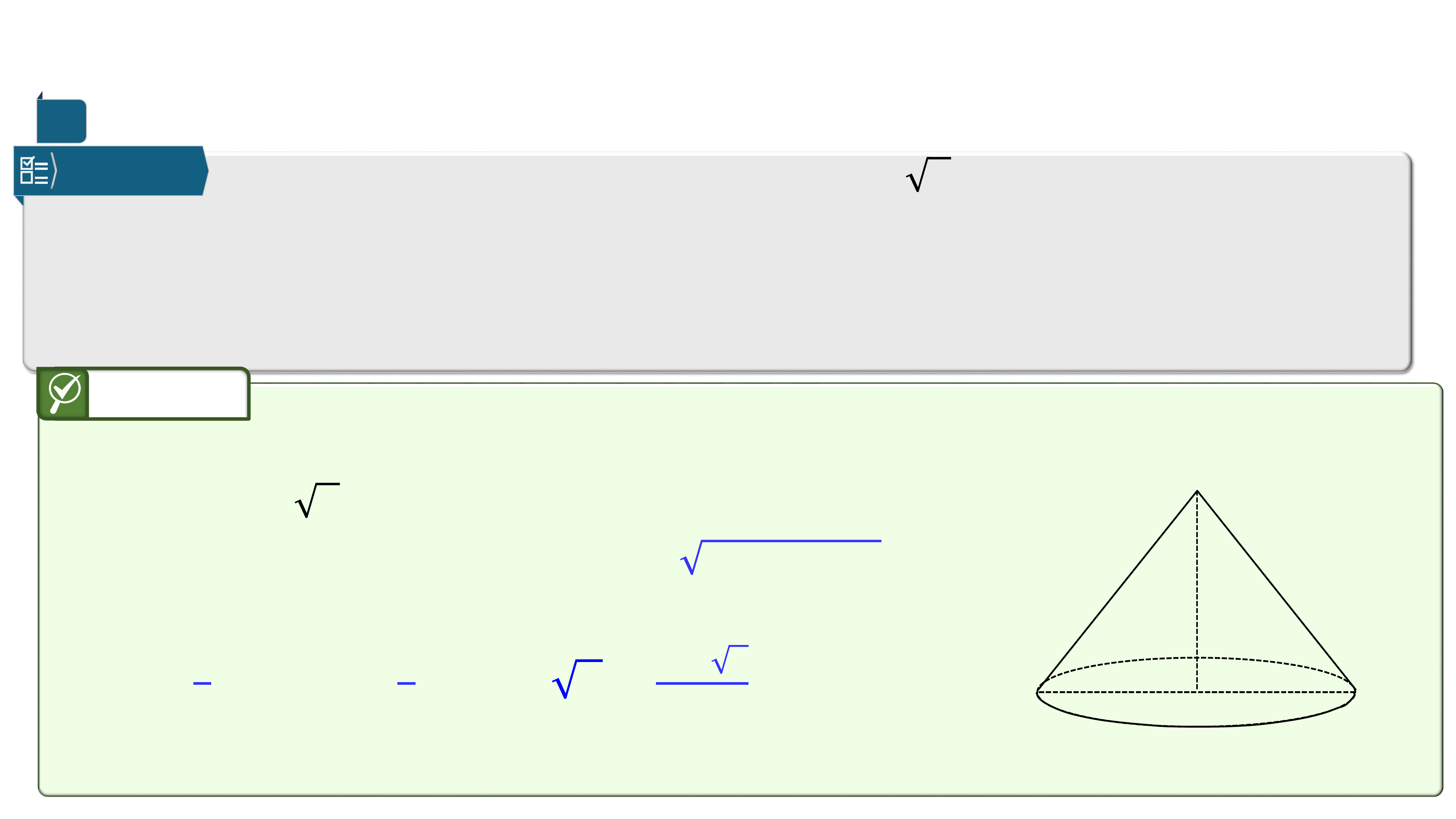
Ví dụ 1
Cho tam giác vuông tại và
Khi quay tam giác quanh trục ta được một hình nón tròn xoay.
a) Tính thể tích khối nón .
b) Tính diện tích xung quanh của hình nón.
Bài giải
a) Hình nón nhận được có đỉnh là
tâm đường tròn đáy là chiều cao hình nón là
độ dài đường sinh là
Suy ra bán kính đáy là
Thể tích khối nón
b)
.
MẶT NÓN TRÒN XOAY
II
A
C
B
h
l
r
Thể tích khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội
tiếp khối nón đó khi số cạnh đáy tăng lên vô hạn
b) Công thức tính thể tích khối nón tròn xoay:
r
: bán kính
h
: chiều cao
4. THỂ TÍCH KHỐI NÓN TRÒN XOAY
a) Định nghĩa:
O
r
l
Ví dụ 2:
Cắt hình nón đỉnh bới một mặt phẳng đi qua trục của hình nón
ta được một tam giác vuông cân có cạnh huyền bằng , là dây cung
của đường tròn đáy hình nón sao cho mặt phẳng tạo với mặt phẳng
chứa đáy hình nón một góc . Tính theo diện tích của tam giác .
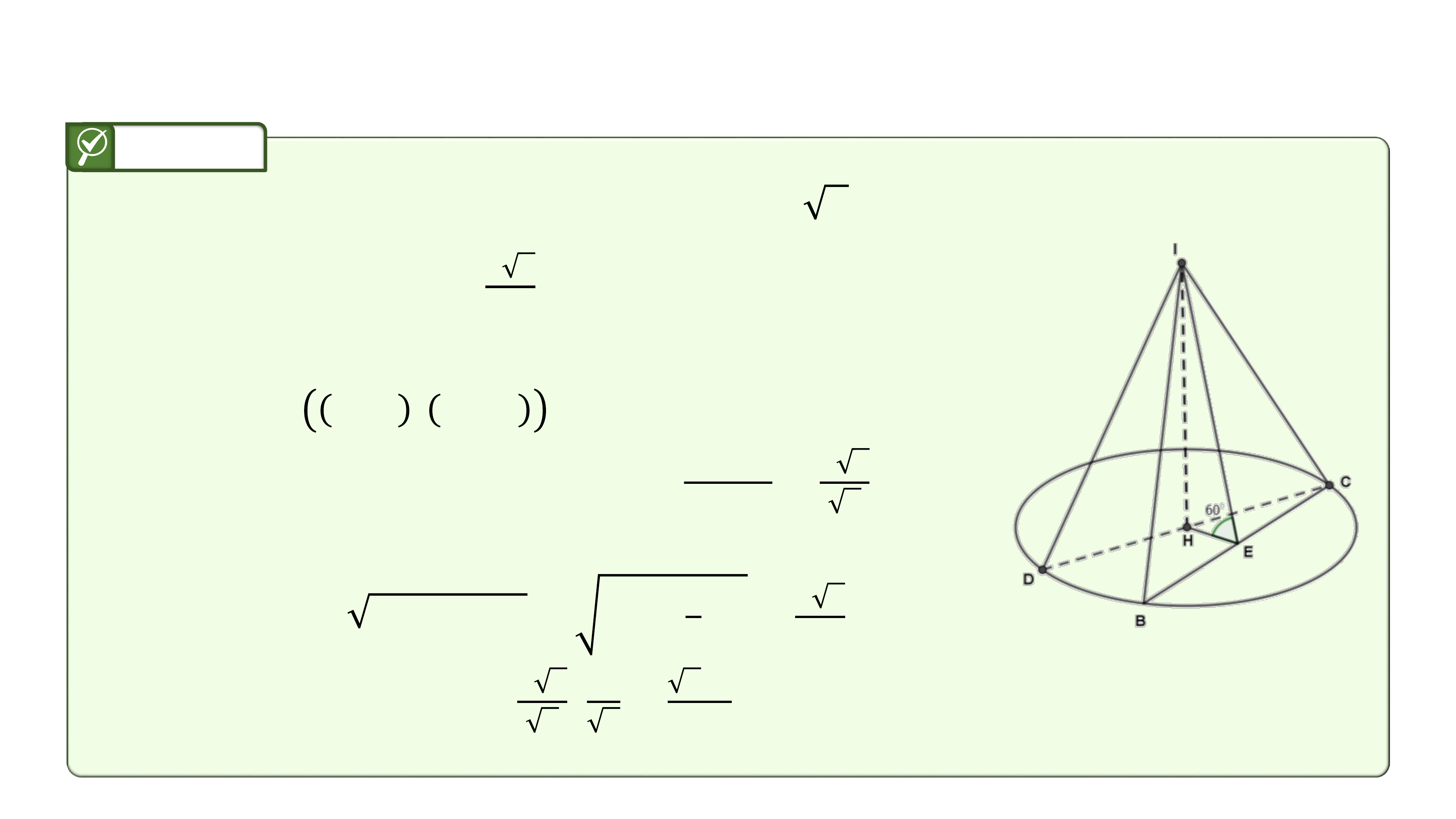
Bài giải
Tam giác vuông cân có
và
Gọi là trung điểm cạnh ,
Trong tam giác có
Tam giác có
.
.
Bài giải
Câu 1.
Cho đường thẳng cắt và không vuông góc với quay quanh thì ta
được
A. Hình nón tròn xoay.
B. Mặt nón tròn xoay.
C. Khối nón tròn xoay.
D. Mặt trụ tròn xoay.
Theo định nghĩa.
B.
Chọn B.
Bài giải
Câu 2.
Cho tam giác vuông tại . Khi quay tam giác (kể cả các điểm
trong) quanh cạnh ta được
A. Khối nón.
B. Mặt nón.
C. Khối trụ.
D. Khối cầu.
Theo định nghĩa.
A.
Chọn A.
A
B
C
Bài giải
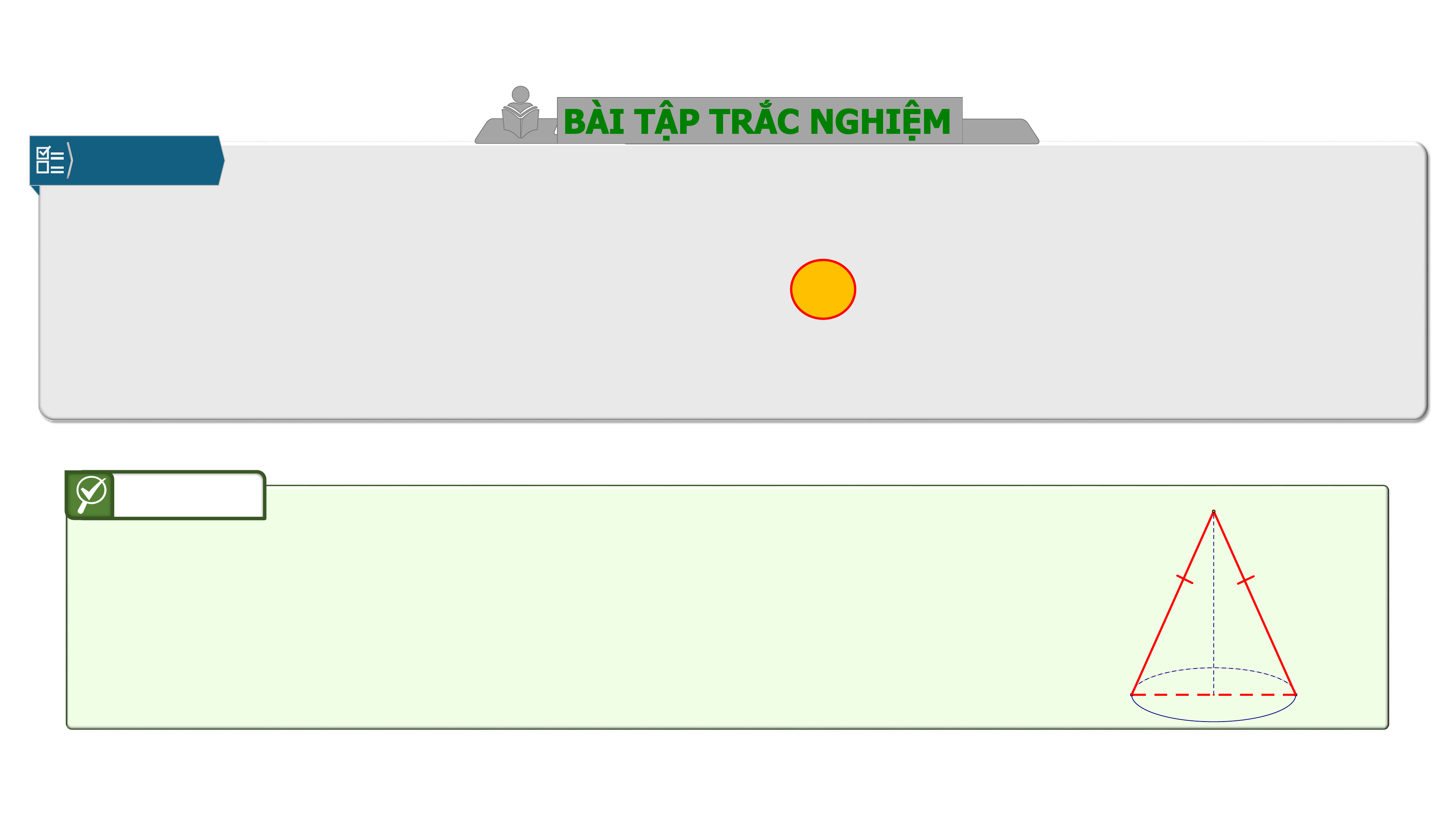
Câu 3.
Mặt phẳng chứa trục của một hình nón cắt hình nón theo thiết diện là:
A. Một hình chữ nhật.
B. Một tam giác cân.
C. Một đường elip.
D. Một đường tròn.
Mặt phẳng chứa trục của một hình nón cắt
hình nón theo thiết diện là một tam giác
cân.
B.
A
B
S
Chọn B.
Bài giải
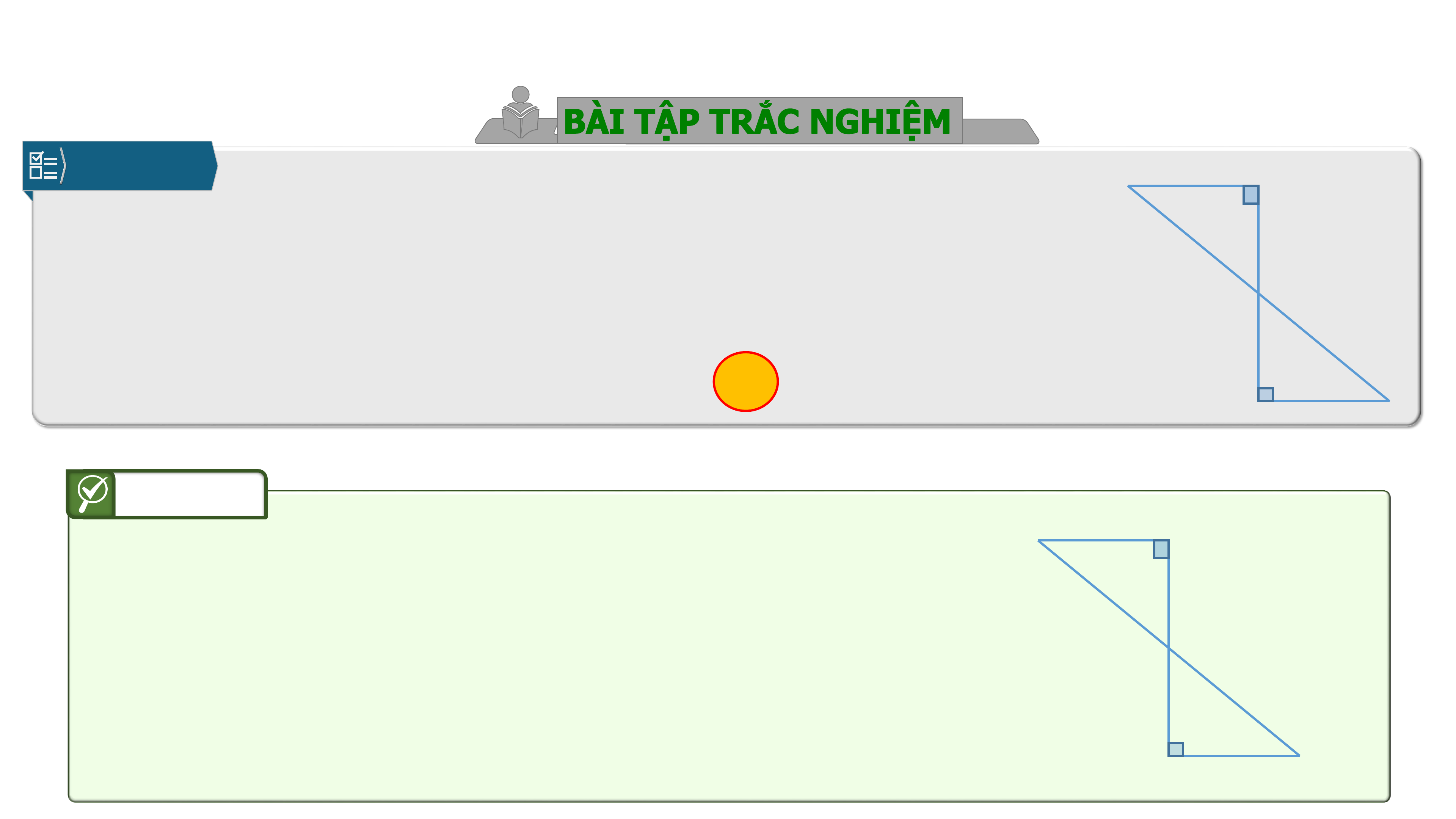
Câu 4.
Hình (như hình bên) khi quay quanh thì tạo ra:
A. Một hình trụ.
B. Một hình nón.
C. Một hình nón cụt.
D. Hai hình nón.
Gọi là giao điểm của AD và BC.
Khi quay hình quanh trục
thì tạo thành hai hình nón
chung đỉnh .
D.
Chọn D.
A
B
C D
A
B
C D
Bài giải
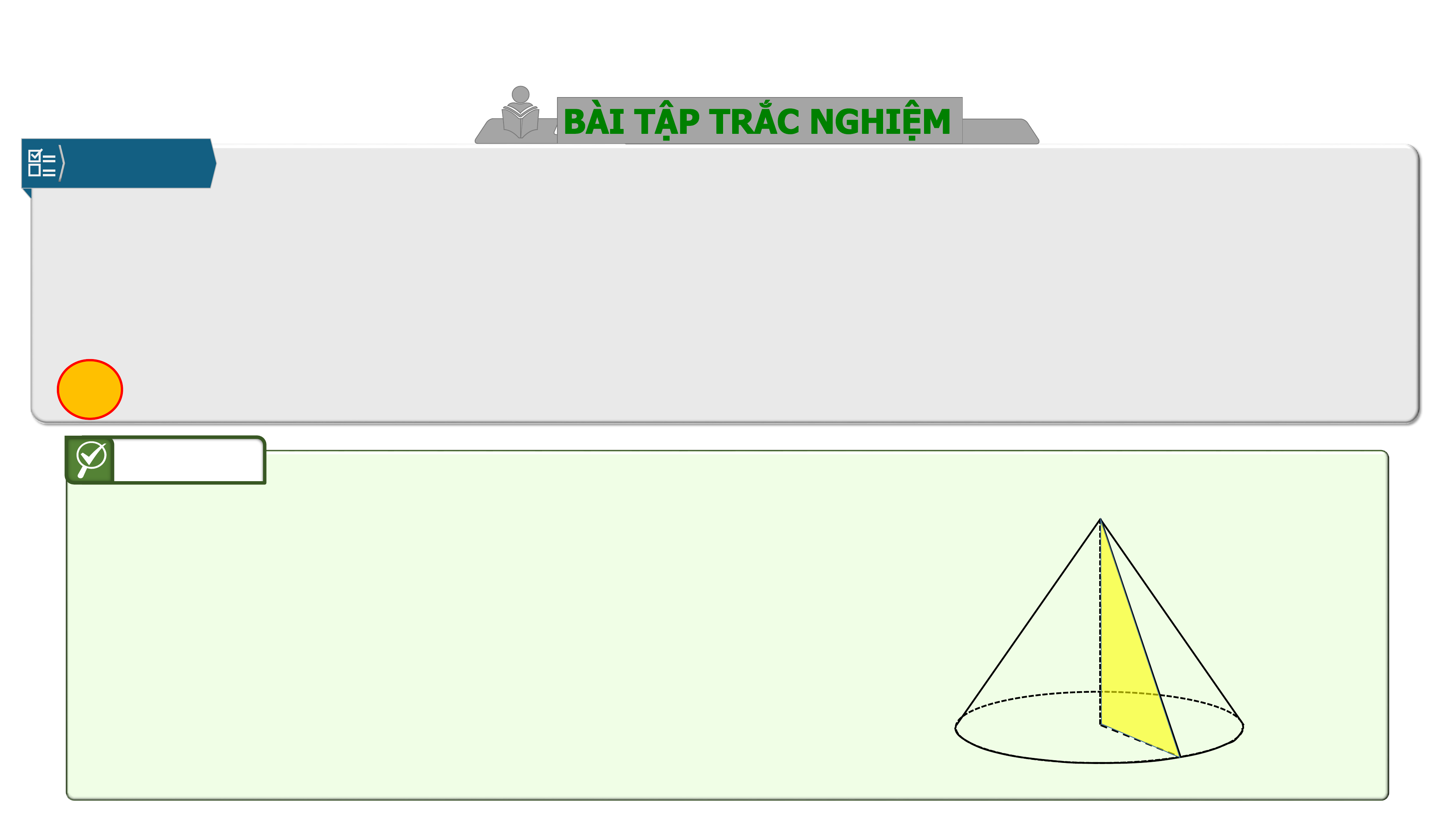
Câu 5.
Gọi , , lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của
hình nón. Đẳng thức luôn đúng là
A. .
B. .
C.
.
D.
.
Xét tam giác vuông tại O.
Ta có:
.
Vậy
.
C.
Chọn C.
O
A
S
Bài giải
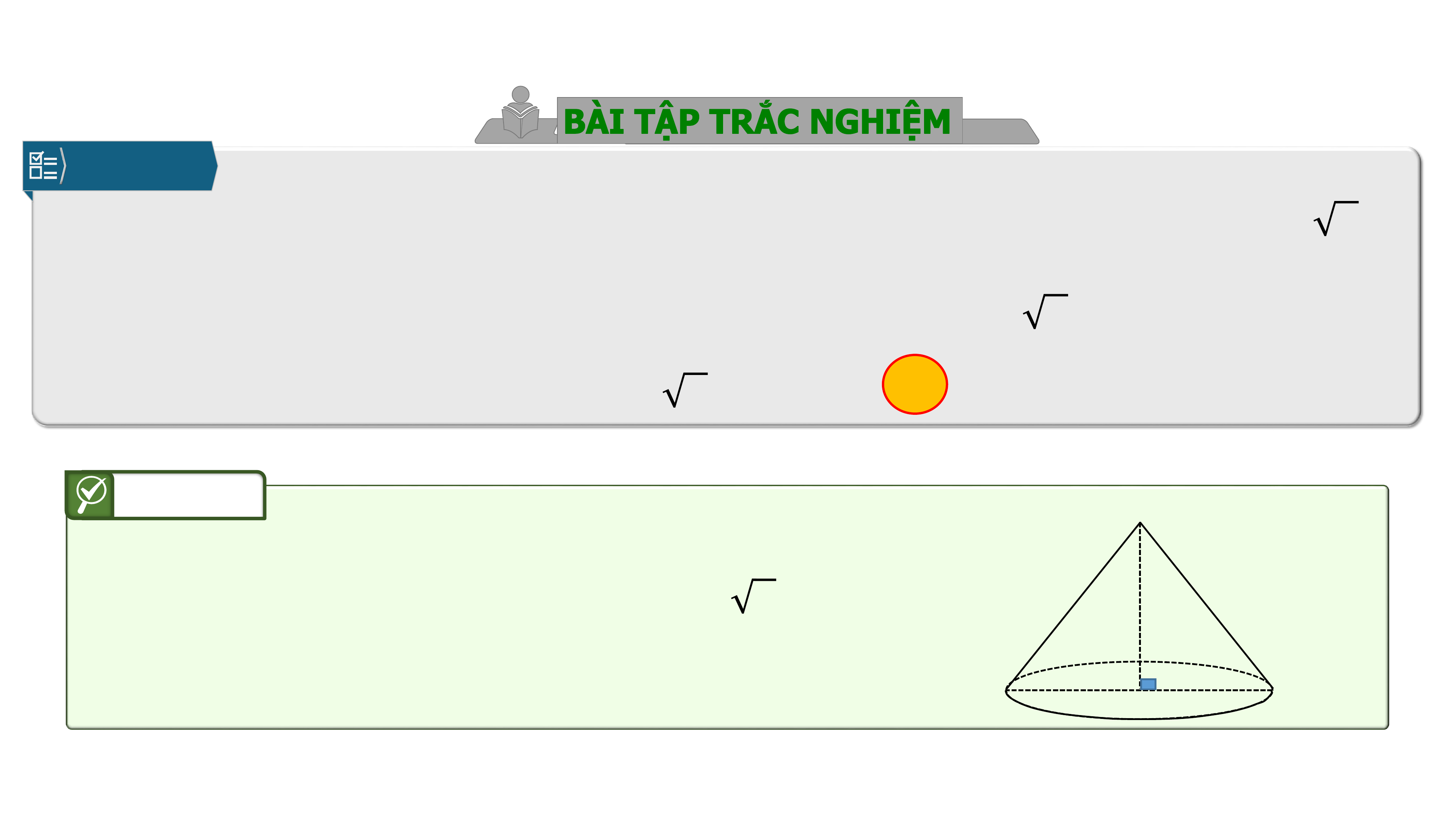
Câu 6.
Trong không gian cho tam giác vuông tại , và .
Tính độ dài đường sinh của hình nón có được khi quay tam giác
xung quanh trục .
A. .
B. .
C. .
D. .
Xét tam giác vuông tại .
Ta có:
=
=4a
.
Vậy .
D.
Chọn D.
A
C
B
Bài giải
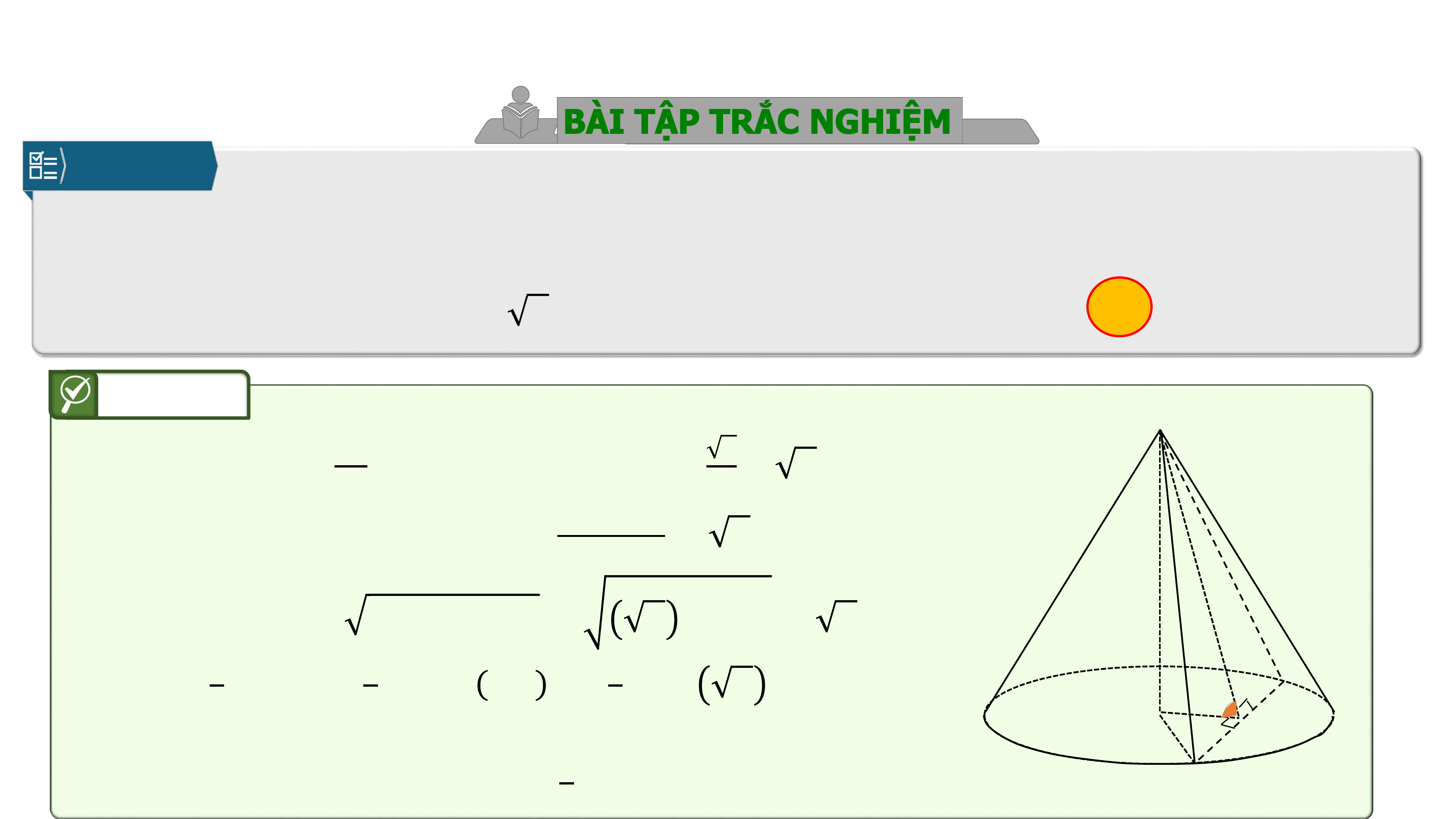
Câu 7.
Cho hình nón có thiết diện qua đỉnh tạo với đáy góc
là tam giác đều
cạnh bằng . Thể tích của khối nón đó là
A.
.
B.
.
C.
. D.
.
Gọi thiết diện qua đỉnh là , tâm đường tròn đáy là .
Góc giữa và đáy:
.
Suy ra
Giả thiết cho đều cạnh
S
O
A
B
H
Bài giải
Câu 7.
Cho hình nón có thiết diện qua đỉnh tạo với đáy góc
là tam giác đều
cạnh bằng . Thể tích của khối nón đó là
A.
.
B.
.
C.
. D.
.
;
Chọn D
Ghi nhớ công thức:
D.
S
O
A
B
H
Bài giải
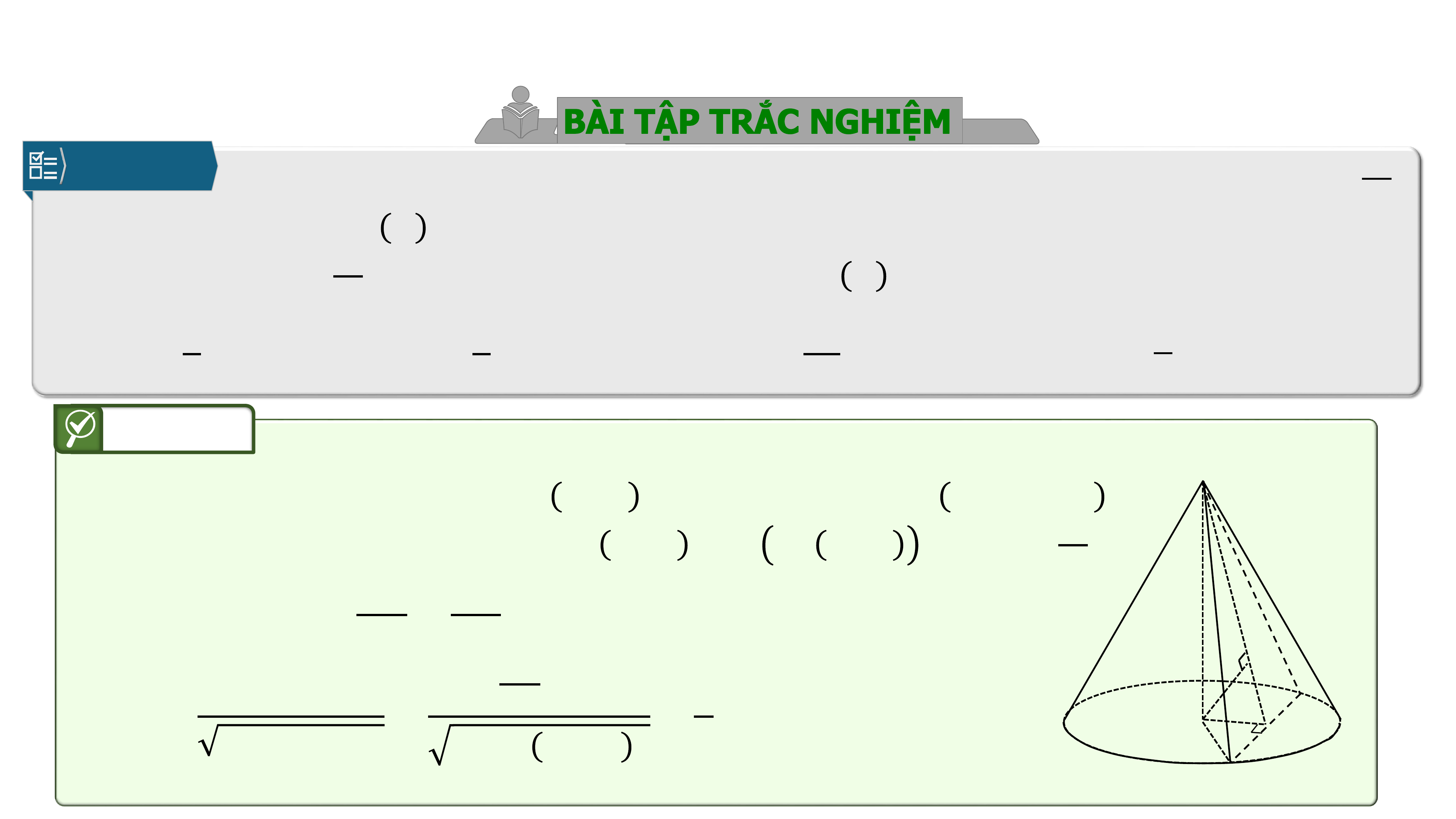
Câu 8.
Cho khối nón tròn xoay có đường cao và bán kính đáy
.
Một mặt phẳng đi qua đỉnh của khối nón và có khoảng cách đến tâm
của đáy bằng
. Diện tích thiết diện tạo bởi và hình nón là
A.
. B.
. C.
.
D.
.
Gọi thiết diện qua đỉnh là .
* Khoảng cách từ đến mặt . Từ kẻ ,
nối , từ kẻ
S
O
A
B
H
K
Bài giải
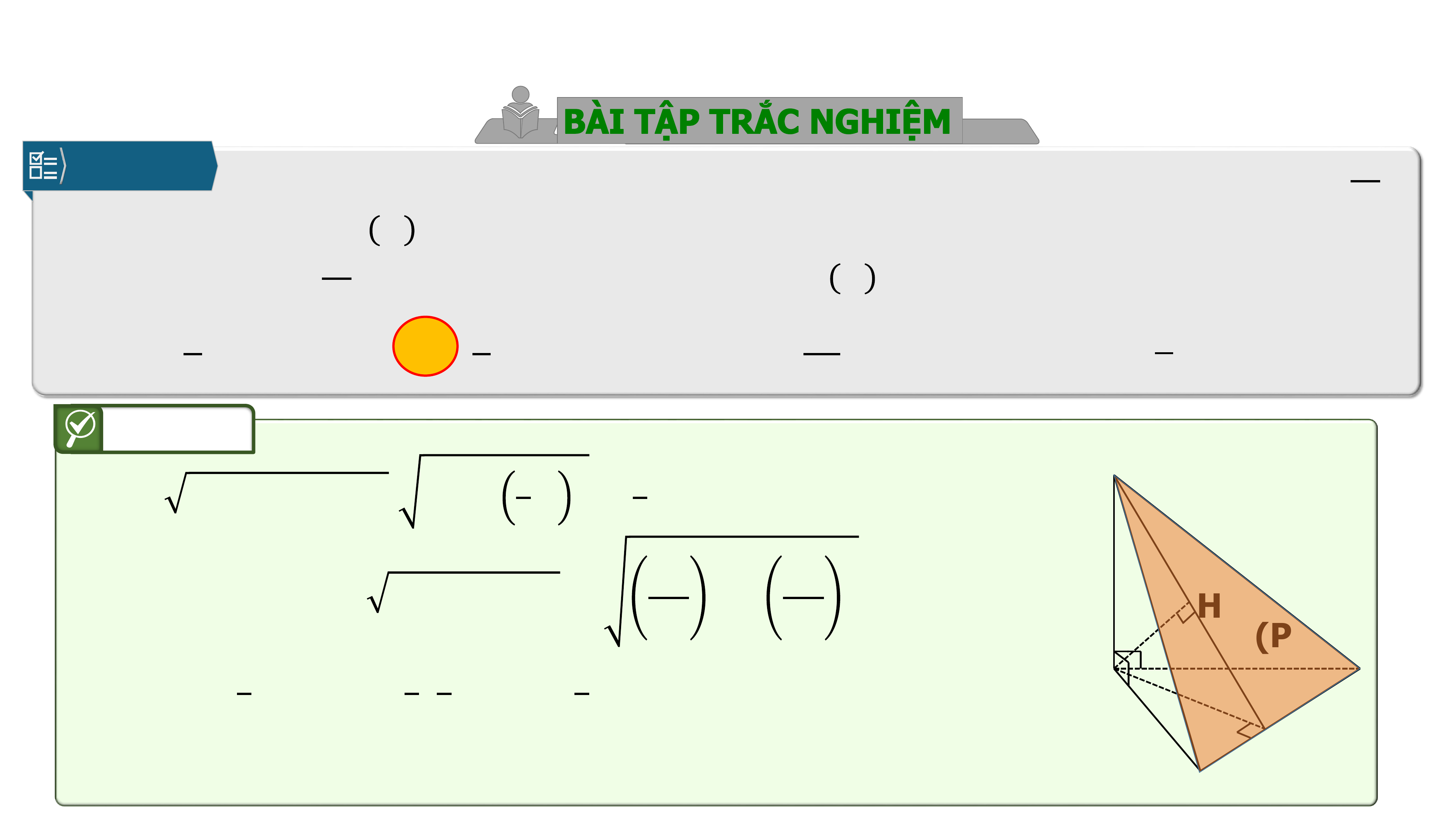
Câu 8.
Cho khối nón tròn xoay có đường cao và bán kính đáy
.
Một mặt phẳng đi qua đỉnh của khối nón và có khoảng cách đến tâm
của đáy bằng
. Diện tích thiết diện tạo bởi và hình nón là
A.
. B.
. C.
.
D.
.
Vậy
Chọn B
Chú ý bài toán khoảng cách cơ bản
B.
S
A
H
K
(P)
B
O
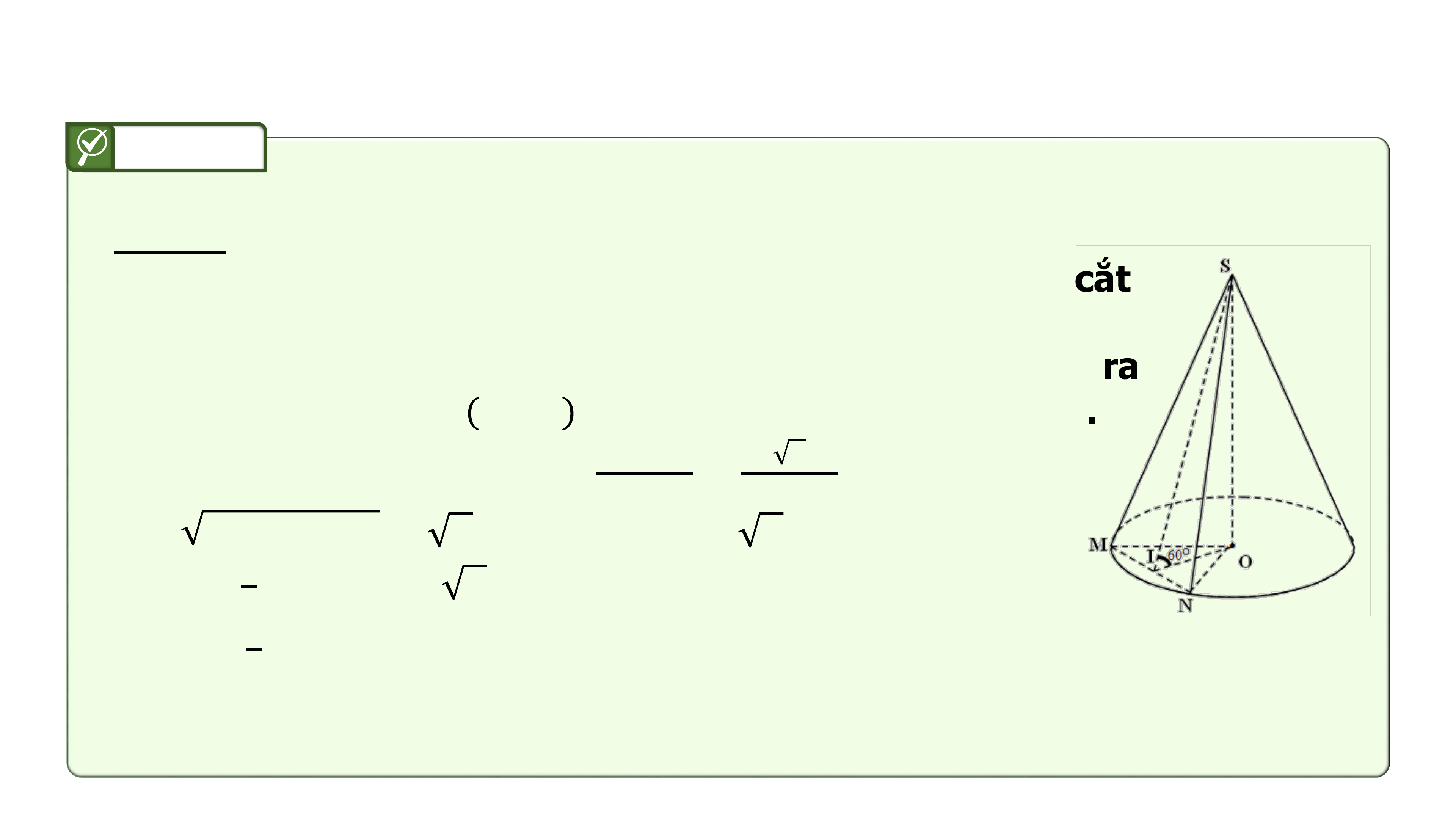
Câu 9:
Một khối nón có bán kính đáy bằng cm, chiều cao bằng cm.
Một mặt phẳng đi qua đỉnh và tạo với đáy một góc
chia khối nón làm
phần. Tính thể tích phần nhỏ hơn (Tính gần đúng đến hàng phần trăm).
D.cm
.
A.cm
.
B.cm
. C.cm
.
A.
Bài giải
Cách 1:
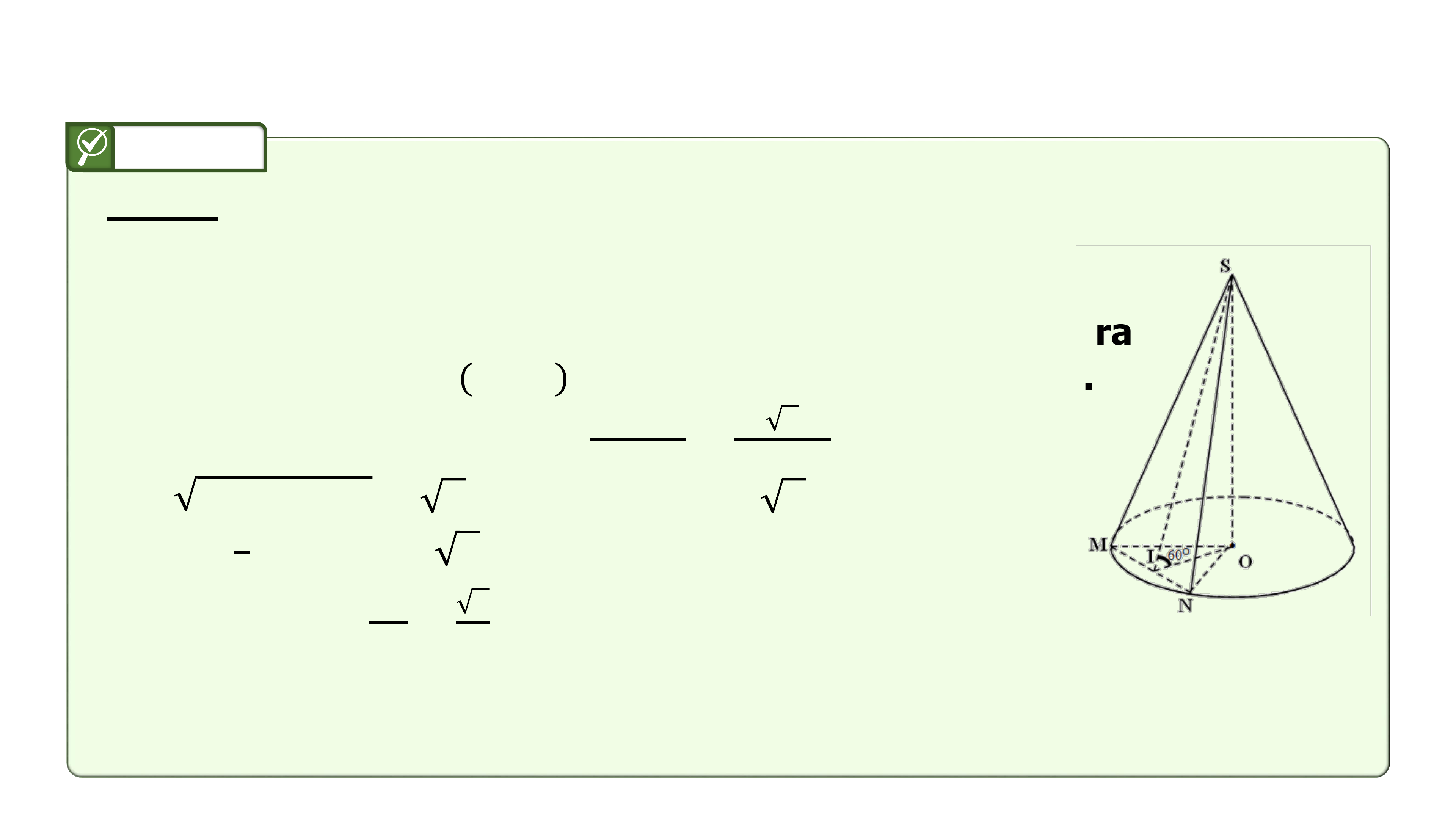
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc cắt
khối nón theo thiết diện là tam giác như hình vẽ.
Gọi là trung điểm . Khi đó và , suy ra
góc giữa mặt phẳng và mặt đáy là góc
.
Xét tam giác ta có:
.
, .
.
.
Bài giải
.
.
Suy ra
,
.
Gọi là thể tích cần tính.
Ta có
cm
.
Bài giải
Cách 2:
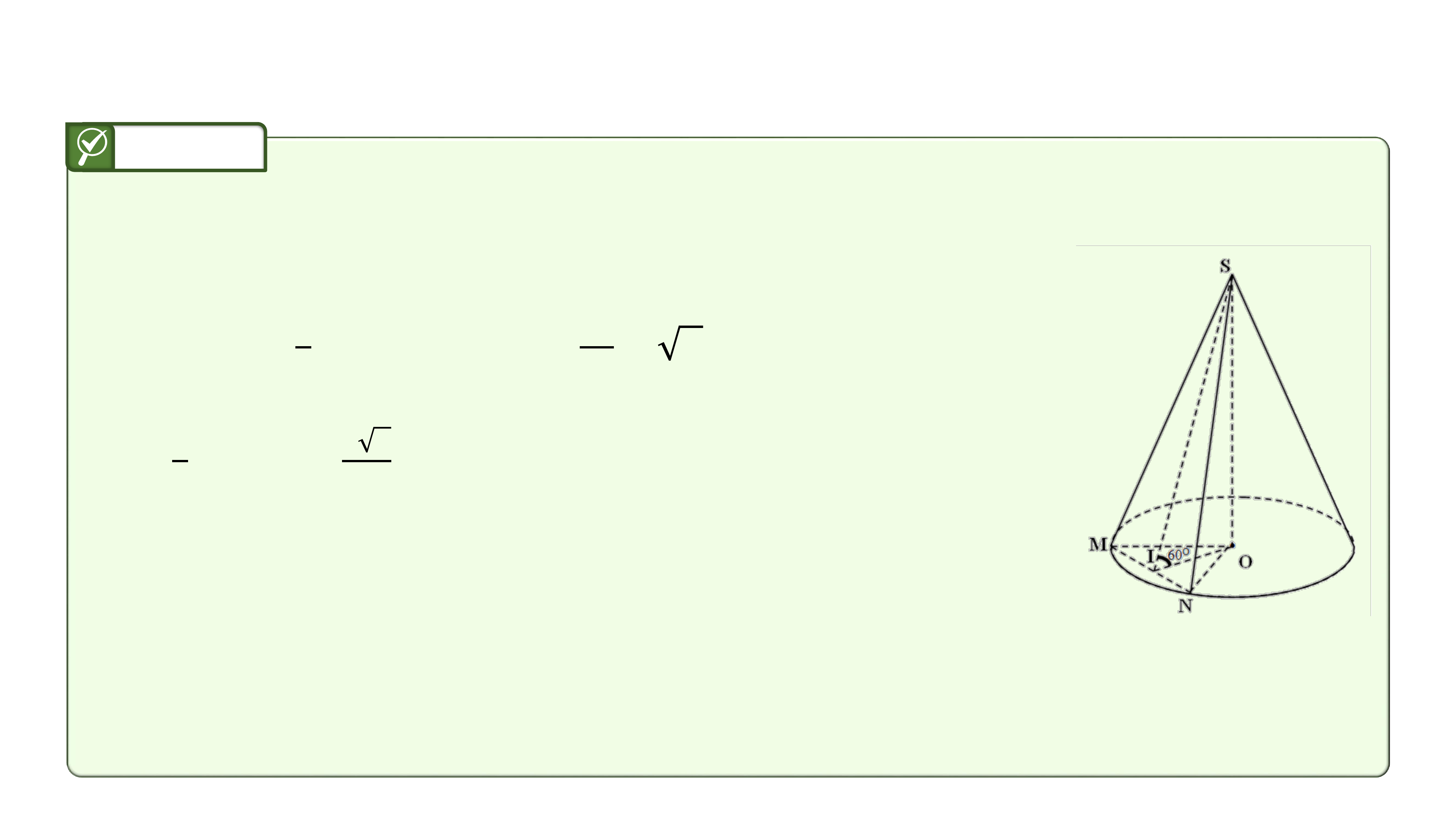
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc cắt
khối nón theo thiết diện là tam giác như hình vẽ.
Gọi là trung điểm . Khi đó và , suy ra
góc giữa mặt phẳng và mặt đáy là góc
.
Xét tam giác ta có:
.
.
.
Ta có
suy ra
,
.
Bài giải
Gọi
là diện tích hình viên phân tạo bởi dây và cung
nhỏ .
Ta có
Thể tích phần nhỏ cần tính là:
cm
.
Câu 10:
Một cái phễu có dạng hình nón. Người ta đổ một lượng
nước vào phễu sao cho chiều cao của lượng nước trong
phễu bằng một phần ba chiều cao của phễu. Hỏi nếu
bịt miệng phễu rồi lật ngược phễu lên thì chiều cao của
nước bằng bao nhiêu? Biết chiều cao của phễu là
D. .
A. .
B. .
C. .
D.
Bài giải
Gọi cm là chiều cao của phễu và là thể tích
của phễu hình nón.
Ký hiệu
cm là chiều cao và
là thể tích
của lượng nước trong phễu.
Gọi
,
là chiều cao và thể tích của phần không
gian (hình nón) trống trong phễu khi lật ngược phễu
lại.
Ta có
,
và
.
h
1
h
h
2
h
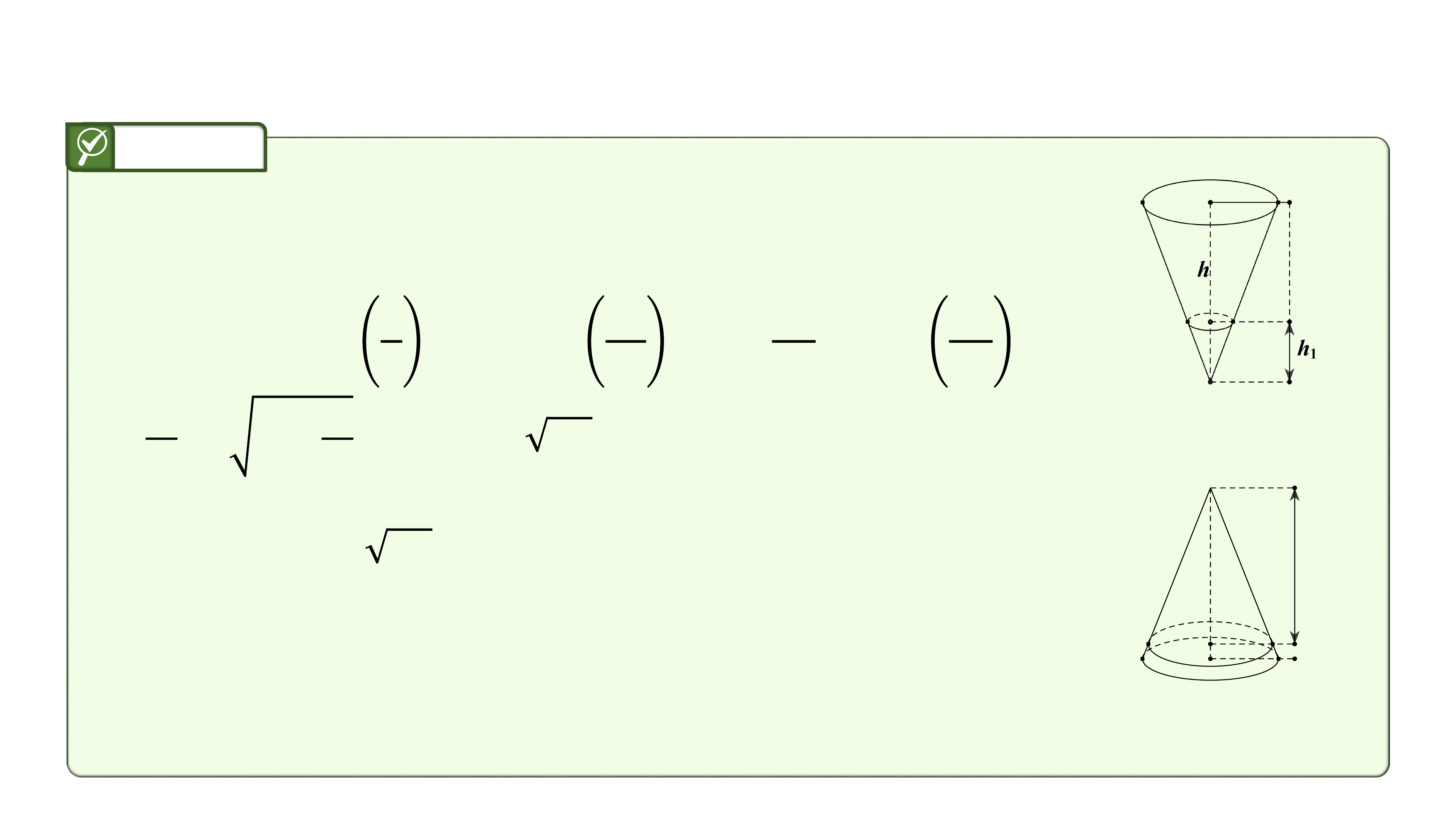
Bài giải
Khi đó,
.
Vậy chiều cao của nước khi lật ngược phễu lại là
cm.
h
2
h
Nhắn tin Zalo