LỚP HÌNH HỌC12
Chương 2: MẶT NÓN-MẶT TRỤ-MẶT CẦU Bài 2. MẶT CẦU I
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN II
GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG
III GIAO CỦA MẶT CẦU VỚI ĐƯỜNG THẲNG.
TIẾP TUYẾN CỦA MẶT CẦU IV
CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU
VÀ THỂ TÍCH KHỐI CẦU
Giới thiệu một số hình ảnh I
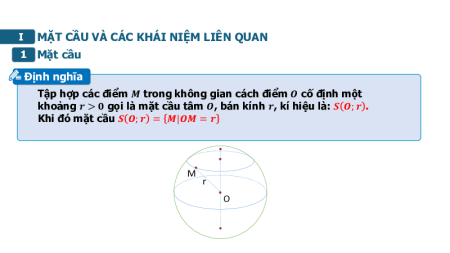
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN 1 Mặt cầu Định nghĩa
Tập hợp các điểm ? trong không gian cách điểm ? cố định một
khoảng ? > ? gọi là mặt cầu tâm ?, bán kính ?, kí hiệu là: ? ?; ? .
Khi đó mặt cầu ? ?; ? = ?|?? = ? M r O
I MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN 1 Mặt cầu C D Chú ý Nếu 2 điểm O
?, ? nằm trên mặt cầu ? ?, ? thì
đoạn thẳng ?? được gọi là dây cung của mặt cầu ? . B
Dây cung ?? đi qua tâm ? được gọi là một
đường kính của mặt cầu ? . O A
Giáo án Powerpoint Mặt cầu Toán 12 Hình học
355
178 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Bộ bài giảng điện tử Toán 12 Hình học được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Bộ bài giảng powerpoint Toán 12 Hình học bao gồm đầy đủ các bài giảng trong cả năm học. Bộ bài giảng được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng phần học và bám sát chương trình Sách giáo khoa Toán 12 Hình học.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(355 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 15 đề thi giữa kì 1 Toán lớp 5 Kết nối tri thức có đáp án150.000 ₫ - 180.000 ₫ 23.5 K 11.7 K lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án150.000 ₫ 11.7 K 5.9 K lượt tải
-
Bộ 7 đề thi giữa kì 1 Toán lớp 4 Kết nối tri thức có đáp án110.000 ₫ 79.3 K 39.6 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Toán lớp 5 Chân trời sáng tạo có đáp án150.000 ₫ - 180.000 ₫ 11 K 5.5 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Toán 6 Kết nối tri thức có đáp án150.000 ₫ 20.3 K 10.1 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Toán lớp 5 Cánh diều có đáp án150.000 ₫ - 180.000 ₫ 7.3 K 3.7 K lượt tải
-
Bộ 26 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án150.000 ₫ - 200.000 ₫ 36.2 K 18.1 K lượt tải
-
Bài tập cuối tuần Toán lớp 5 Kết nối tri thức (Cả năm250.000 ₫ 38.5 K 19.2 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 12
Xem thêm-
Bộ 3 đề thi giữa kì 1 Tin học 12 Kết nối tri thức có đáp án70.000 ₫ 2.5 K 1.3 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Vật lí 12 Kết nối tri thức có đáp án70.000 ₫ 3.3 K 1.7 K lượt tải
-
Bộ 6 đề thi giữa kì 1 Lịch sử 12 Cánh diều có đáp án100.000 ₫ 2.8 K 1.4 K lượt tải
-
Bộ 5 đề thi giữa kì 1 Lịch sử 12 Kết nối tri thức có đáp án90.000 ₫ 2.8 K 1.4 K lượt tải
-
Bộ 5 đề thi giữa kì 1 Tiếng Anh 12 Global success có đáp án90.000 ₫ 2.2 K 1.1 K lượt tải
-
Trắc nghiệm Lịch sử 12 Đúng-Sai, Trả lời ngắn (form 2025300.000 ₫ 5.5 K 2.8 K lượt tải
-
Bộ 5 đề thi giữa kì 1 Tiếng Anh 12 Friends global có đáp án90.000 ₫ 2.2 K 1.1 K lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án150.000 ₫ 7.2 K 3.6 K lượt tải
Tài liệu bộ mới nhất
HÌNH HỌC
Chương 2: MẶT NÓN-MẶT TRỤ-MẶT CẦU
Bài 2. MẶT CẦU
LỚP
12
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN
I
GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG
II
CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU
VÀ THỂ TÍCH KHỐI CẦU
IV
GIAO CỦA MẶT CẦU VỚI ĐƯỜNG THẲNG.
TIẾP TUYẾN CỦA MẶT CẦU
III
Giới thiệu một số hình ảnh
I
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN
Mặt cầu
1
Định nghĩa
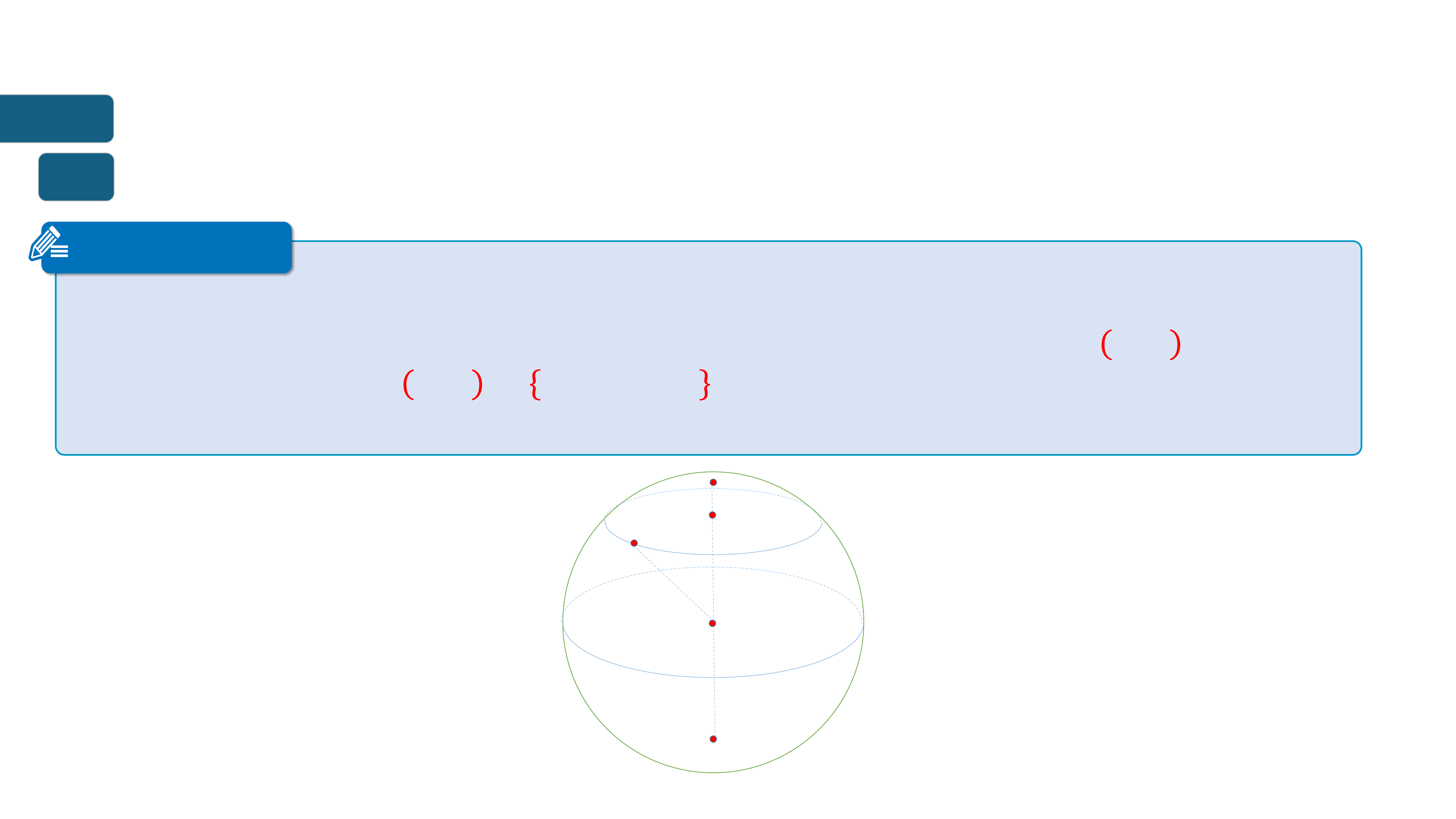
Tp hp cc đim 𝑴 trong không gian cch đim 𝑶 c định mt
khong 𝒓 > 𝟎 gi l mặt cầu tâm 𝑶, bn knh 𝒓, k hiu l: 𝑺 𝑶; 𝒓 .
Khi đó mặt cầu 𝑺 𝑶; 𝒓 = 𝑴|𝑶𝑴 = 𝒓
M
r
O
I
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN
Mặt cầu
1
Chú ý
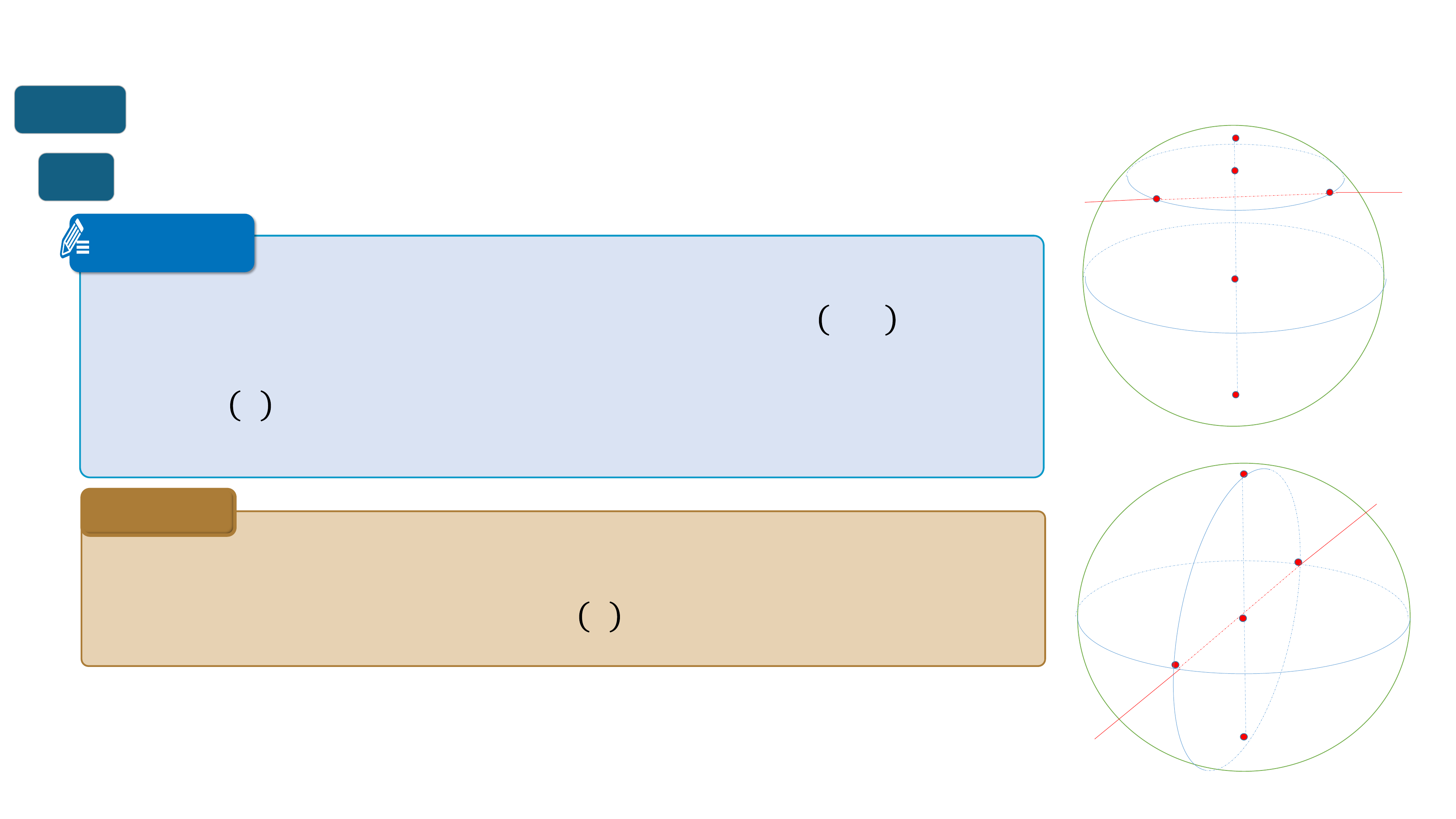
Nếu 2 đim 𝑪, 𝑫 nằm trên mặt cầu 𝑺 𝑶, 𝒓 thì
đoạn thẳng 𝑪𝑫 đưc gi là dây cung của mặt
cầu 𝑺 .
Dây cung 𝑨𝑩 đi qua tâm 𝑶 đưc gi là mt
đường kính của mặt cầu 𝑺 .
C
D
O
A
B
O
I
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN
Mặt cầu
1
Định nghĩa MC
Tp hp cc đim 𝑴 trong không gian cch đim 𝑶 c định mt
khong 𝒓 gi l mặt cầu tâm 𝑶, bn knh 𝒓, k hiu l: 𝑺 𝑶; 𝒓 . Khi đó
𝑺 𝑶; 𝒓 = 𝑴|𝑶𝑴 = 𝒓
M
r
O
Chú ý
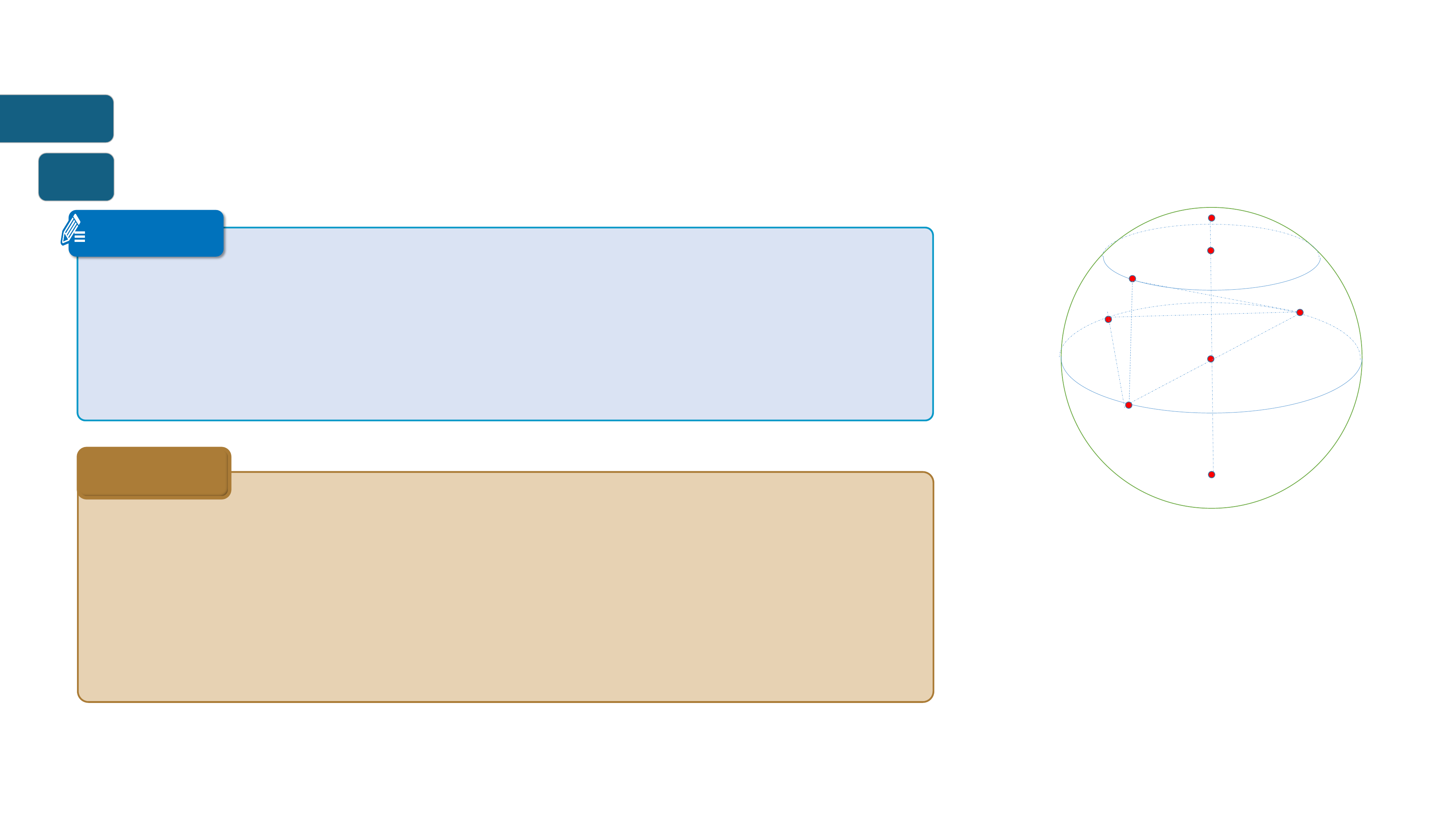
Mt mặt cầu hoàn toàn đưc xác định nếu biết tâm
và bán kính của nó hoặc biết mt đường kính của
mặt cầu đó.
I
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN
Mặt cầu
1
Ví dụ
Lời gii
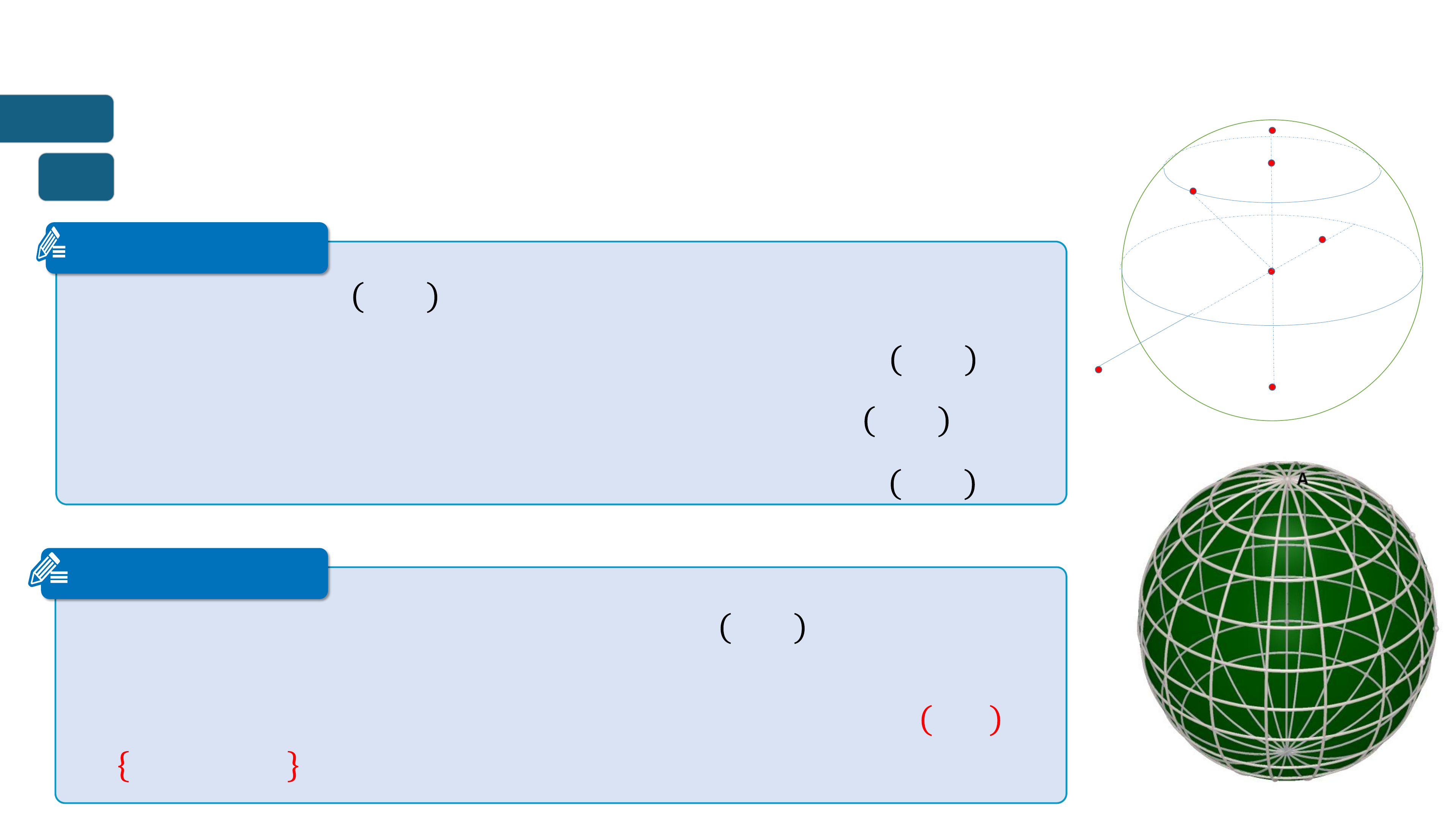
Tìm tp hp các đim 𝐌 trong không gian
luôn nhìn đoạn thẳng 𝐀𝐁 c định dưới mt góc
vuông.
Tp hp các đim 𝐌 trong không gian luôn
nhìn đoạn thẳng 𝐀𝐁 c định dưới mt góc
vuông là mặt cầu đường kính 𝐀𝐁.
M’
M
O
B
A
Định nghĩa KC
Chú ý
I
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN
Đim nằm trong, nằm ngoài mặt cầu. Khi cầu
2
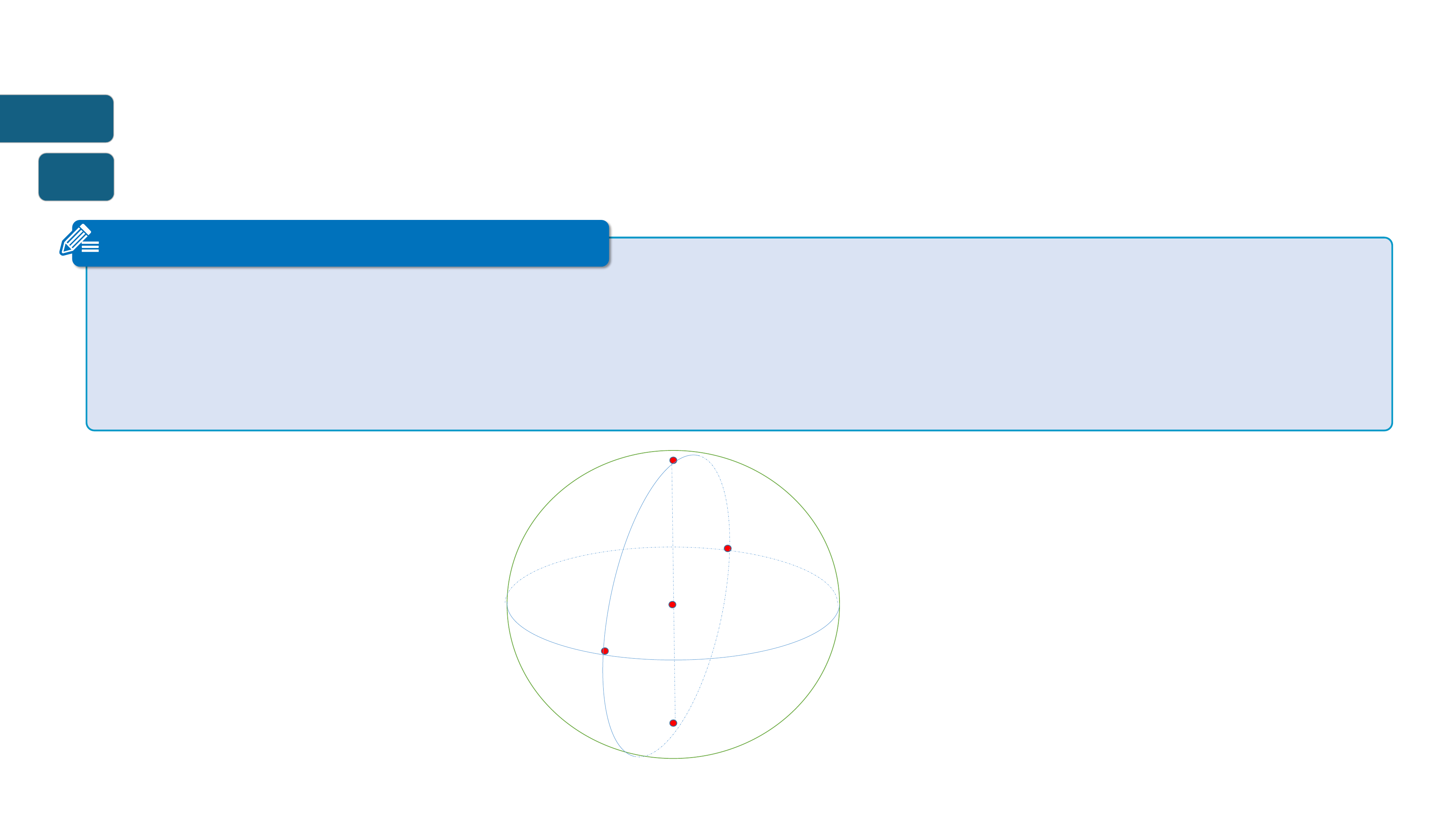
Cho mặt cầu 𝑺 𝑶; 𝑹 v mt đim 𝑨 bt k. Khi đó:
Nếu 𝑶𝑨 = 𝐑 thì ta nói đim 𝑨 trên mặt cầu 𝑺 𝑶; 𝑹 .
Nếu 𝑶𝑨 < 𝐑 𝐭𝐡ì đ𝐢ể𝐦 𝑨 nằm trong mặt cầu 𝑺 𝑶; 𝑹
Nếu 𝑶𝑨 > 𝑹 thì đim 𝑨 nằm ngoi mặt cầu 𝑺 𝑶; 𝑹 .
A
R
O
C
B
Tp hp các đim thuc mặt cầu 𝑺 𝑶; 𝑹 cùng với các
đim nằm trong mặt cầu đó đưc gi là khi cầu hoặc
hình cầu tâm 𝑶 bán kính 𝑹. Vy khi cầu 𝑺 𝑶; 𝒓 =
𝑴|𝑶𝑴 ≤ 𝒓
I
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN
Biu diễn mặt cầu
3
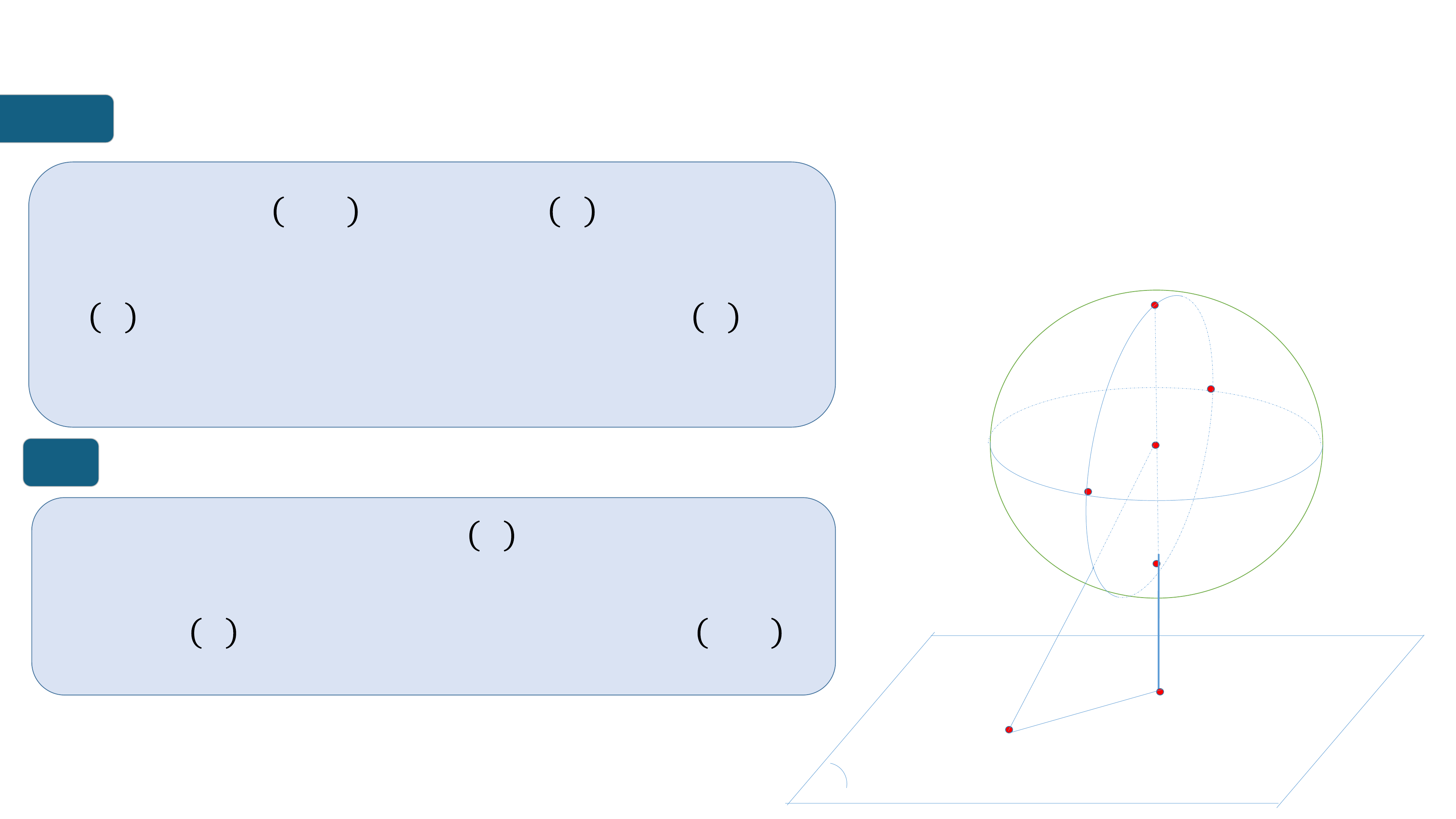
Hình biu diễn của mặt cầu là mt hình tròn.
Đ trực quan người ta vẽ thêm hình biu diễn của mt s đường tròn
nằm trên mặt cầu đó.
A
B
O
Hình biu diễn của mặt cầu
II
GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG ( Hướng dẫn tự hc)
Cho mặt cầu 𝑺 𝑶; 𝑹 v mt 𝒎𝒑 𝑷 .
Gi 𝒉 l khong cch tư tâm 𝑶 của mặt cầu đến
𝒎𝒑 𝑷 v 𝑯 l hnh chiếu của 𝑶 trên 𝒎𝒑 𝑷
𝐒𝐮𝐲 𝐫𝐚, 𝒉 = 𝑶𝑯
.
𝑀
𝐻
𝑂
𝑃
Trường hp 𝒉 > 𝑹
1
Ly mt đim bt kì 𝑴 𝑷 thì 𝑶𝑴 > 𝑶𝑯.
Từ đó suy ra 𝑶𝑴 > 𝑹.
Do đó, 𝑷 không có đim chung với 𝑺 𝑶; 𝑹 .
II
GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG ( Hướng dẫn tự hc)
Trường hp 𝒉 = 𝑹
1
Khi đó, với 𝑴 𝑷 , 𝑴 khác 𝑯
thì ta luôn có 𝑶𝑴 > 𝑶𝑯 = 𝑹 nên 𝑶𝑴 > 𝑹.
Nếu 𝒉 = 𝑹 thì đim 𝑯 𝑺 𝑶; 𝑹 .
Ta nói 𝒎𝒑 𝑷 tiếp xúc với 𝑺 𝑶; 𝑹 .
𝑯: Tiếp đim của 𝑺 𝑶; 𝑹 v 𝑷 .
𝑷 : Mặt phẳng tiếp xc hay tiếp din của 𝑺 𝑶; 𝑹 .
Vy 𝑯 là đim chung duy nht
của 𝒎𝒑 𝑷 và mặt cầu 𝑺 𝑶; 𝑹 .
𝑀
𝐻
𝑂
𝑃
NX: + 𝑷 tip xc vi mt cu 𝑺 𝑶; 𝑹 ti đim 𝑯 ⇔ 𝑷 vuông gc 𝑶𝑯 ti
đim 𝑯.
+ 𝑷 tip xc vi mt cu 𝑺 𝑶; 𝑹 ⇔ 𝒅 𝑶; (𝐏) = 𝑹.
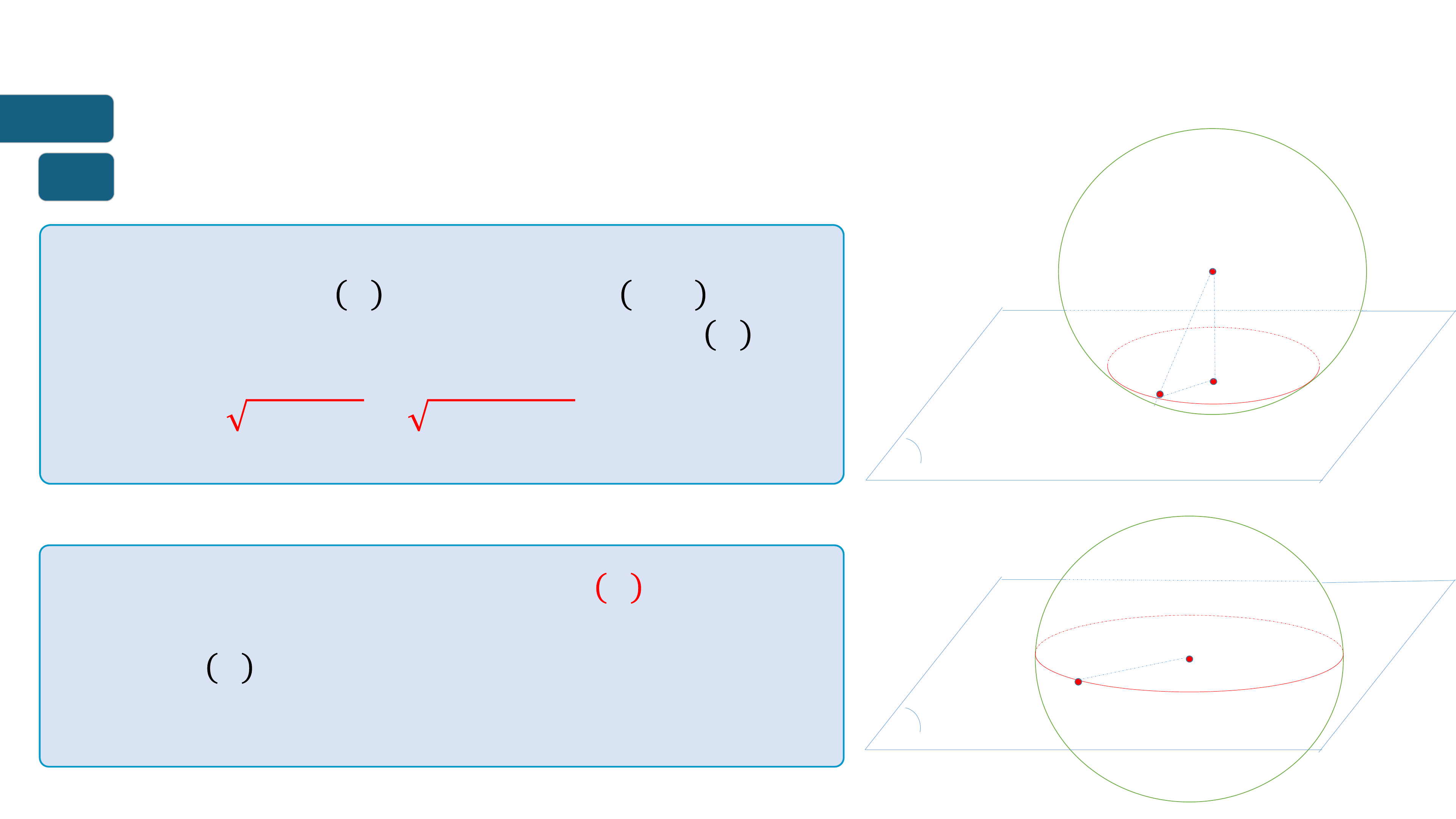
II
GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG ( Hướng dẫn tự hc)
Trường hp 𝒉 < 𝑹
1
Nếu 𝒉 < 𝑹 ⇔ 𝒎𝒑 𝑷 ct mặt cầu 𝑺 𝑶; 𝑹 theo
giao tuyến l đường trn nằm trên 𝒎𝒑 𝑷 co
tâm l 𝑯 v bn knh
𝒓 = 𝑯𝑴 = 𝑹
𝟐
− 𝒉
𝟐
= 𝑹
𝟐
− 𝑶𝑯
𝟐
𝑀
𝐻
𝑂
𝑃
𝑀
𝑂
𝑃
Đặc bit khi 𝒉 = 𝟎 mặt phẳng 𝑷 ct mặt
cầu theo mt đường tròn lớn có bán kính
𝒓 = 𝑹 và 𝑷 đưc gi là mặt phẳng kính.
III
GIAO CỦA MẶT CẦU VỚI ĐƯỜNG THẲNG. TIẾP TUYẾN
CỦA MẶT CẦU
Cho mặt cầu 𝑺 𝑶; 𝑹 va mt đường thẳng 𝜟.
Gi 𝑯 l hnh chiếu của 𝑶 trên đường thẳng
𝜟 va 𝒅 = 𝑶𝑯 l khong cch tư tâm 𝑶 của
mặt cầu đến đường thẳng 𝜟.
𝒅 > 𝑹: 𝚫 không ct mặt cầu 𝑺 𝑶; 𝑹 .
𝑀
𝑂
𝑃
𝐻
𝑂
𝑃
𝐻
𝒅 = 𝑹: 𝚫 va mặt cầu tiếp xc nhau tại H
Điu kin cần va đu đê 𝚫 tiếp xc
với 𝑺 𝑶; 𝑹 l 𝒅 = 𝒅 𝑶, 𝜟 = 𝑹.
Khi đó : H đưc gi là tiếp đim
𝚫 đưc gi là tiếp tuyến của mặt cầu (S).
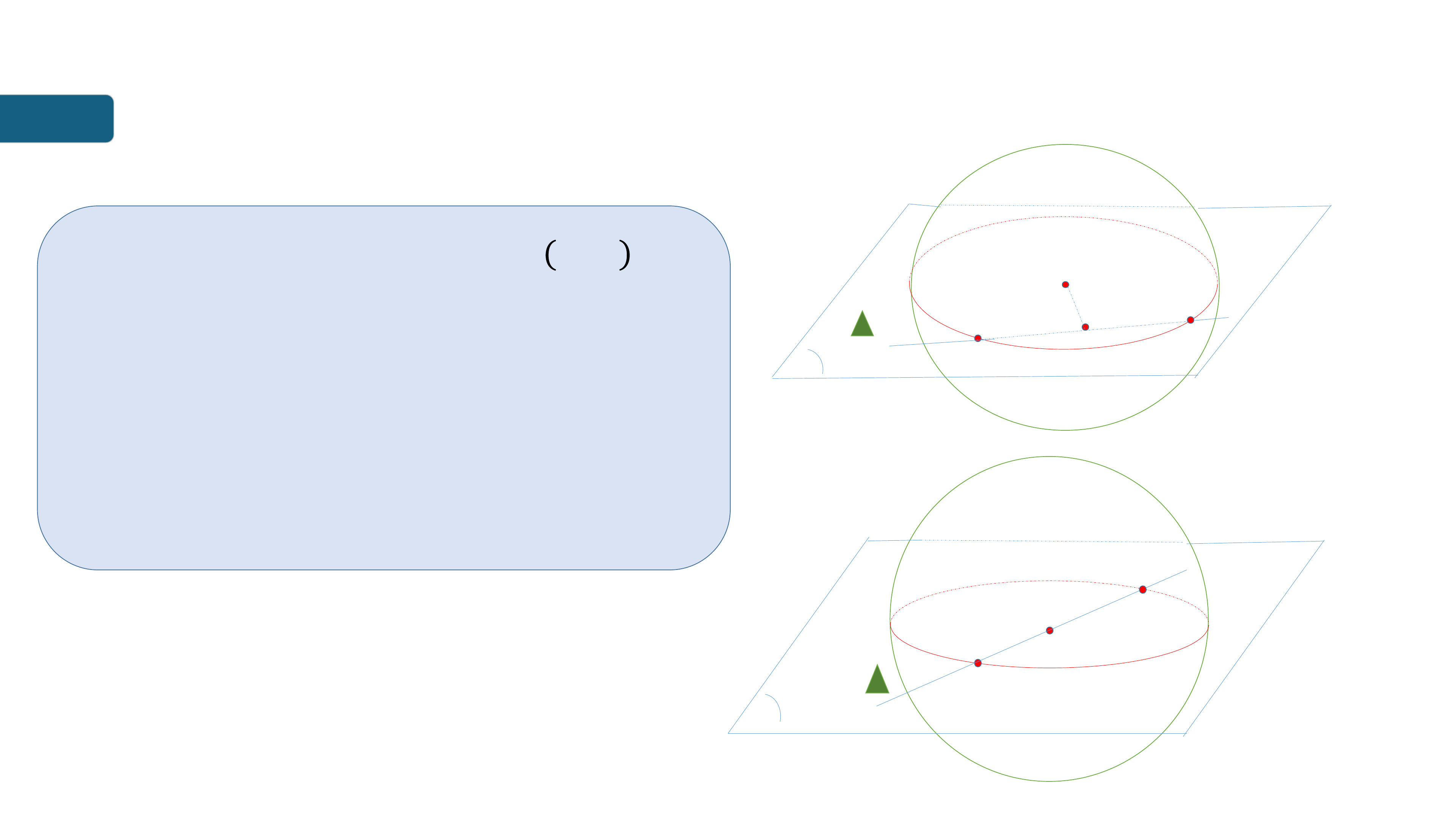
III
GIAO CỦA MẶT CẦU VỚI ĐƯỜNG THẲNG. TIẾP TUYẾN
CỦA MẶT CẦU
Nếu 𝒅 < 𝑹: 𝚫 ct mặt cầu 𝑺 𝑶; 𝑹 tại
hai đim phân bit.
𝑂
𝑃
𝑀
𝐻
𝑁
𝑂
𝑃
𝐴
𝐵
Đặc bit, khi 𝒅 = 𝟎 thi đường
thẳng 𝚫 đi qua tâm 𝑶 va ct mặt cầu
tại hai đim 𝑨, 𝑩.
Khi đo 𝑨𝑩 l đường knh của mặt
cầu.
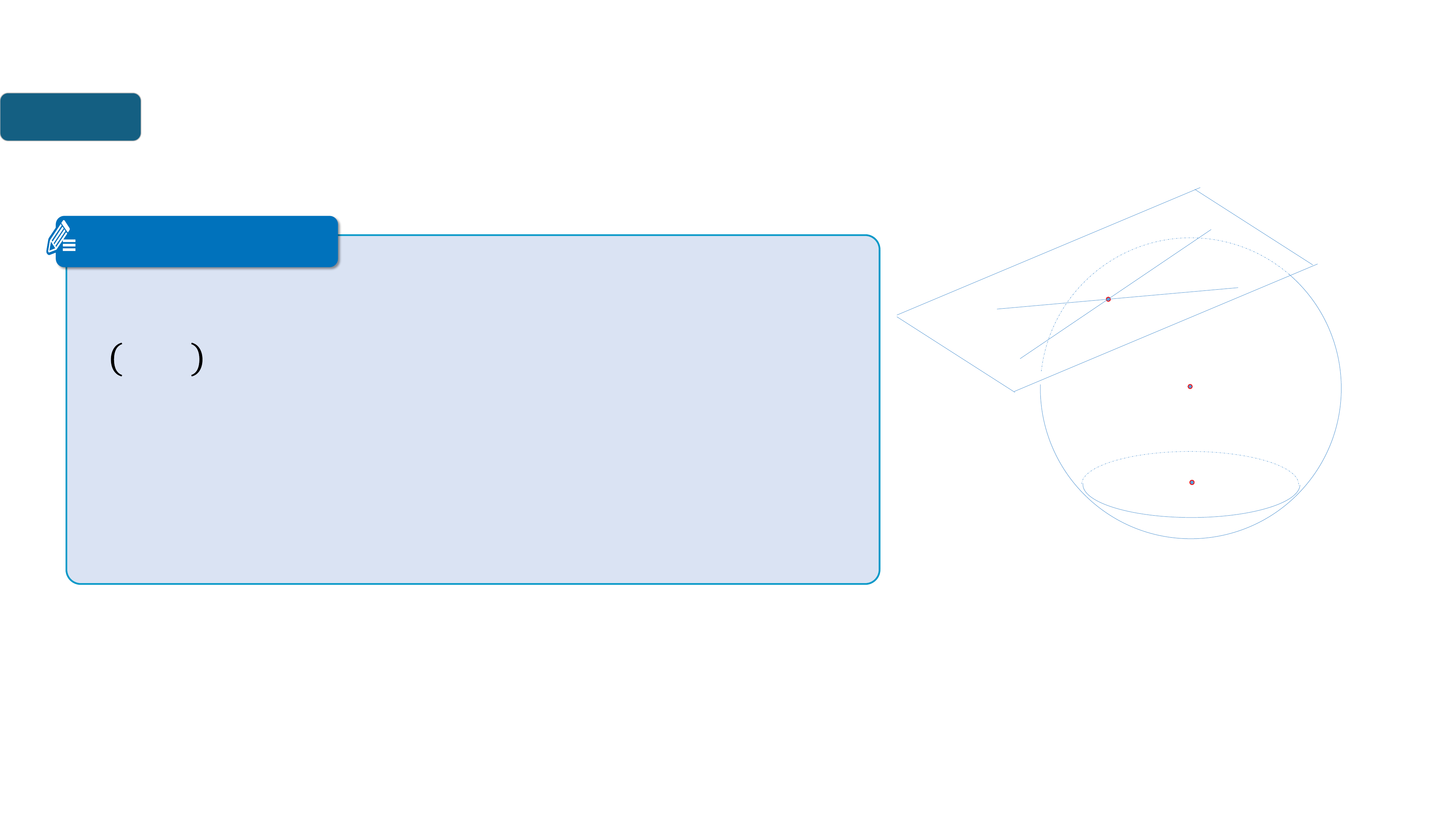
Nhn xét
III
GIAO CỦA MẶT CẦU VỚI ĐƯỜNG THẲNG. TIẾP TUYẾN
CỦA MẶT CẦU
a) Qua mt đim 𝑨 nm trên mt cu
𝑺 𝑶; 𝑹 c vô sô tip tuyn ca mt cu đo.
Tt c cc tip tuyn ny đu vuông gc vi
bn knh 𝑶𝑨 ca mt cu ti 𝑨 va đu nm
trên mt phng tip xc vi mt cu ti
đim 𝑨 đo.
𝑂
𝐴
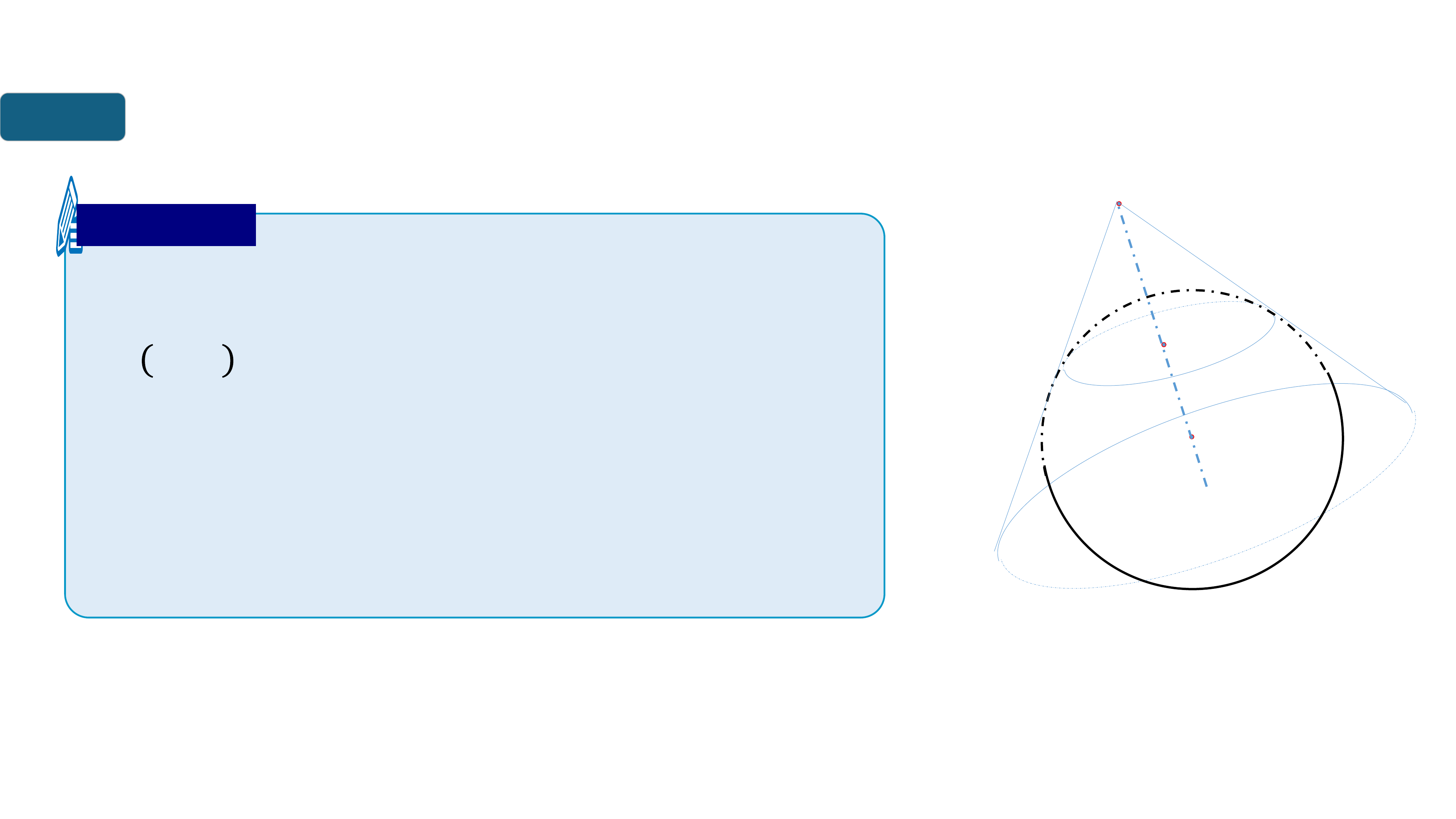
III
GIAO CỦA MẶT CẦU VỚI ĐƯỜNG THẲNG.
TIẾP TUYẾN CỦA MẶT CẦU
Nhn xét
b) Qua mt đim 𝑨 nm ngoi mt cu
𝑺 𝑶; 𝑹 c vô sô tip tuyn vi mt cu
đa cho. Cc tip tuyn ny to thnh mt
mt nn đnh 𝑨. Khi đo đô di cc đon
thng ke tư 𝑨 đn cc tip đim đu
bng nhau.
𝑂
𝐴
III
GIAO CỦA MẶT CẦU VỚI ĐƯỜNG THẲNG. TIẾP TUYẾN CỦA MẶT CẦU
Chú ý
Mặt cầu ni tiếp hnh đa din nếu mặt cầu đo tiếp xc với tt c
cc mặt của hnh đa din.
Mặt cầu ngoại tiếp hnh đa din nếu tt c cc đnh của hnh đa
din đu nằm trên mặt cầu.
Khi mặt cầu ni tiếp (ngoại tiếp) hnh đa din, người ta cng nói
hnh đa din ngoại tiếp (ni tiếp) mặt cầu.
IV
CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU VÀ THỂ TÍCH KHỐI CẦU
Mặt cầu bán kính 𝑹 có din tích là:
𝑺
𝑪
= 𝟒𝝅𝑹
𝟐
Khi cầu bán kính 𝑹 có th tích là:
𝑽
𝑪
=
𝟒
𝟑
𝝅𝑹
𝟑
DIỆN TÍCH
THỂ TÍCH
Bi gii
IV
Ví dụ
CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU VÀ THỂ TÍCH KHỐI CẦU
Mt mặt cầu 𝑺 có bán kính bằng 𝟐𝒂. Tính din tích 𝑺
𝒄
, th tích
𝑽
𝒄
của mặt cầu 𝑺 .
Th tch 𝑽
𝒄
của mặt cầu l
𝑽
𝒄
=
𝟒
𝟑
𝝅𝑹
𝟑
=
𝟒
𝟑
𝝅 𝟐𝒂
𝟑
=
𝟑𝟐
𝟑
𝝅𝒂
𝟑
.
Din tích 𝑺
𝒄
của mặt cầu là
𝑺
𝒄
= 𝟒𝝅𝑹
𝟐
= 𝟒 𝟐𝒂
𝟐
𝝅 = 𝟏𝟔𝝅𝒂
𝟐
.
Bi gii
IV
Ví dụ
CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU VÀ THỂ TÍCH KHỐI CẦU
Cho khi cầu 𝑺 có th tch bằng 𝟑𝟔𝝅 (𝐜𝒎
𝟑
). Din tch mặt
cầu bằng bao nhiêu?
Th tích khi cầu bằng 𝟑𝟔𝝅 ⇒
𝟒
𝟑
𝝅𝒓
𝟑
=
𝟑𝟔𝝅 ⇒ 𝒓
𝟑
= 𝟐𝟕 ⇒ 𝒓 = 𝟑.
Vy din tích mặt cầu 𝑺 là: 𝑺 =
𝟒𝝅𝒓
𝟐
= 𝟒𝝅. 𝟑
𝟐
= 𝟑𝟔𝝅 𝐜𝒎
𝟐
.
Bi gii
IV
Ví dụ
CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU VÀ THỂ TÍCH KHỐI CẦU
Tính th tích của khi cầu biết din tích
mặt cầu tương ứng bằng 𝟑𝟔𝝅.
Ta có: 𝑺
𝑪
= 𝟒𝝅𝑹
𝟐
= 𝟑𝟔𝝅 ⇒ 𝑹
𝟐
= 𝟗 ⇒ 𝑹 = 𝟑
⇒ 𝑽
𝑪
=
𝟒
𝟑
𝝅𝑹
𝟑
=
𝟒
𝟑
𝝅. 𝟑
𝟑
= 𝟑𝟔𝝅.
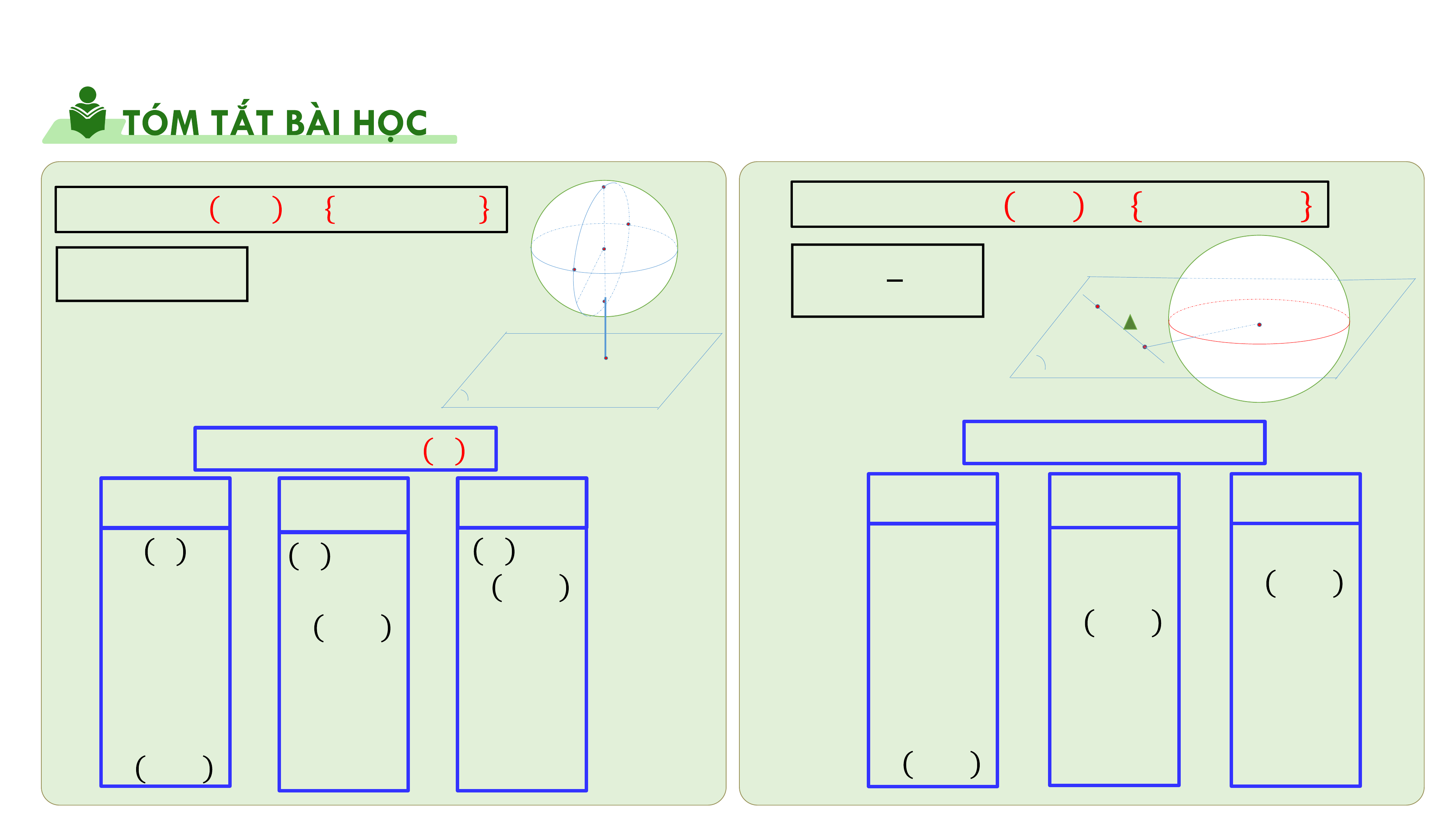
𝒉 = 𝑶𝑯 = 𝒅(𝑶; 𝑷 )
𝒉 > 𝑹 𝒉 = 𝑹 𝒉 < 𝑹
𝒉 = 𝑶𝑯 = 𝒅(𝑶; 𝚫)
𝒉 > 𝑹 𝒉 = 𝑹 𝒉 < 𝑹
𝑷
không
có
đim
chung
với
𝑺 𝑶; 𝑹
𝑷 tiếp
xúc với
𝑺 𝑶; 𝑹
𝑷 ct
𝑺 𝑶; 𝑹
theo
giao
tuyến
là đg
tròn
𝚫
không
có
đim
chung
với
𝑺 𝑶; 𝑹
𝚫 tiếp
xúc với
𝑺 𝑶; 𝑹
𝚫 ct
𝑺 𝑶; 𝑹
theo
giao
tuyến
là đg
tròn
𝐻
𝑂
𝑃
𝑀
𝑂
𝑃
𝐻
Mặt cầu 𝑺 𝑶; 𝒓 = 𝑴|𝑶𝑴 = 𝒓
Khi cầu 𝑺 𝑶; 𝒓 = 𝑴|𝑶𝑴 ≤ 𝒓
𝑺
𝑪
= 𝟒𝝅𝑹
𝟐
𝑽
𝑪
=
𝟒
𝟑
𝝅𝑹
𝟑
Nhắn tin Zalo