Trường:……………………………..
Họ và tên giáo viên: …………………………… Tổ:TOÁN
Ngày dạy đầu tiên:……………………………..
Ngày soạn: …../…../2021 Tiết:
CHƯƠNG I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT
VÀ VẼ ĐỒ THỊ HÀM SỐ
BÀI 1: SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
Môn học/Hoạt động giáo dục: Toán - GT: 12
Thời gian thực hiện: ..... tiết I. MỤC TIÊU 1. Kiến thức
- Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm này với đạo hàm.
- Nắm được qui tắc xét tính đơn điệu của hàm số.
- Biết vận dụng qui tắc để xét tính đơn điệu của một hàm số.
- Biết vận dụng tính đơn điệu của hàm số vào giải quyết các bài toán thực tế. 2. Năng lực
- Năng lực tự học: Học sinh xác định đúng đắn động cơ thái độ học tập, tự nhận ra được sai sót và khắc phục sai sót.
- Năng lực giải quyết vấn đề: Biết tiếp cận câu hỏi bài tập, biết đặt câu hỏi, phân tích các tình huống trong học tập.
- Năng lực tự quản lý: Làm chủ các cảm xúc của bản thân trong học tập và trong cuộc sống. Trưởng
nhóm biết quản lí nhóm của mình, biết phân công nhiệm vụ cho các thành viên và biết đôn đốc,
nhắc nhở các thành viên hoàn thành công việc được giao.
- Năng lực giao tiếp: Tiếp thu kiến thức trao đổi học hỏi bạn bè thông qua hoạt động nhóm
- Năng lực hợp tác: xác định nhiệm vụ của nhóm của bản thân, biết hợp tác với các thành viên trong
nhóm để hoàn thành nhiệm vụ học tập.
- Năng lực sử dụng ngôn ngữ: Biết nói và viết đúng theo ngôn ngữ Toán học.
3. Phẩm chất
- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần hợp tác xây dựng cao.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU 1
- Hình ảnh đồ thị hàm số và bảng biến thiên của hàm số 2
y = x , y = x
- Phiếu học tập số 1, số 2 và số 3.
III. TIẾN TRÌNH DẠY HỌC :
1. HOẠT ĐỘNG 1: MỞ ĐẦU a) Mục tiêu:
- Giúp HS nhớ lại khái niệm tính đồng biến, nghịch biến của hàm số.
- Giúp HS bước đầu thấy được mối liên hệ giữa tính đơn điệu và dấu của đạo hàm.
b) Nội dung: GV hướng dẫn, tổ chức học sinh ôn tập, tìm tòi các kiến thức liên quan bài học đã biết. Câu hỏi:
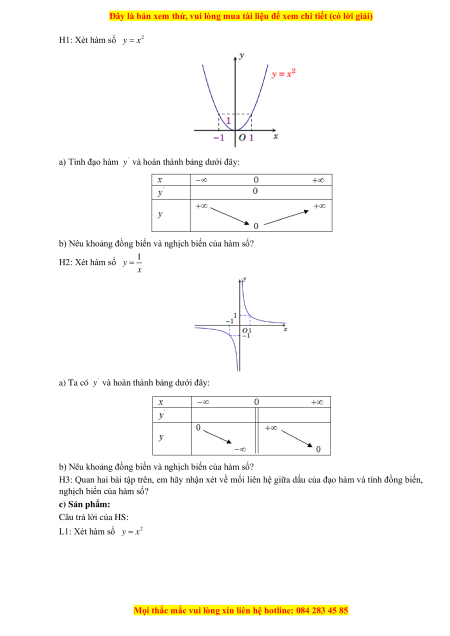
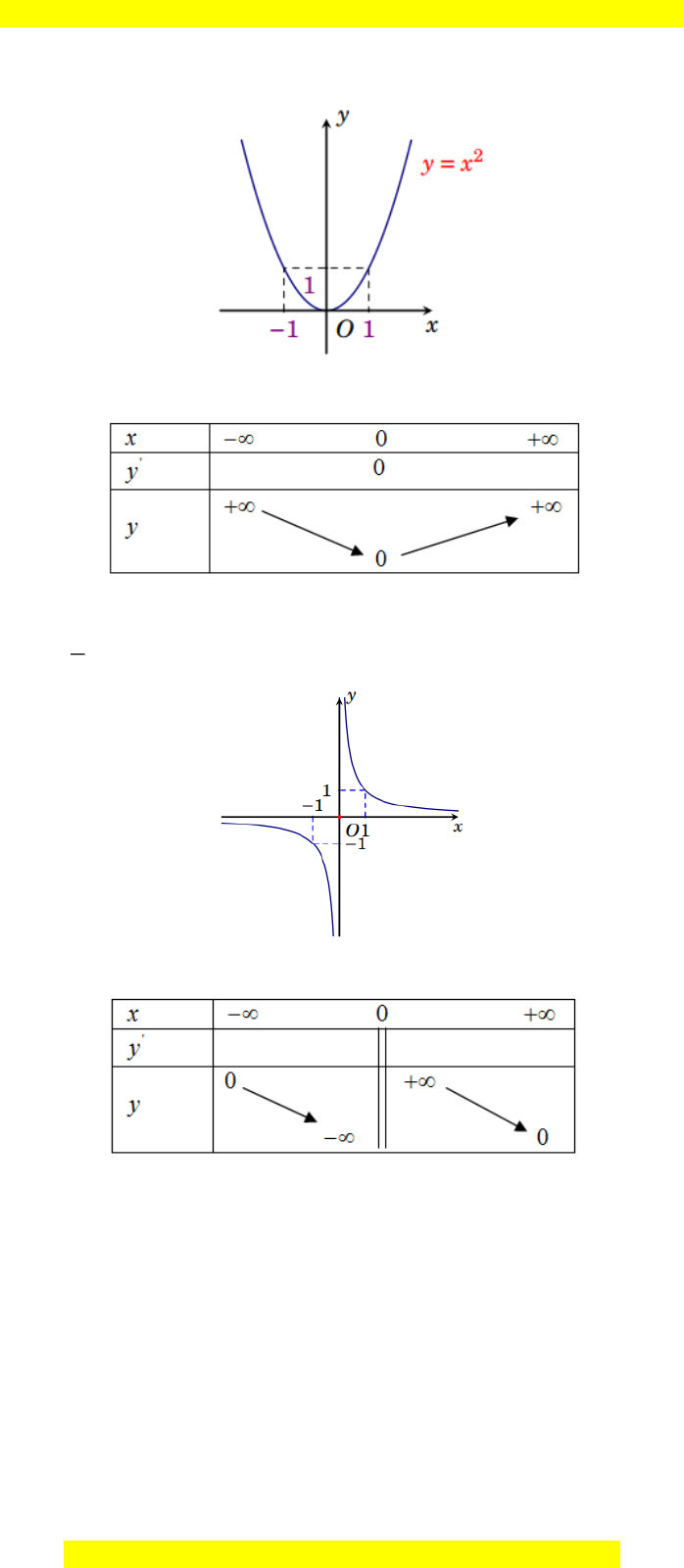
H1: Xét hàm số 2 y = x a) Tính đạo hàm '
y và hoàn thành bảng dưới đây:
b) Nêu khoảng đồng biến và nghịch biến của hàm số? H2: Xét hàm số 1 y = x a) Ta có '
y và hoàn thành bảng dưới đây:
b) Nêu khoảng đồng biến và nghịch biến của hàm số?
H3: Quan hai bài tập trên, em hãy nhận xét về mối liên hệ giữa dấu của đạo hàm và tính đồng biến,
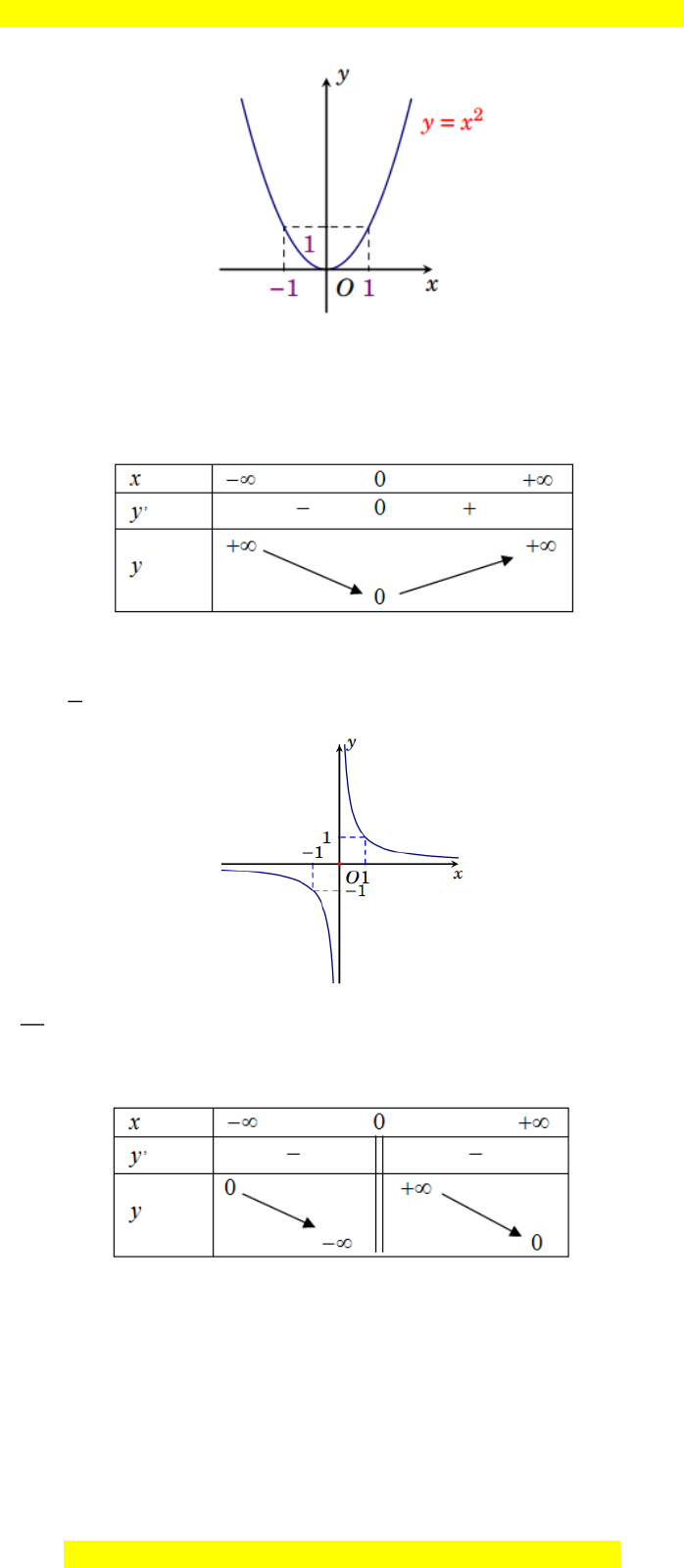
nghịch biến của hàm số? c) Sản phẩm: Câu trả lời của HS: L1: Xét hàm số 2 y = x
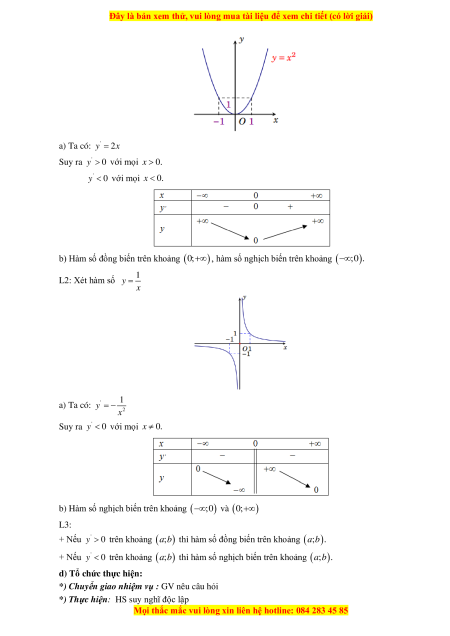
a) Ta có: ' y = 2x Suy ra '
y 0 với mọi x 0. '
y 0 với mọi x 0.
b) Hàm số đồng biến trên khoảng (0;+) , hàm số nghịch biến trên khoảng ( ; − 0). 1 L2: Xét hàm số y = x 1 a) Ta có: ' y = − 2 x Suy ra '
y 0 với mọi x 0.
b) Hàm số nghịch biến trên khoảng ( ;0 − ) và (0;+) L3: + Nếu '
y 0 trên khoảng ( ;
a b) thì hàm số đồng biến trên khoảng ( ; a b). + Nếu '
y 0 trên khoảng ( ;
a b) thì hàm số nghịch biến trên khoảng ( ; a b).
d) Tổ chức thực hiện:
*) Chuyển giao nhiệm vụ : GV nêu câu hỏi
*) Thực hiện: HS suy nghĩ độc lập
*) Báo cáo, thảo luận:
- GV gọi lần lượt 3 HS lên bảng trình bày câu trả lời của mình, mỗi học sinh 1 bài tập.
- Các học sinh khác nhận xét, bổ sung để hoàn thiện câu trả lời.
*) Đánh giá, nhận xét, tổng hợp:
- GV đánh giá thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tổng hợp kết quả.
- Dẫn dắt vào bài mới: Như vậy ngoài việc dựa vào định nghĩa hàm số đồng biến, nghịch biến, dựa
vào ĐTHS đã học ở lớp 10, chúng ta còn có một cách khác để tìm khoảng đồng biến, nghịch biến
của hàm số. Đó là dựa vào dấu của đạo hàm.
2. HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC MỚI
HOẠT ĐỘNG 2.1 I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
a) Mục tiêu: Nắm được mối liên hệ giữa dấu của đạo hàm và tính đơn điệu, lập được bảng biến thiên của hàm số
b)Nội dung: GV yêu cầu đọc SGK, trả lời câu hỏi H1, H2, giải bài toán và áp dụng làm ví dụ
H1: Nhắc lại định nghĩa tính đồng biến, nghịch biến của hàm số?
H2:Mối liên hệ giữa tính đơn điệu và dấu của đạo hàm (định lý).
H3: Ví dụ 1: Tìm các khoảng đơn điệu của hàm số: a) y = 2x −1 b) 2
y = −x + 2x
H4: Ví dụ 2: Tìm các khoảng đơn điệu của hàm số: 3 y = x c) Sản phẩm:
1. Nhắc lại định nghĩa: Cho K là khoảng, đoạn hoặc nửa khoảng. Giả sử hàm số y = f (x) xác định trên K .
y = f ( x) đồng biến trên K
x , x K : x x f x f x 1 2 1 2 ( 1) ( 2)
y = f ( x) nghịch biến trên K
x , x K : x x f x f x 1 2 1 2 ( 1) ( 2)
*Nếu hàm số đồng biến trên K thì đồ thị của nó đi lên từ trái sang phải, nếu hàm số nghịch biến
trên K thì đồ thị của nó đi xuống từ trái sang phải.
- Hoàn thành phiếu học tập số 1.
2. Tính đơn điệu và dấu của đạo hàm
Định lí: Cho hàm số y = f (x) có đạo hàm trên K .
• Nếu f (x) 0, x
K thì y = f (x) đồng biến trên K .
• Nếu f (x) 0, x
K thì y = f (x) nghịch biến trên K . Chú ý:
- Nếu f '(x) = 0, x
K thì f (x) không đổi trên K.
- Giả sử hàm số y = f ( x) có đạo hàm trên K . Nếu f ( x) 0 ( f ( x) 0 ) , x
K và f (x) = 0
chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K . VD1. a) D =
y = 2 0, x
Giáo án Toán 12 (CV 5512) | Giáo án Toán 12 mới, chuẩn nhất
449
225 lượt tải
300.000 ₫
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Bộ giáo án Toán 12 đã cập nhật đủ Cả năm.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Bộ tài liệu bao gồm: 2 tài liệu lẻ (mua theo bộ tiết kiệm đến 50%)
- Bộ giáo án Toán 12 mới, chuẩn nhất được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng bài học và bám sát chương trình Sách giáo khoa Toán 12.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(449 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 10 đề thi Cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án150.000 ₫ 1.1 K 563 lượt tải
-
Bộ 10 đề thi Cuối kì 1 Toán 12 Kết nối tri thức có đáp án150.000 ₫ 1 K 491 lượt tải
-
Bộ 10 đề thi Cuối kì 1 Toán 12 Cánh diều có đáp án150.000 ₫ 503 252 lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án150.000 ₫ 9.7 K 4.8 K lượt tải
-
Bộ 15 đề thi HSG Toán 12 có lời giải200.000 ₫ 6.9 K 3.5 K lượt tải
-
Bài giảng Powerpoint Toán 12 Kết nối tri thức350.000 ₫ 2.4 K 1.2 K lượt tải
-
Bài giảng Powerpoint Toán 12 Chân trời sáng tạo350.000 ₫ 1.2 K 622 lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 12 Chân trời sáng tạo có đáp án150.000 ₫ 2.8 K 1.4 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 12
Xem thêm-
Bộ 3 đề thi giữa kì 1 Tin học 12 Kết nối tri thức có đáp án70.000 ₫ 5 K 2.5 K lượt tải
-
Trắc nghiệm Lịch sử 12 Đúng-Sai, Trả lời ngắn (form 2025300.000 ₫ 8.2 K 4.1 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Sinh học 12 Kết nối tri thức có đáp án70.000 ₫ 4.3 K 2.2 K lượt tải
-
Bộ 5 đề thi Cuối kì 1 Tiếng Anh 12 Friends global có đáp án90.000 ₫ 426 213 lượt tải
-
Bộ 3 đề thi giữa kì 1 Sinh học 12 Chân trời sáng tạo có đáp án70.000 ₫ 1.9 K 1 K lượt tải
-
Bộ 10 đề thi giữa kì 1 Ngữ văn 12 Kết nối tri thức có đáp án150.000 ₫ 5.7 K 2.8 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Vật lí 12 Chân trời sáng tạo có đáp án70.000 ₫ 1.7 K 830 lượt tải
-
Bộ 6 đề thi giữa kì 1 Lịch sử 12 Cánh diều có đáp án100.000 ₫ 5.6 K 2.8 K lượt tải
Tài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Trường:……………………………..
Tổ:TOÁN
Ngày soạn: …../…../2021
Tiết:
Họ và tên giáo viên: ……………………………
Ngày dạy đầu tiên:……………………………..
CHƯƠNG I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT
VÀ VẼ ĐỒ THỊ HÀM SỐ
BÀI 1: SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
Môn học/Hoạt động giáo dục: Toán - GT: 12
Thời gian thực hiện: ..... tiết
I. MỤC TIÊU
1. Kiến thức
- Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm này với
đạo hàm.
- Nắm được qui tắc xét tính đơn điệu của hàm số.
- Biết vận dụng qui tắc để xét tính đơn điệu của một hàm số.
- Biết vận dụng tính đơn điệu của hàm số vào giải quyết các bài toán thực tế.
2. Năng lực
- Năng lực tự học: Học sinh xác định đúng đắn động cơ thái độ học tập, tự nhận ra được sai sót và
khắc phục sai sót.
- Năng lực giải quyết vấn đề: Biết tiếp cận câu hỏi bài tập, biết đặt câu hỏi, phân tích các tình huống
trong học tập.
- Năng lực tự quản lý: Làm chủ các cảm xúc của bản thân trong học tập và trong cuộc sống. Trưởng
nhóm biết quản lí nhóm của mình, biết phân công nhiệm vụ cho các thành viên và biết đôn đốc,
nhắc nhở các thành viên hoàn thành công việc được giao.
- Năng lực giao tiếp: Tiếp thu kiến thức trao đổi học hỏi bạn bè thông qua hoạt động nhóm
- Năng lực hợp tác: xác định nhiệm vụ của nhóm của bản thân, biết hợp tác với các thành viên trong
nhóm để hoàn thành nhiệm vụ học tập.
- Năng lực sử dụng ngôn ngữ: Biết nói và viết đúng theo ngôn ngữ Toán học.
3. Phẩm chất
- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần hợp tác xây dựng
cao.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
- Hình ảnh đồ thị hàm số và bảng biến thiên của hàm số
2
yx=
,
1
y
x
=
- Phiếu học tập số 1, số 2 và số 3.
III. TIẾN TRÌNH DẠY HỌC :
1. HOẠT ĐỘNG 1: MỞ ĐẦU
a) Mục tiêu:
- Giúp HS nhớ lại khái niệm tính đồng biến, nghịch biến của hàm số.
- Giúp HS bước đầu thấy được mối liên hệ giữa tính đơn điệu và dấu của đạo hàm.
b) Nội dung: GV hướng dẫn, tổ chức học sinh ôn tập, tìm tòi các kiến thức liên quan bài học đã
biết.
Câu hỏi:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
H1: Xét hàm số
2
yx=
a) Tính đạo hàm
'
y
và hoàn thành bảng dưới đây:
b) Nêu khoảng đồng biến và nghịch biến của hàm số?
H2: Xét hàm số
1
y
x
=
a) Ta có
'
y
và hoàn thành bảng dưới đây:
b) Nêu khoảng đồng biến và nghịch biến của hàm số?
H3: Quan hai bài tập trên, em hãy nhận xét về mối liên hệ giữa dấu của đạo hàm và tính đồng biến,
nghịch biến của hàm số?
c) Sản phẩm:
Câu trả lời của HS:
L1: Xét hàm số
2
yx=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a) Ta có:
'
2yx=
Suy ra
'
0y
với mọi
0.x
'
0y
với mọi
0.x
b) Hàm số đồng biến trên khoảng
( )
0;+
, hàm số nghịch biến trên khoảng
( )
;0 .−
L2: Xét hàm số
1
y
x
=
a) Ta có:
'
2
1
y
x
=−
Suy ra
'
0y
với mọi
0.x
b) Hàm số nghịch biến trên khoảng
( )
;0−
và
( )
0;+
L3:
+ Nếu
'
0y
trên khoảng
( )
;ab
thì hàm số đồng biến trên khoảng
( )
;.ab
+ Nếu
'
0y
trên khoảng
( )
;ab
thì hàm số nghịch biến trên khoảng
( )
;.ab
d) Tổ chức thực hiện:
*) Chuyển giao nhiệm vụ : GV nêu câu hỏi
*) Thực hiện: HS suy nghĩ độc lập
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
*) Báo cáo, thảo luận:
- GV gọi lần lượt 3 HS lên bảng trình bày câu trả lời của mình, mỗi học sinh 1 bài tập.
- Các học sinh khác nhận xét, bổ sung để hoàn thiện câu trả lời.
*) Đánh giá, nhận xét, tổng hợp:
- GV đánh giá thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tổng hợp kết quả.
- Dẫn dắt vào bài mới: Như vậy ngoài việc dựa vào định nghĩa hàm số đồng biến, nghịch biến, dựa
vào ĐTHS đã học ở lớp 10, chúng ta còn có một cách khác để tìm khoảng đồng biến, nghịch biến
của hàm số. Đó là dựa vào dấu của đạo hàm.
2. HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC MỚI
HOẠT ĐỘNG 2.1 I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
a) Mục tiêu: Nắm được mối liên hệ giữa dấu của đạo hàm và tính đơn điệu, lập được bảng biến
thiên của hàm số
b)Nội dung: GV yêu cầu đọc SGK, trả lời câu hỏi H1, H2, giải bài toán và áp dụng làm ví dụ
H1: Nhắc lại định nghĩa tính đồng biến, nghịch biến của hàm số?
H2:Mối liên hệ giữa tính đơn điệu và dấu của đạo hàm (định lý).
H3: Ví dụ 1: Tìm các khoảng đơn điệu của hàm số: a)
21yx=−
b)
2
2y x x= − +
H4: Ví dụ 2: Tìm các khoảng đơn điệu của hàm số:
3
yx=
c) Sản phẩm:
1. Nhắc lại định nghĩa: Cho
K
là khoảng, đoạn hoặc nửa khoảng. Giả sử hàm số
( )
y f x=
xác
định trên
K
.
( )
y f x=
đồng biến trên
K
( ) ( )
1 2 1 2 1 2
,:x x K x x f x f x
( )
y f x=
nghịch biến trên
K
( ) ( )
1 2 1 2 1 2
,:x x K x x f x f x
*Nếu hàm số đồng biến trên
K
thì đồ thị của nó đi lên từ trái sang phải, nếu hàm số nghịch biến
trên
K
thì đồ thị của nó đi xuống từ trái sang phải.
- Hoàn thành phiếu học tập số 1.
2. Tính đơn điệu và dấu của đạo hàm
Định lí: Cho hàm số
( )
y f x=
có đạo hàm trên
K
.
• Nếu
( )
0,f x x K
thì
( )
y f x=
đồng biến trên
K
.
• Nếu
( )
0,f x x K
thì
( )
y f x=
nghịch biến trên
K
.
Chú ý:
- Nếu
'( ) 0,f x x K=
thì
()fx
không đổi trên K.
- Giả sử hàm số
( )
y f x=
có đạo hàm trên
K
. Nếu
( )
0fx
(
( )
0fx
)
, xK
và
( )
0fx
=
chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên
K
.
VD1.
a)
D =
2 0,yx
=
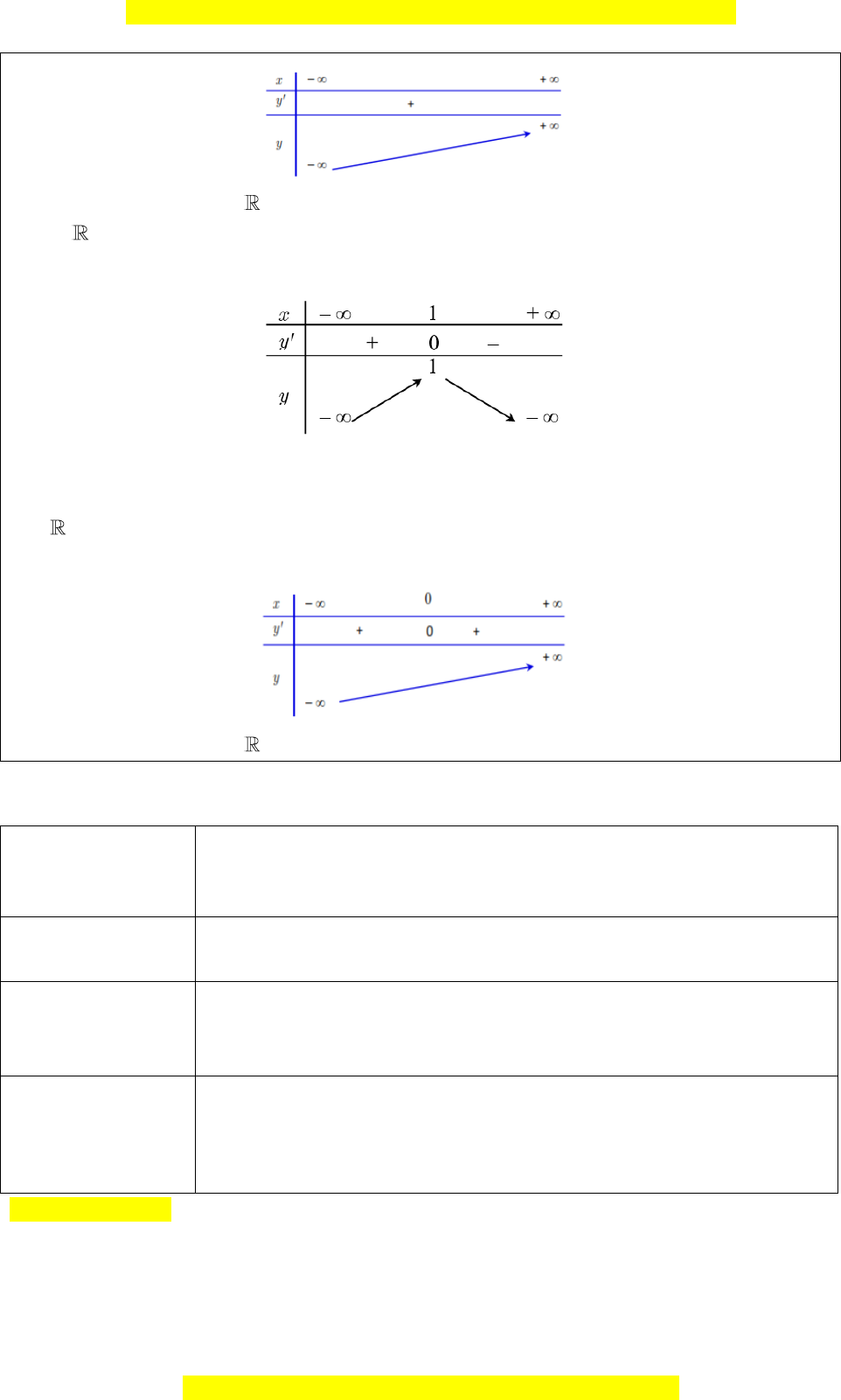
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy hàm số đồng biến trên .
b)
D =
2 2; ' 0 1y x y x
= − + = =
Vậy hàm số đồng biến trên khoảng
( )
;1−
và nghịch biến trên khoảng
( )
1; +
.
Ví dụ 2.
D =
2
3 ; ' 0 0y x y x
= = =
Vậy hàm số đồng biến trên .
d) Tổ chức thực hiện
Chuyển giao
- Từ Hoạt động 1, học sinh thảo luận về mối liên hệ giữa tính đơn điệu và
dấu của đạo hàm.
- Học sinh thảo luận theo cặp giải các ví dụ 1, ví dụ 2.
Thực hiện
- HS thảo luận theo nhóm.
GV theo dõi, hỗ trợ , hướng dẫn các nhóm
Báo cáo thảo luận
- HS nêu bật được mối liên hệ giữa tính đơn điệu và dấu của đạo hàm.
- GV gọi 2HS lên bảng trình bày lời giải cho VD1 và VD2
- HS khác theo dõi, nhận xét, hoàn thiện sản phẩm
Đánh giá, nhận xét,
tổng hợp
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo
- Chốt kiến thức và các bước thực hiện xét tính đơn điệu của hàm số.
HOẠT ĐỘNG 2.2 II. QUY TẮC XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
a) Mục tiêu: Hình thành các bước và biết cách xét tính đơn điệu của hàm số .
b)Nội dung:
Học sinh đọc sách giáo khoa và nêu các bước xét tính đơn điệu của hàm số, sau đó áp dụng làm
ví dụ 3
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ví dụ 3: : Xét sự đồng biến, nghịch biến của hàm số
a)
3
32y x x= − +
b)
1
1
x
y
x
−
=
+
c)
42
22y x x= − +
c) Sản phẩm:
1. Quy tắc
B1. Tìm tập xác định.
B2.Tính
( )
fx
. Tìm các điểm tại đó
( )
0fx
=
hoặc
( )
fx
không xác định.
B3. Lập bảng biến thiên.
B4. Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
2. Áp dụng: Ví dụ 3
a) Hàm số ĐB trên
( )
;1− −
và
( )
1; +
. Hàm số NB trên
( )
1;1−
.
b) Hàm số ĐB trên
( )
;1− −
và
( )
1;− +
.
c) Hàm số NB trên
( )
;1− −
và
( )
0;1
. Hàm số ĐB trên
( )
1;0−
và
( )
1; .+
d) Tổ chức thực hiện
Chuyển giao
- Từ ví dụ 1 và 2, HS thảo luận và nêu các bước xét tính đơn điệu của hàm
số.
- Các cặp đôi thảo luận ví dụ 3.
Thực hiện
- HS thảo luận cặp đôi thực hiện nhiệm vụ.
- GV quan sát, theo dõi các nhóm. Giải thích các thắc mắc nếu có của HS.
Báo cáo thảo luận
- Các cặp thảo luận đưa ra các bước xét tính đơn điệu của hàm số.
- Thực hiện được VD3.
- Thuyết trình các bước thực hiện.
- Các nhóm khác nhận xét hoàn thành sản phẩm
Đánh giá, nhận xét,
tổng hợp
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
và tuyên dương nhóm học sinh có câu trả lời tốt nhất.
- Trên cơ sở câu trả lời của học sinh, GV kết luận các bước xét tính đơn
điệu của hàm số.
3. HOẠT ĐỘNG 3: LUYỆN TẬP
Hoạt động 3.1. Rèn luyện kỹ năng giải bài tập tự luận về xét tính đơn điệu của hàm số
và áp dụng tính đơn điệu của hàm số để chứng minh các bất đẳng thức
a) Mục tiêu:
- Học sinh làm được một số dạng toán tự luận về xét tính đơn điệu của hàm số.
- Ứng dụng được tính đơn điệu của hàm số để chứng minh bất đẳng thức.
b) Nội dung: Học sinh làm các bài tập tự luận sau:
PHIẾU HỌC TẬP SỐ 1
Bài 1. Xét tính đồng biến, nghịch biến của các hàm số:
a)
2
43y x x= + −
b)
32
1
3 7 2
3
y x x x= + − −
c)
42
23y x x= − +
d)
32
5y x x= − + −
Bài 2: Tìm các khoản đơn điệu của các hàm số:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a)
31
1
x
y
x
+
=
−
b)
2
2
1
xx
y
x
−
=
−
c)
2
20y x x= − −
d)
2
2
9
x
y
x
=
−
Bài 3: Chứng minh rằng hàm số
2
1
x
y
x
=
+
đồng biến trên khoảng
( 1;1)−
; nghịch biến trên các
khoảng
( ; 1)− −
và
(1; )+
.
Bài 4: Chứng minh rằng hàm số
2
2y x x=−
đồng biến trên khoảng
(0;1)
và nghịch biến trên
khoảng
(1;2)
.
Bài 5: Chứng minh các bất đẳng thức sau:
a) tan
x
>
x
b)
3
tan 0
32
x
x x x
+
c) Sản phẩm:
- Học sinh thể hiện bài tập tự luận (Phiếu học tập số 1) trên bảng nhóm kết quả bài làm của
mình.
- Dự kiến sản phẩm của các nhóm như sau:
Bài 1.
a)
2
43y x x= + −
Tập xác định : D= ; Đạo hàm:
32yx
=−
;
3
'0
2
yx= =
Bảng biến thiên
Vậy hàm số đồng biến trên khoảng
3
;
2
−
và nghịch biến trên khoảng
3
;
2
+
b) b)
32
1
3 7 2
3
y x x x= + − −
Hàm số đồng biến trên các khoảng
( )
;7− −
,
( )
1; +
và nghịch biến trên khoảng
( )
7;1−
c)
42
23y x x= − +
Hàm số đồng biến trên các khoảng
( ) ( )
1;0 , 1;− +
và nghịch biến trên các khoảng
( ) ( )
; 1 , 0;1− −
d)
32
5y x x= − + −
Hàm số đồng biến trên các khoảng
2
0;
3
và nghịch biến trên các khoảng
( )
2
;0 , ;
3
− +
Bài 2:
a)
31
1
x
y
x
+
=
−
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Tập xác định : D= ;
( )
2
4
' 0, 1
1
yx
x
=
−
Vậy hàm số đồng biến trên các khoảng
( ) ( )
;1 , 1;− +
b)
2
2
1
xx
y
x
−
=
−
Tập xác định:
\1D =
;
( )
( )
( )
2
2
22
11
22
' 0, 1
11
x
xx
yx
xx
− − −
− + −
= =
−−
Vậy hàm số nghịch biến trên các khoảng
( ) ( )
;1 , 1;− +
c)
2
20y x x= − −
Đáp số: Hàm số nghịch biến trên khoảng
( )
;4− −
, đồng biến trên khoảng
(5; )+
d)
2
2
9
x
y
x
=
−
Đáp số: Hàm số nghịch biến trên các khoảng
( ) ( ) ( )
; 3 , 3;3 , 3;− − − +
.
Bài 3: Chứng minh rằng hàm số
2
1
x
y
x
=
+
đồng biến trên khoảng
( 1;1)−
; nghịch biến trên các
khoảng
( ; 1)− −
và
(1; )+
.
Tập xác định:
D =
;
( )
2
2
2
1
1
x
y
x
−
=
+
;
1
0
1
x
y
x
=
=
=−
Bảng biến thiên
Bài 4: Hàm số xác định trên
0;2D =
2
1
'
2
x
y
xx
−
=
−
Bảng biến thiên:
Hàm số đồng biến trên khoảng
( )
0;1
và nghịch biến trên khoảng
( )
1;2
Bài 5:
a)
tanxx
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Xét hàm số g(
x
) = tan
x
-
x
xác định với các giá trị
x
0;
2
Ta có: g’(
x
) = tan
2
x
0
x
0;
2
và g'(
x
) = 0 chỉ tại điểm
x
= 0 nên hàm số g(
x
)
đồng biến trên
0;
2
Do đó
( ) (0) 0g x g=
,
x
0;
2
Vậy
tanxx
,
x
0;
2
b)
3
tan 0
32
x
x x x
+
Đặt g(
x
)=
3
tan , 0;
32
x
x x x
− −
Tacó: g’(
x
)=
( )( )
22
tan tan tan 0x x x x x x− = − +
Trên
0;
2
g'(
x
) = 0 chỉ tại điểm
x
= 0 nên hàm số g(
x
) đồng biến trên
0;
2
Do đó:
( ) (0) 0g x g=
,
x
0;
2
Vậy
3
tan 0
32
x
x x x
+
d) Tổ chức thực hiện
Chuyển giao
GV: Chia lớp thành 4 nhóm, tổ chức, giao nhiệm vụ như sau :
+ Nhóm 01 : Làm câu a, b của bài tập 1 và Bài tập 3.
+ Nhóm 02 : Làm câu c, d của bài tập 1 và bài tập 4.
+ Nhóm 03 : Làm câu a, b, c, d của bài tập 2.
+ Nhóm 04 : Làm bài tập 5.
HS: Nhận nhiệm vụ
Thực hiện
GV: điều hành, quan sát, hướng dẫn các nhóm thực hiện.
HS: Tập hợp theo nhóm và thực hiện nhiệm vụ được phân công.
Báo cáo thảo luận
- Đại diện 04 nhóm trình bày kết quả thảo luận.
- Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn
các vấn đề
Đánh giá, nhận xét,
tổng hợp
- GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh,
ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. Chốt lại
kiến thức và yêu cầu học sinh ghi nhận kiến thức.
- Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo
Hoạt động 3.2. Rèn luyện kỹ năng giải bài tập trắc nghiệm về xét tính đơn điệu của hàm số.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a) Mục tiêu:
- Học sinh làm được một số dạng toán trắc nghiệm về xét tính đơn điệu của hàm số.
b) Nội dung: Học sinh làm các bài tập trắc nghiệm sau:
PHIẾU HỌC TẬP SỐ 2
Câu 1. (K tra định kỳ THPT Nguyễn Khuyến Lần 1_2020) Cho hàm số
()y f x=
có đồ thị như
hình vẽ
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( ;0)−
và
( )
2;+
. B.
( ;1)−
và
( )
4;+
. C.
(1;4)
. D.
(0;2)
.
Câu 2. (Thuận Thành 2- Bắc Ninh- lần 1) Cho hàm số
( )
fx
có đạo hàm
( ) ( )
3
3f x x x
=−
, với
mọi
x
thuộc . Hàm số đã cho đồng biến trên khoảng nào sau đây?
A.
( )
1;0−
. B.
( )
0;3
. C.
( )
2;1−
. D.
( )
1;3
.
Câu 3. (Yên Lạc-Vĩnh Phúc-Lần 1-Năm 2019-2020) Cho hàm số
( )
y f x=
có bảng xét dấu của
đạo hàm như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
( )
;0−
. B. Hàm số nghịch biến trên khoảng
( )
0;2
.
C. Hàm số đồng biến trên khoảng
( )
2;0−
. D. Hàm số nghịch biến trên khoảng
( )
;2− −
.
Câu 4. Tìm tất cả giá trị thực của tham số
m
để hàm số
32
1
2 ( 3) 5
3
y x mx m x m= − + + + −
đồng
biến trên .
A.
3
4
m −
. B.
3
1
4
m−
. C.
1m
. D.
3
1
4
m−
.
Câu 5. (Khảo sát chất lượng cuối học kì 1) Cho hàm số
59
1
x
y
x
+
=
−
. Khẳng định nào sau đây là
đúng?
A. Hàm số nghịch biến trên
\1
. B. Hàm số đồng biến trên
( ) ( )
;1 1;− +
.
C. Hàm số nghịch biến trên
( )
;1−
và
( )
1; +
. D. Hàm số nghịch biến trên
( ) ( )
;1 1;− +
.
Câu 6. (Chuyên Bắc Ninh - Lần 2 - 2020) Cho hàm số
( )
y f x=
xác định
\0
, liên tục trên
từng khoảng xác định và có bảng biến thiên như hình vẽ:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
( )
1;− +
. B. Hàm số nghịch biến trên
( )
0;1
.
C. Hàm số nghịch biến trên khoảng
( )
1;1−
. D. Hàm số đồng biến trên khoảng
( )
1;0−
.
Câu 7. (Trần Phú - Quảng Ninh - Lần 2 - 2020) Cho hàm số
()y f x=
có bảng biến thiên như hình
sau
Hàm số
()y f x=
đồng biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
2;0−
. C.
( )
2;− +
. D.
( )
0;2
.
Câu 8. (Yên Lạc-Vĩnh Phúc-Lần 1-Năm 2019-2020) Cho hàm số
42
y ax bx c= + +
có đồ thị như
hình vẽ.
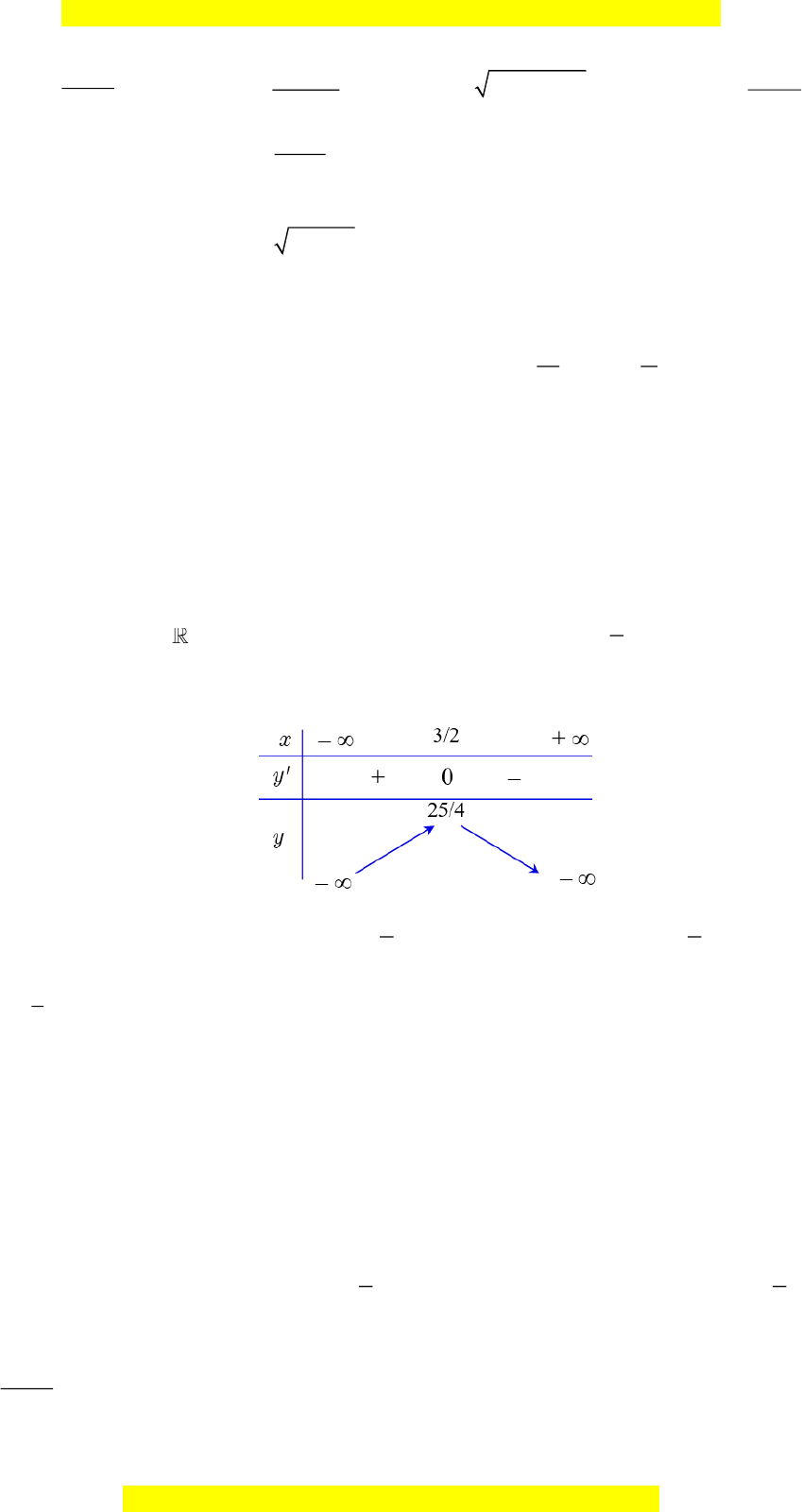
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
1; +
B.
( )
1;1−
C.
( )
0;1
D.
( )
;1− −
Câu 9. (THPT Chuyên Hạ Long - QNinh - Lần 1 - 2017 - 2018 - BTN) Hàm số
32
31y x x= − + +
đồng biến trên khoảng nào dưới đây?
A.
( )
;0−
và
( )
2;+
. B.
( )
0;+
. C.
( )
0;2
. D.
( )
;2−
.
Câu 10. [CHUYÊN SƠN LA - 2017] Hàm số
2
2y x x= − +
nghịch biến trên khoảng nào ?
A.
( )
0;1
. B.
( )
1;2
. C.
( )
1; +
. D.
( )
;1−
.
Câu 11. Tất cả các giá trị thực của tham số
m
sao cho hàm số
42
(2 3)y x m x m= − + − +
nghịch
biến trên khoảng
( )
1;2
là
;
p
q
−
, trong đó phân số
p
q
tối giản và
0q
. Hỏi tổng
pq+
là?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
3
. B.
5
. C.
9
. D.
7
.
Câu 12. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
6+−
=
−
xm
y
xm
đồng biến
trên
( )
;2− −
?
A.
4
. B.
6
. C.
5
. D.
3
.
Câu 13. Hàm số nào đồng biến trên khoảng
( )
;− +
.
A.
42
21= − + +y x x
. B.
1
1
x
y
x
−
=
+
. C.
1yx=+
. D.
3
2y x x= + −
.
Câu 14. [NB-BTN-2017] Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
tan 2
tan
x
y
xm
−
=
−
đồng biến trên khoảng
0;
4
?
A.
2m
. B.
0m
. C.
12m
. D.
0;1 2mm
.
Câu 15. Cho hàm số
2015 2016mx m
y
xm
++
=
−−
với
m
là tham số thực. Gọi
S
là tập hợp các giá trị
nguyên của
m
để hàm số đồng biến trên từng khoảng xác định. Tính số phần tử của
S
.
A.
2015
. B.
2018
. C.
2016
. D.
2017
.
Câu 16. Cho
32
1
2 2019
3
y x x mx= − + + −
. Có bao nhiêu giá trị nguyên dương của
m
để hàm số
nghịch biến trên
1;2
.
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 17. (THPT Trần Nhân Tông - Quảng Ninh - Lần 1 - 2017 - 2018 - BTN) Cho hàm số
()y f x=
có đồ thị như hình vẽ. Hỏi hàm số
2
(2 )y f x=−
đồng biến trên khoảng nào sau đây?
A.
( )
0;1
. B.
( )
1;0−
. C.
( )
2;1−
. D.
( )
1; +
.
Câu 18. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số
43
( ) 2018, ( ) 2 2018f x x g x x= + = −
và
21
()
1
x
hx
x
−
=
+
. Trong các hàm số đã cho, có tất cả bao nhiêu
hàm số không có khoảng nghịch biến?
A. 0. B. 3. C. 2. D. 1.
Câu 19. [SỞ GDĐT LÂM ĐỒNG LẦN 03 - 2017] Tìm tất cả các giá trị thực của tham số
m
sao
cho hàm số
2
cos
sin
−
=
mx
y
x
nghịch biến trên
;
32
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
0m
. B.
2m
. C.
5
4
m
. D.
1m
.
Câu 20. (CHUYÊN VINH LẦN 3-2018) Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
y f x
=
được cho như hình bên. Hàm số
( )
2
22y f x x= − − +
nghịch biến trên khoảng
A.
( )
2; 1−−
. B.
( )
1; 0−
. C.
( )
0; 2
. D.
( )
3; 2−−
.
Câu 21. (Trần Phú - Quảng Ninh - Lần 2 - 2020) Cho hàm số
( )
fx
có bảng xét dấu của đạo hàm
như sau
Hàm số
( )
3
2
2 1 8 5
3
y f x x x= + + − +
nghịch biến trên khoảng nào dưới đây?
A.
( )
;2− −
. B.
( )
1;+
. C.
( )
1;7−
. D.
1
1;
2
−
.
Câu 22. (THPT Đội Cấn - 2020) Tổng tất cả các giá trị của tham số
m
để hàm số
( )
2 5 3 2 2
11
10 20 1
53
y m x mx x m m x= − + − − − +
đồng biến trên bằng
A.
5
2
. B.
2−
. C.
1
2
. D.
3
2
.
Câu 23. (Chuyên Thái Bình - Lần 1 – 2020
Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( )
2
3
91f x x x x
= − −
. Hàm số
( )
2
y f x=
nghịch biến trên khoảng nào sau đây?
A.
( )
;3− −
. B.
( )
1;1−
. C.
( )
3;0−
. D.
( )
3; +
.
Câu 24. Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
32
12 2y x mx x m= − + +
luôn đồng
biến trên khoảng
( )
1; +
?
A.
21
. B.
20
. C.
18
. D.
19
.
Câu 25. (Đề tốt nghiệp THPT 2020 mã đề 103) Cho hàm số bậc bốn
()fx
có bảng biên thiên như
sau:
Số điểm cực trị của hàm số
42
( ) [ ( 1)]g x x f x=−
là
3
2
3
−
2
−
1
4
1
5
O
x
y
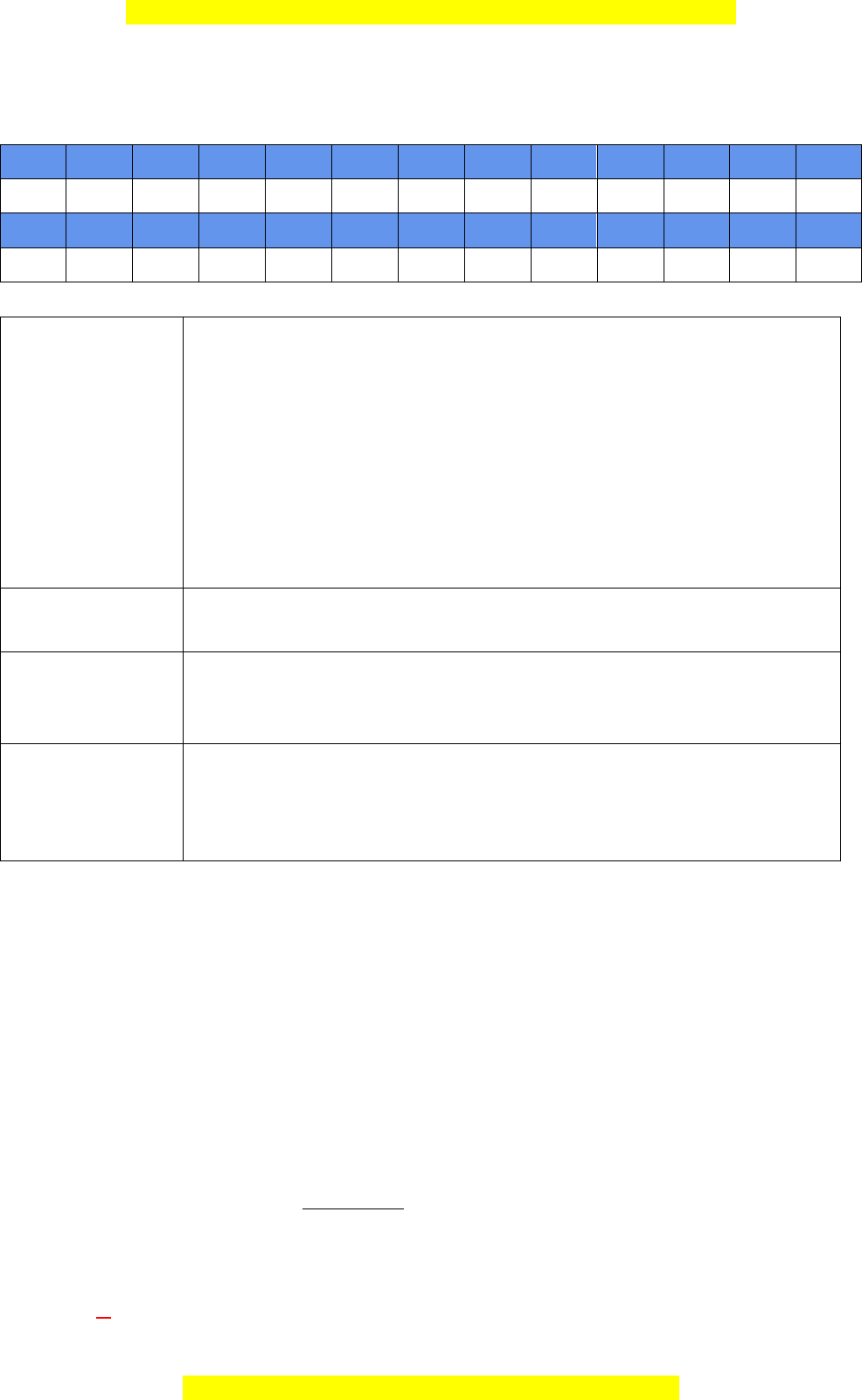
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
7
. B.
5
. C.
9
. D.
11
.
c) Sản phẩm:
- Đáp án bài tập trắc nghiệm trong phiếu học tập số 2 của học sinh:
1
2
3
4
5
6
7
8
9
10
11
12
13
D
A
B
B
C
B
D
A
C
B
D
A
D
14
15
16
17
18
19
20
21
22
23
24
25
D
C
A
A
C
C
B
D
C
A
B
C
d) Tổ chức thực hiện
Chuyển giao
GV: Tổ chức lớp theo 06 nhóm. Yêu cầu các nhóm cùng thực hiện các bài
tập trắc nghiệm trên như sau :
+ Nhóm 1 : làm các câu 1, 2, 3, 24, 25.
+ Nhóm 2: làm các câu 4, 5, 22, 23.
+ Nhóm 3 : làm các câu 6, 7, 20, 21.
+ Nhóm 4 : làm các câu 9, 9, 18, 19.
+ Nhóm 5 : làm các câu 10, 11, 16, 17.
+ Nhóm 6 : làm các câu 12, 13, 14, 15.
HS: Nhận các nhóm nhiệm vụ
Thực hiện
- GV: điều hành, quan sát, hướng dẫn các nhóm thực hiện nhiệm vụ.
- HS: Các nhóm tập trung và thực hiện nhiệm vụ được giao.
Báo cáo thảo luận
- Đại diện nhóm trình bày kết quả thảo luận.
- Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ
hơn các vấn đề
Đánh giá, nhận xét,
tổng hợp
- GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh,
ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. Chốt lại
kiến thức cho học sinh.
- Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo
4. HOẠT ĐỘNG 4: VẬN DỤNG.
a)Mục tiêu: Giải quyết một số bài toán ứng dụng tính đơn điệu của hàm số trong thực tế.
b) Nội dung:
PHIẾU HỌC TẬP SỐ 3
Vận dụng 1:
Theo thống kê tại một nhà máy
Z
, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100
công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm
việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1
công nhân/1 giờ (và như vậy, nếu giảm thời gian làm việc 2 giờ mỗi tuần thì sẽ có thêm 1 công
nhân đi làm đồng thời năng suất lao động tăng 5 sản phẩm/1 công nhân/1 giờ). Ngoài ra, số phế
phẩm mỗi tuần ước tính là
( )
2
95 120
4
xx
Px
+
=
, với
x
là thời gian làm việc trong một tuần. Nhà
máy cần áp dụng thời gian làm việc mỗi tuần mấy giờ để số lượng sản phẩm thu được mỗi tuần là
lớn nhất?
A.
36.x =
B.
32.x =
C.
44.x =
D.
48.x =
Vận dụng 2:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Một người đàn ông muốn chèo thuyền ở vị trí
A
tới điểm
B
về phía hạ lưu bờ đối diện,
càng nhanh càng tốt, trên một bờ sông thẳng rộng
3 km
(như hình vẽ). Anh có thể chèo thuyền của
mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
, hay có thể chèo trực tiếp đến
B
, hoặc anh
ta có thể chèo thuyền đến một điểm
D
giữa
C
và
B
và sau đó chạy đến
B
. Biết anh ấy có thể
chèo thuyền
6 km/ h
, chạy
8 km/ h
và quãng đường
8 kmBC =
. Biết tốc độ của dòng nước là
không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất (đơn
vị: giờ) để người đàn ông đến
B
.
A.
3
2
. B.
9
7
. C.
73
6
. D.
7
1
8
+
.
c) Sản phẩm: Sản phẩm trình bày của 02 nhóm học sinh
d) Tổ chức thực hiện
Chuyển giao
GV: Chia lớp thành 02 nhóm. Phát phiếu học tập số 3 vào cuối tiết luyện
tập của bài. Yêu cầu học sinh về nhà thực hiện.
HS: Nhận nhiệm vụ,
Thực hiện
Các nhóm HS thực hiện tìm tòi, nghiên cứu và làm bài ở nhà .
Chú ý: Việc tìm kết quả tích phân có thể sử dụng máy tính cầm tay.
Báo cáo thảo luận
HS cử đại diện của mỗi nhóm trình bày sản phẩm vào tiết tiếp theo.
Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn
các vấn đề.
Đánh giá, nhận xét,
tổng hợp
- GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh,
ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất.
- Chốt kiến thức tổng thể trong bài học.
- Hướng dẫn HS về nhà tự xây dựng tổng quan kiến thức đã học bằng sơ đồ
tư duy.
• Hướng dẫn làm bài trắc nghiệm trong phiếu học tập số 2 và 3:
Câu 1. Chọn D
Từ đồ thị suy ra hàm số nghịch biến trên khoảng:
(0;2)
.
Câu 2. Chọn A
( ) ( )
3
0
0 3 0
3
x
f x x x
x
=
= − =
=
.
Ta có BBT:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy hàm số đồng biến trên các khoảng
( )
;0−
và
( )
3; +
nên hàm số đồng biến trên
( )
1;0−
.
Câu 3. Chọn B
Từ bảng xét dấu của đạo hàm ta thấy
0y
,
( )
0;2x
Do đó hàm số nghịch biến trên khoảng
( )
0;2
.
Câu 4. Chọn B
Tập xác định
D =
.
2
43y x mx m
= − + +
.
Hàm số đã cho đồng biến trên
2
4 3 0mm
= − −
3
1
4
m −
.
Câu 5. Chọn C
TXĐ
\1
Ta có
( )
2
14
' 0, 1
1
yx
x
= −
−
.
Hàm số nghịch biến trên
( )
;1−
và
( )
1; +
.
Câu 6. Chọn B
Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên khoảng
( )
0;1
.
Câu 7. Chọn D
Dựa vào bảng biến thiên của hàm số ta có hàm số đồng biến trên các khoảng
( )
;2− −
và
( )
0;2
.
Câu 8. Chọn A
Quan sát đồ thị ta thấy :
đồ thị có chiều đi xuống trên khoảng
( )
1;0−
và
( )
1; +
hàm số nghịch biến trên khoảng
( )
1;0−
và
( )
1; +
Vậy chọn Chọn A
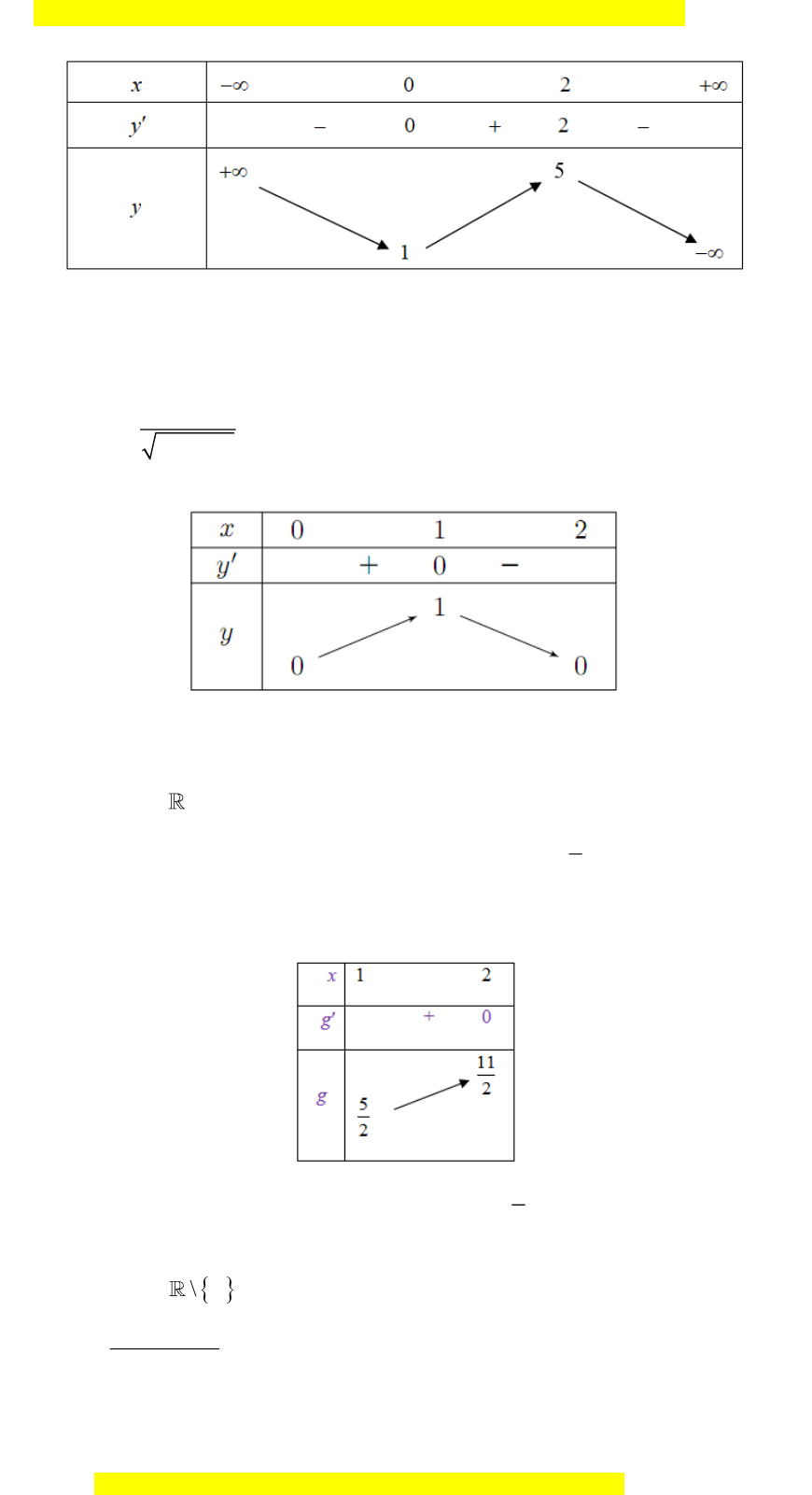
Câu 9. Chọn C
Ta có:
2
36y x x
= − +
.
0y
=
2
3 6 0xx − + =
0
2
x
x
=
=
.
Bảng biến thiên:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng
( )
0;2
.
Câu 10. Chọn B
Tập xác định:
0;2D =
.
Đạo hàm:
( )
2
1
0 2
2
x
yx
xx
−+
=
−+
;
01yx
= =
.
Bảng biến thiên:
.
Từ bảng biến thiên ta thấy hàm số nghịch biến trên khoảng
( )
1;2
.
Câu 11. Chọn D
Tập xác định
D =
. Ta có
3
4 2(2 3)y x m x
= − + −
.
Hàm số nghịch biến trên
(1;2)
2
3
0, (1;2) ( ), (1;2)
2
y x m x g x x
+ =
.
Lập bảng biến thiên của
()gx
trên
(1;2)
.
( ) 2 0 0g x x x
= = =
Bảng biến thiên
Dựa vào bảng biến thiên, kết luận:
5
min ( )
2
m g x m
. Vậy
5 2 7pq+ = + =
.
Câu 12. Chọn A
Tập xác định
\=Dm
.
Ta có:
( )
2
2
6− − +
=
−
mm
y
xm
.
Hàm đồng biến trên
( )
;2− −
( )
2
;2
60
− −
− − +
m
mm
2
2 2.
32
−
−
−
m
m
m
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy có
4
giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 13. Chọn D
Ta có
3
2y x x= + −
2
3 1 0yx
= +
x
. Vậy hàm số đồng biến trên khoảng
( )
;− +
Câu 14. Chọn D
+) Điều kiện
tan xm
. Điều kiện cần để hàm số đồng biến trên
0;
4
là
( )
0;1m
+)
22
2
'
cos (tan )
m
y
x x m
−
=
−
.
+) Ta thấy:
( )
22
1
0 0; ; 0;1
cos (tan ) 4
xm
x x m
−
+) Để hs đồng biến trên
0;
4
' 0 2 0
0
(0;1) 0; 1
ym
m
m m m
− +
hoặc
12m
Câu 15. Chọn C
Ta có
( )
2
2
2015 2016
,
mm
y x m
xm
− + +
= −
+
.
Để hàm số đồng biến trên từng khoảng xác định thì
0,y x m
−
2
2015 2016 0mm − + +
1 2016m −
Mà
m
nên
0;1;...;2015S =
.
Vậy số phần tử của tập
S
là
2016
.
Câu 16. Chọn A
Ta có
2
4y x x m
= − + +
.
Hàm số nghịch biến trên
1;2
0, 1;2yx
2
4 0, 1;2x x m x− + +
2
4 , 1;2m x x x −
( )
2
1;2
min 4m x x −
Xét
( )
2
4g x x x=−
,
( )
2 4 0 2g x x x
= − = =
Dễ thấy
( ) ( )
min 1 ,g 2 4mg = −
.
Vậy không có giá trị nguyên dương nào của
m
thỏa mãn bài toán.
Câu 17. Chọn A
Từ đồ thị ta có hàm số
()y f x=
đồng biến trên mỗi khoảng
( )
;0−
và
( )
2;+
. Hàm số
()y f x=
nghịch biến trên khoảng
( )
0;2
.
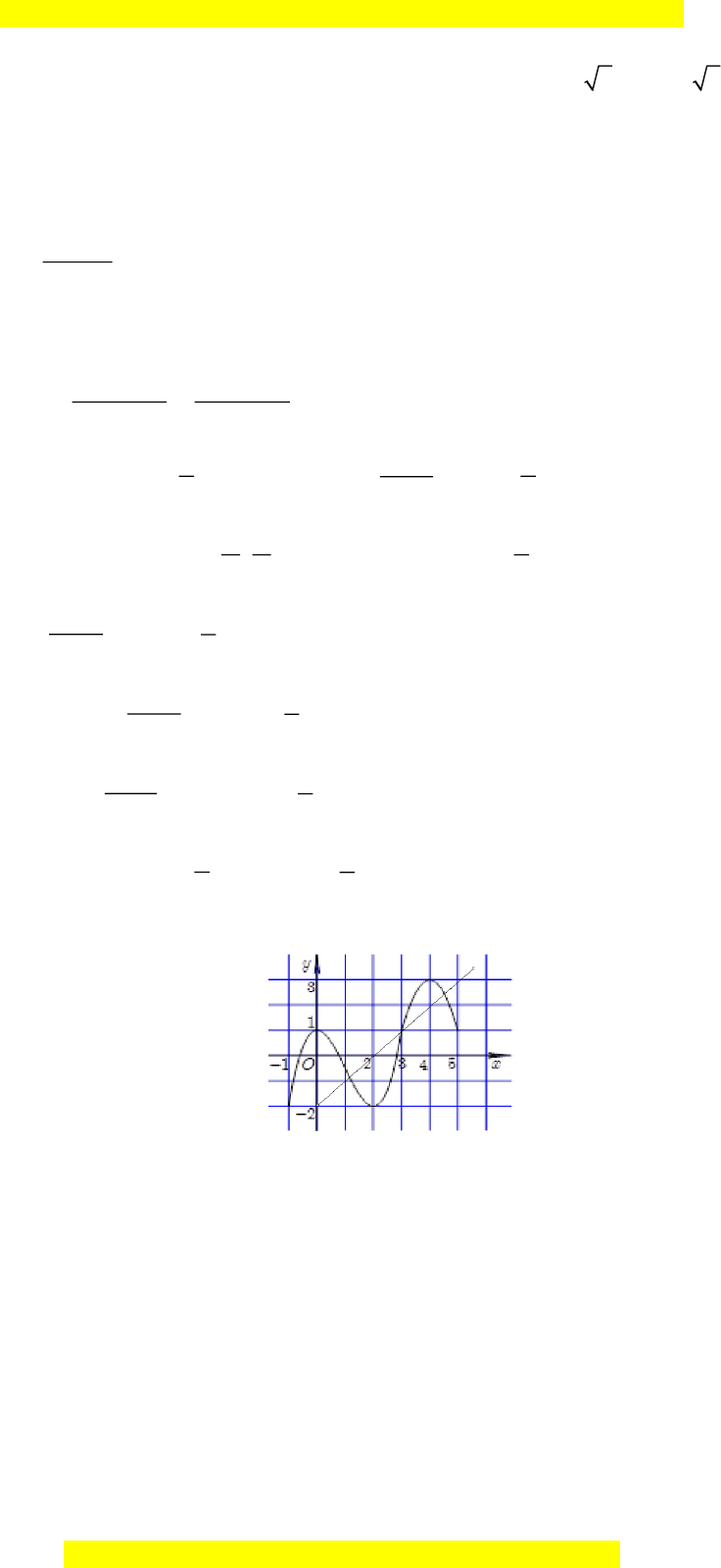
Xét hàm số
2
(2 )y f x=−
ta có
2
2 (2 )y xf x
= − −
.
Để hàm số
2
(2 )y f x=−
đồng biến thì
22
2 (2 ) 0 (2 ) 0xf x xf x
− − −
. Ta có các
trường hợp sau:
TH1:
( )
2
0
20
x
fx
−
2
0
0 2 2
x
x
−
0
2
x
x
02x
.
TH2:
( )
2
0
20
x
fx
−
2
2
0
22
20
x
x
x
−
−
2x
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy hàm số
2
(2 )y f x=−
đồng biến trên các mỗi khoảng
( )
;2− −
và
( )
0; 2
.
Câu 18. ChọnA
3
'( ) 4f x x=
nên hàm số có khoảng đồng biến và nghịch biến.
2
'( ) 8 0g x x=
nên hàm số luôn đồng biến trên R.
2
3
'( ) 0
( 1)
hx
x
=
+
nên hàm số luôn đồng biến trên từng khoảng xác định.
Vậy có 2 hàm số không có khoảng nghịch biến.
Câu 19. Chọn C
Ta có
22
cos cos
sin 1 cos
−−
==
−
m x m x
y
xx
.
Đặt
1
cos , 0;
2
=
t x t
, xét hàm
( )
2
1
−
=
−
mt
gt
t
,
1
0;
2
t
.
Hàm số nghịch biến trên
;
32
khi
( )
1
0, 0;
2
g t t
.
2
1
2
+
t
m
t
,
1
0;
2
t
.
Xét hàm
( )
2
1
2
+
=
t
ht
t
,
1
0;
2
t
.
Ta có
( )
2
2
1
0
2
t
ht
t
−
=
,
1
0;
2
t
.
Lập bảng BBT trên
1
0;
2
, ta có
5
4
m
thỏa YCBT.
Câu 20. Chọn B
Ta có
( )
2
22y f x x= − − +
( ) ( )
2 2 2 2y x f x x
= − − − +
( )
2 2 2y f x x
= − +
( )
0 2 0y f x x
− +
( ) ( )
2 2 2f x x
− − −
.
Dựa vào đồ thị ta thấy đường thẳng
2yx=−
cắt đồ thị
( )
y f x
=
tại hai điểm có hoành
độ nguyên liên tiếp là
1
2
12
3
x
x
=
và cũng từ đồ thị ta thấy
( )
2f x x
−
trên miền
23x
nên
( ) ( )
2 2 2f x x
− − −
trên miền
2 2 3x−
10x −
.
Vậy hàm số nghịch biến trên khoảng
( )
1; 0−
.
Câu 21. Chọn D
Ta có
( )
2
2 2 1 2 8y f x x
= + + −
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Xét
( ) ( )
22
2 2 1 2 8 00 2 1 4f x xy f x x
+ + − +
−
Đặt
21tx=+
, ta có
( )
2
2 15
4
tt
ft
− + +
Vì
2
2 15
0, 3;5
4
tt
t
− + +
−
. Mà
( ) 0, 3;2f t t
−
.
Nên
( )
2
2 15
4
3;2
tt
f t t
− + +
−
.
Suy ra
1
3 2 1 2 2
2
xx− + −
. Vậy chọn phương án D.
Câu 22. Chọn C
TXĐ:
D =
.
Đặt
( )
( )
2 5 3 2 2
11
10 20 1
53
y f x m x mx x m m x= = − + − − − +
.
Ta có
( )
( )
2 4 2 2
20 20f x m x mx x m m
= − + − − −
.
Hàm số đồng biến trên
( )
( )
2 4 2 2
20 20 0,f x m x mx x m m x
= − + − − −
(*).
Ta có
( )
10f
−=
nên
( ) ( )
( )
( )
2 3 2 2 2 2
20 11 ()f x x m m xx m m g xmx m x
− + − +
= + − + = +
. Nếu
1x =−
không phải là nghiệm của
()gx
thì
( )
fx
đổi dấu khi
x
đi qua
1−
, suy ra
( )
fx
không
đồng biến trên .
Do đó điều kiện cần để
( )
0,fx x
là
( )
10g −=
( )
2
2
4 2 20 0 .
5
2
10
m
mm
m
g
=−
− + + =
=
=
−
Với
( ) ( )
( )
32
1 4 4 6 142 f x x x xm x
− +− ++= =
( )
( )
2
2
8 144 01 ,xxxx= − + +
.
và
( )
10fx x= =−
, do đó
()fx
đồng biến trên . Suy ra
2m =−
thoả mãn.
Với
( ) ( )
32
5 25 25 15 65
1
2 4 4 4 4
x x x
m f x x
= = + − + +
( )
( )
2
2
1 25 50 65
0,
4
x x x
x
+ − +
=
và
( )
10fx x= =−
, do đó
()fx
đồng biến
trên . Suy ra
5
2
m =
thoả mãn.
Vậy tổng tất cả các giá trị của tham số
m
là:
51
2.
22
− + =
Câu 23.
Chọn A
Ta có:
( ) ( ) ( ) ( ) ( )( )
32
2 2 2 2 2 2
2 . 9 1y f x x f x x x x x
= = = − −
( )
( ) ( )
22
72
2 9 1 1x x x x= − − +
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
( )
( ) ( )
22
72
0 2 9 1 1 0y x x x x
= − − + =
=
=
=−
=
=−
0 (nghiÖmbéi 7)
3 (nghiÖm ®¬n)
3 (nghiÖm ®¬n)
1 (nghiÖmbéi 2)
1 (nghiÖmbéi 2)
x
x
x
x
x
.
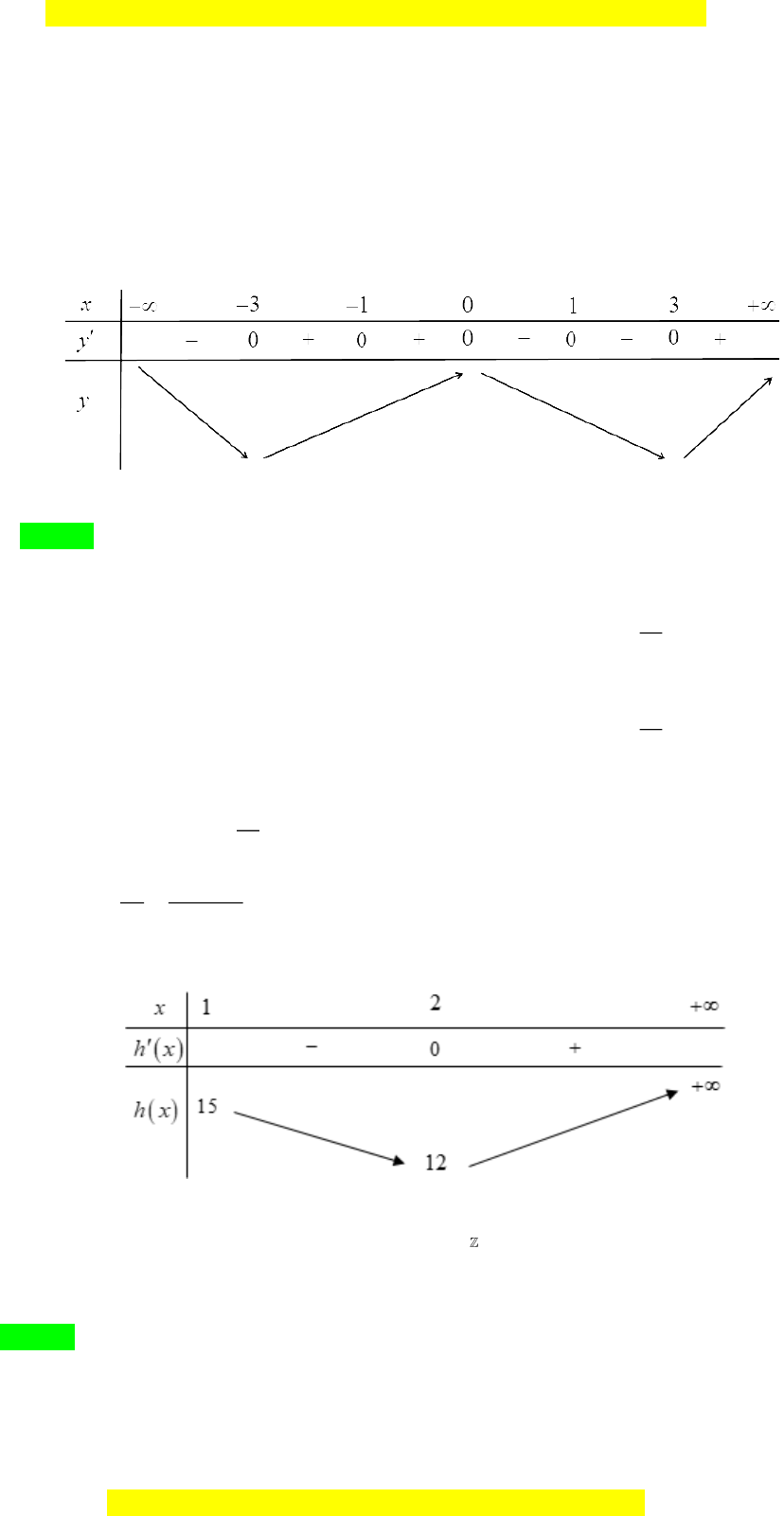
Ta có bảng biến thiên của hàm số
( )
2
y f x=
như sau:
Vậy hàm số
( )
2
y f x=
nghịch biến trên khoảng
( )
;3− −
.
Câu 24. Chọn B
Xét hàm số
( )
32
12 2g x x mx x m= − + +
, ta có
( )
2
3 2 12g x x mx
= − +
YCBT
( ) ( )
( )
( ) ( )
( )
( )
( )
( )
2
2
12
2 3 , 1;
3 2 12 0, 1;
10
13 0
*
12
3 2 12 0, 1;
2 3 , 1;
10
13 0
m x x
g x x mx x
x
g
m
g x x mx x
m x x
x
g
m
+ +
= − + +
+
= − + +
+ +
+
Xét hàm số
( )
12
3h x x
x
=+
trên
( )
1; +
, ta có:
( )
( )
( )
2
2
22
2
12 3 12
3 0 3 12 0
2
x KTM
x
h x x
xx
x TM
=−
−
= − = = − =
=
Bảng biến thiên của
( )
hx
trên
( )
1; +
Từ bảng biến thiên, ta có:
( )
2 12 6
* 13 6 13; 12;...; 1;0;1;2;...;6
13 13
m
mm
mm
mm
− ⎯⎯⎯→ − − −
− −
Vậy có
20
giá trị nguyên của
m
thỏa mãn đề bài.
Câu 25. Chọn C
Ta có :
4 2 2
( ) 4 8 3 ( ) 16 ( 1)f x x x f x x x
= − + = −
Ta có
3
( ) 2 . ( 1).[2 ( 1) . ( 1)]g x x f x f x x f x
= − − + −
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
3
0
( ) 0 ( 1) 0
2 ( 1) . ( 1) 0
x
g x f x
f x x f x
=
= − =
− + − =
(1)
(2)
(3)
Phương trình
(1)
có
0x =
(nghiệm bội ba).
Phương trình
(2)
có cùng số nghiệm với phương trình
( ) 0fx=
nên
(2)
có 4 nghiệm
đơn.
Phương trình
(3)
có cùng số nghiệm với phương trình :
4 2 2
2 ( ) ( 1). ( ) 0 2(4 8 3) 16 ( 1)( 1) 0f x x f x x x x x x
+ + = − + + + − =
4 3 2
24 16 32 16 6 0x x x x + − − + =
có 4 nghiệm phân biệt.
Dễ thấy 9 nghiệm trên phân biệt nên hàm số
( ) 0gx=
có tất cả 9 điểm cực trị.
• Hướng dẫn làm bài vận dụng (Phiếu học tập số 3):
Vận dụng 1. Chọn A
Gọi
t
là số giờ làm tăng thêm (hoặc giảm) mỗi tuần,
t
số công nhân bỏ việc (hoặc tăng thêm) là
2
t
nên số công nhân làm việc là
100
2
t
−
người.
Năng suất của công nhân còn
5
120
2
t
−
sản phẩm một giờ.
Số thời gian làm việc một tuần là
40 t+
giờ.
Để nhà máy hoạt động được thì
40 0
5
120 0
2
100 0
2
t
t
t
+
−
−
( )
40;48t −
.
Số sản phẩm trong một tuần làm được:
( )
5
100 120 40
22
tt
St
= − − +
.
Số sản phẩm thu được là
( ) ( )
( ) ( )
2
95 40 120 40
5
100 120 40
2 2 4
tt
tt
f t t
+ + +
= − − + −
.
( ) ( ) ( ) ( )
1 5 5 5 95
120 40 100 40 100 120 40 30
2 2 2 2 2 2 2
t t t t
f t t t t
= − − + − − + + − − − + −
2
15 1135
2330
42
tt= − −
.
( )
0ft=
( )
4
466
L
3
t
t
=−
=
.
Ta có BBT như sau
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy số lượng sản phẩm thu được mỗi tuần lớn nhất khi
36x =
(giờ).
Vận dụng 2. Chọn D
Cách 1: Anh chèo thuyền của mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
Thời gian chèo thuyền trên quãng đường
AC
:
3
0,5
6
=
(giờ)
Thời gian chạy trên quãng đường
CB
:
8
1
8
=
(giờ)
Tổng thời gian di chuyển từ
A
đến
B
là
1,5
(giờ).
Cách 2: chèo trực tiếp trên quãng đường
22
3 8 73AB = + =
mất
h
73
1 26
6
.
Cách 3:
Gọi
( )
kmx
là độ dài quãng đường
BD
;
( )
8 kmx−
là độ dài quãng đường
CD
.
Thời gian chèo thuyền trên quãng đường
2
9AD x=+
là:
2
9
6
x +
(giờ)
Thời gian chạy trên quãng đường
DB
là:
8
8
x−
(giờ)
Tổng thời gian di chuyển từ
A
đến
B
là
( )
2
98
68
xx
fx
+−
=+
Xét hàm số
( )
2
98
68
xx
fx
+−
=+
trên khoảng
( )
0; 8
Ta có
( )
2
1
8
69
x
fx
x
=−
+
;
( )
2
9
0 3 9 4
7
f x x x x
= + = =
Bảng biến thiên
8 km
3 km
C
D
B
A
8 - x km
x km
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ
A
đến
B
là
h
7
1 1 20
8
+
.
Vậy khoảng thời gian ngắn nhất để người đàn ông đến
B
là
h
7
1 1 20
8
+
.
Ngày ...... tháng ....... năm 2021
BCM ký duyệt
x
0
9
7
8
( )
fx
−
0
+
( )
fx
3
2
73
6
7
1
8
+
Nhắn tin Zalo