15000 câu lý thuyết tách từ đề thi thử Toán tốt nghiệp THPT

Câu 1.
(Cầu Giấy Hà Nội 2023 Lần 1) Nếu hàm số thỏa mãn điều kiện ;
thì số đường tiệm cận ngang của đồ thị hàm số là A. 0. B.1. C. 3. D. 2.
Câu 2. (Chuyên Lê Quý Đôn Quảng Trị Lần 1) Tính số đường tiệm cận của đồ thị hàm số . A. . B. . C. . D. . Câu 3.
(SỞ LÀO CAI 2023) Đồ thị hàm số
có tất cả bao nhiêu đường tiệm cận? A. . B. . C. . D. . Câu 4.
(Lê Xoay lần1)Cho hàm số có và Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
B. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng có phương trình và
C. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng có phương trình và Câu 5.
(Quỳnh Lưu Nghệ An) Cho hàm số
xác định, liên tục trên và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là: A. . B. . C. . D. . Câu 6.
(PHÂN-TÍCH-BL-VÀ-PT-ĐẠI-HỌC-SP-HÀ-NỘI) Nếu hàm số y f
 (x) liên tục trên  thỏa f (x)  f 0 x    1;1 \ 0 mãn       thì
A. Hàm số đạt giá trị nhỏ nhất trên tập số thực tại .
B. Hàm số đạt cực tiểu tại .
C. Hàm số đạt cực đại tại .
D.Hàm số đạt cực tiểu tại . Câu 7. Bất kỳ hàm số xác định trên và thỏa mãn với thì
A. Hàm số đó đạt cực tiểu tại .
B.Hàm số đó đạt cực đại tại .
C. Hàm số đó đạt cực tiểu tại .
D. Hàm số đó đạt cực đại tại .

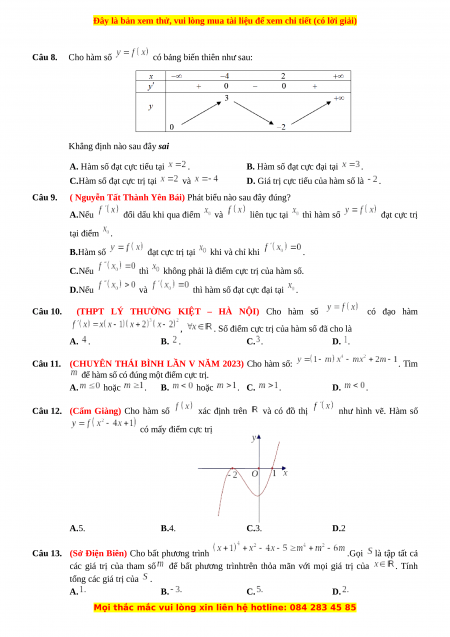
Câu 8. Cho hàm số
có bảng biến thiên như sau:
Khẳng định nào sau đây sai
A. Hàm số đạt cực tiểu tại .
B. Hàm số đạt cực đại tại .
C.Hàm số đạt cực trị tại và
D. Giá trị cực tiểu của hàm số là . Câu 9.
( Nguyễn Tất Thành Yên Bái) Phát biểu nào sau đây đúng? A.Nếu
đổi dấu khi qua điểm và
liên tục tại thì hàm số đạt cực trị tại điểm . B.Hàm số đạt cực trị tại khi và chỉ khi . C.Nếu thì
không phải là điểm cực trị của hàm số. D.Nếu và
thì hàm số đạt cực đại tại .
Câu 10. (THPT LÝ THƯỜNG KIỆT – HÀ NỘI) Cho hàm số có đạo hàm ,
. Số điểm cực trị của hàm số đã cho là A. . B. . C. . D. .
Câu 11. (CHUYÊN THÁI BÌNH LẦN V NĂM 2023) Cho hàm số: . Tìm
để hàm số có đúng một điểm cực trị. A. hoặc . B. hoặc . C. . D. .
Câu 12. (Cẩm Giàng) Cho hàm số
xác định trên và có đồ thị như hình vẽ. Hàm số có mấy điểm cực trị A.5. B.4. C.3. D.2
Câu 13. (Sở Điện Biên) Cho bất phương trình .Gọi là tập tất cả
các giá trị của tham số để bất phương trìnhtrên thỏa mãn với mọi giá trị của . Tính tổng các giá trị của . A. B. C. D.


Câu 14. (Đặng Thành Nam Đề 17) Có bao nhiêu số nguyên để hàm số
đạt giá trị nhỏ nhất tại điểm A. Vô số. B. . C. . D. .
Câu 15. (Chuyên Lê Hồng Phong Nam Định Lần 1) Gọi là tập hợp các giá trị nguyên để đồ thị hàm số
có điểm cực trị. Tính tổng các phần tử của . A. . B. . C. . D. .
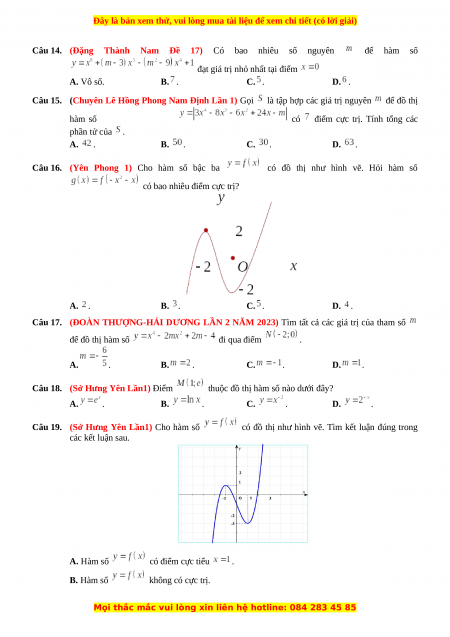
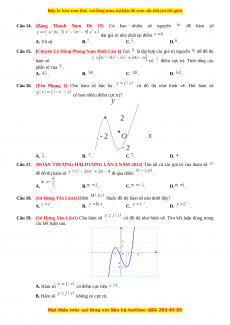
Câu 16. (Yên Phong 1) Cho hàm số bậc ba
có đồ thị như hình vẽ. Hỏi hàm số
có bao nhiêu điểm cực trị? A. . B. . C. . D. .
Câu 17. (ĐOÀN THƯỢNG-HẢI DƯƠNG LẦN 2 NĂM 2023) Tìm tất cả các giá trị của tham số để đồ thị hàm số đi qua điểm . A. . B. . C. . D. .
Câu 18. (Sở Hưng Yên Lần1) Điểm
thuộc đồ thị hàm số nào dưới đây? A. . B. . C. . D. .
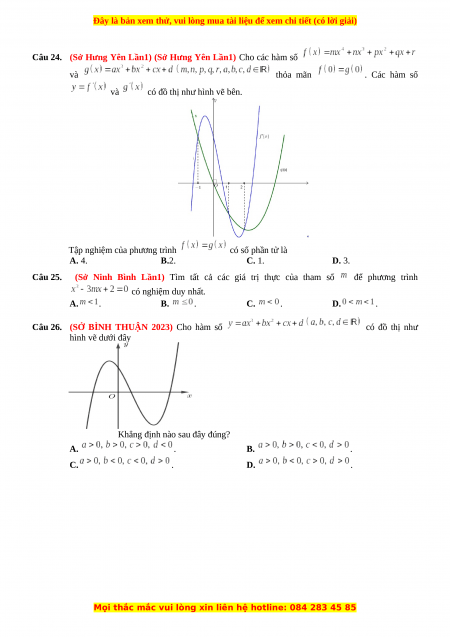
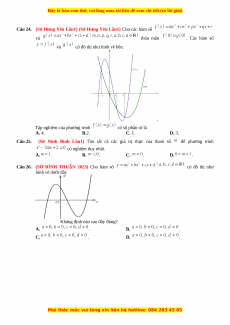
Câu 19. (Sở Hưng Yên Lần1) Cho hàm số
có đồ thị như hình vẽ. Tìm kết luận đúng trong các kết luận sau. A. Hàm số có điểm cực tiểu . B. Hàm số không có cực trị.

C. Phương trình vô nghiệm. D. Hàm số
đồng biến trên khoảng .
Câu 20. (Hậu Lộc Thanh Hóa) Cho hàm số
xác định và liên tục trên và có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị cực tiểu bằng hoặc .
B. Hàm số có giá trị lớn nhất bằng và giá trị nhỏ nhất bằng .
C. Đồ thị hàm số có đúng điểm cực trị.
D.Hàm số đạt cực đại tại .
Câu 21. (Chuyên-Thái-Nguyên-lần-1-2022-2023-Thi-tháng-3)Cho hàm số xác định, liên
tục trên và có bảng biến thiên:
Mệnh đề nào sau đây đúng?
A.Hàm số đạt cực đại tại
và đạt cực tiểu tại .
B. Hàm số có giá trị lớn nhất bằng và giá trị nhỏ nhất bằng .
C. Hàm số có đúng một cực trị.
D. Hàm số có giá trị cực đại bằng .
Câu 22. (HKII-CHUYÊN-NGUYỄN-HUỆ-HÀ-NỘI) Cho hàm số xác định trên ,
liên tục trên mỗi khoảng xác định và có bảng biến thiên sau
Hỏi khẳng định nào dưới đây là khẳng định sai?
A.Đồ thị hàm số có hai tiệm cận đứng là các đường thẳng và .
B.Hàm số không có đạo hàm tại điểm .
C.Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng và .
D.Hàm số đạt cực trị tại điểm .
Câu 23. (Chuyên Ngoại Ngữ Hà Nội) Cho hàm số liên tục trên đoạn và
, khẳng định nào sau đây sai? A. . B. . C. đồng biến trên . D.