Bộ tài liệu, chuyên đề ôn thi Toán tốt nghiệp THPT điểm 8,9,10

CHƯƠNG 1: MỆNH ĐỀ, TẬP HỢP, HÀM SỐ
CHUYÊN ĐỀ 1: MỆNH ĐỀ, TẬP HỢP
PHẦN 1: LÝ THUYẾT TRỌNG TÂM 1. Mệnh đề Định nghĩa:
• Mệnh đề là một câu khẳng định đúng hoặc một câu khẳng định sai.
• Một mệnh đề không thể vừa đúng, vừa sai. Mệnh đề phủ định
Cho mệnh đề P, mệnh đề “không phải P” được gọi là mệnh đề phủ định của P và kí hiệu là Nếu P
đúng thì sai, nếu P sai thì đúng. Mệnh đề kéo theo
Cho mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo và kí hiệu là , (P suy ra Q). Mệnh đề
chỉ sai khi P đúng và Q sai. Chú ý:
Các định lí toán học thường có dạng . Khi đó:
P là giả thiết, Q là kết luận, P là điều kiện đủ để có Q, Q là điều kiện cần để có P. Mệnh đề đảo
• Cho mệnh đề kéo theo . Mệnh đề
được gọi là mệnh đề đảo của mệnh đề .
• Cho mệnh đề P và Q. Mệnh đề “P nếu và chỉ nếu Q” được gọi là mệnh đề tương đương và kí hiệu là . Mệnh đề
đúng khi và chỉ khi cả hai mệnh đề và đều đúng. Chú ý: Nếu mệnh đề
là 1 định lí thì ta nói P là điều kiện cần và đủ để có Q. Kí hiệu và :
Cho mệnh đề chứa biến P (x). Khi đó:
“Với mọi x thuộc X để P (x) đúng” được ký hiệu là: “ ” hoặc “ ”.
“Tồn tại x thuộc X để P (x) đúng” được ký hiệu là “ ” hoặc “ ”
• Mệnh đề phủ định của mệnh đề “ ” là “ ”.
• Mệnh đề phủ định của mệnh đề “ ” là “ ”. 2. Tập hợp
Tập hợp là một khái niệm cơ bản của toán học, không định nghĩa. Các xác định tập hợp
Liệt kê các phân từ: Viết các phần tử của tập hợp trong hai dấu móc { ; ; }.
Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Tập rỗng: là tập hợp không chứa phần tử nào, kí hiệu . Trang 1

Tập hợp con: . Tập hợp bằng nhau: Chú ý:
Nếu tập hợp có n phần tử thì có 2n tập con.
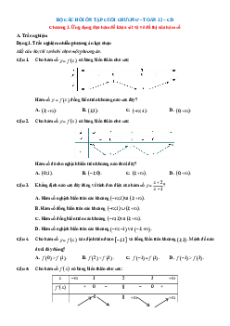
3. Một số tập hợp con của tập hợp số thực
là tập hợp số tự nhiên không có số 0.
là tập hợp số tự nhiên. là tập hợp số nguyên.
là tập hợp số hữu tỉ. là tập hợp số thực. Khoảng Đoạn: Nửa khoảng:
4. Các phép toán trên tập hợp Giao của hai tập hợp { và }. Hợp của hai tập hợp { hoặc }. Hiệu của hai tập hợp: { và }. Phần bù: Cho thì 5. Số gần đúng Sai số tuyệt đối
Nếu a là số gần đúng của số đúng thì
gọi là sai số tuyệt đối của số gần đúng a.
Độ chính xác của một số gần đúng Trang 2

Nếu thì
. Ta nói a là số gần đúng của với độ chính xác d và qui ước viết gọn là Sai số tương đối
Sai số tương đối của số gần đúng a là tỉ số giữa sai số tuyệt đối và kí hiệu càng
nhỏ thì độ chính xác của phép đo đạc hoặc tính toán càng lớn.
Ta thường viết dưới dạng phần trăm. Quy tròn số gần đúng
Nếu chữ số ngay sau hàng qui tròn nhỏ hơn 5 thì ta chỉ việc thay thế chữ số đó và các chữ số bên phải nó bởi số 0.
Nếu chữ số ngay sau hàng qui tròn lớn hơn hay bằng 5 thì ta thay thế chữ số đó và các chữ số bên
phải nó bởi số 0 và cộng thêm một đơn vị vào chữ số ở hàng qui tròn. Chữ số chắc
Cho số gần đúng a của số với độ chính xác d. Trong số a, một chữ số gọi là chữ số chắc (hay
đáng tin) nếu d không vượt quá nửa đơn vị của hàng có chữ số đó.
Nhận xét: Tất cả các chữ số đứng bên trái chữ số chắc đều là chữ số chắc. Tất cả các chữ số đứng bên
phải chữ số không chắc đều là chữ số không chắc.
PHẦN 2: CÁC DẠNG BÀI TẬP Dạng 1: Mệnh đề 1. Ví dụ minh họa
Ví dụ 1: Các câu sau đây, có bao nhiêu câu là mệnh đề đúng? (1) Chạy ngay đi! (2) Phương trình vô nghiệm.
(3) 16 không là số nguyên tố. (4) Hai phương trình và có nghiệm chung.
(5) Ba giờ sáng anh còn chưa ngủ, tương tư về em biết bao nhiêu cho đủ?
(6) U23 Việt Nam đoạt giải chơi đẹp nhất U23 Châu Á.
(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau. A. 4. B. 6. C. 7. D. 5. Hướng dẫn
Câu (1) và (5) không là mệnh đề (vì là câu đầu khiến, câu nghi vấn).
Các câu (3), (4), (6), (8) là những mệnh đề đúng.
Câu (2) và (7) là những mệnh đề sai. Chọn A. Trang 3


Ví dụ 2: Mệnh đề
. Phủ định của mệnh đề P là A. B. C. D. Hướng dẫn
Phủ định của mệnh đề P là Chọn D.
Ví dụ 3: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều di chuyển”?
A. Mọi động vật đều không di chuyển.
B. Mọi động vật đều đứng yên.
C. Có ít nhất một động vật không di chuyển.
D. Có ít nhất một động vật di chuyển. Hướng dẫn
Phủ định của mệnh đề là mệnh đề
Do đó, phủ định của mệnh đề: “Mọi động vật đều di chuyển” là mệnh đề: “Có ít nhất một động vật không di chuyển”. Chọn C. 2. Bài tập tự luyện
Câu 1. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
Câu 2. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. “ABC là tam giác đều khi và chỉ khi tam giác ABC cân”.
B. “ABC là tam giác đều khi và chỉ khi tam giác ABC cân và có một góc ”.
C. “ABC là tam giác đều khi và chỉ khi ABC là tam giác có ba cạnh bằng nhau”.
D. “ABC là tam giác đều khi và chỉ khi tam giác ABC có hai góc bằng ”.
Câu 3. Cho mệnh đề
Mệnh đề phủ định của mệnh đề P (x) là A. B. C. D.
Câu 4. Lập mệnh đề phủ định của mệnh đề: “Số 6 chia hết cho 2 và 3”.
A. Số 6 chia hết cho 2 hoặc 3.
B. Số 6 không chia hết cho 2 và 3.
C. Số 6 không chia hết cho 2 hoặc 3.
D. Số 6 không chia hết cho 2, chia hết cho 3. Trang 4