Phân dạng 32 chủ đề quan trọng luyện thi Toán tốt nghiệp THPT năm 2023

CHỦ ĐỀ 1
A. KIẾN THỨC NỀN TẢNG 1. Khái niệm
Giá trị lớn nhất của hàm số
trên miền D là M nếu với ọi giá trị thì .
Giá trị nhỏ nhất của hàm số
trên miền D là m nếu với mọi giá thì .
Quy ước: GTLN, GTNN là viết tắt của giá trị lớn nhất và giá trị nhỏ nhất.
2. Quy tắc tìm GTLN, GTNN
Bước 1: Tìm các giá trị tới hạn trên miền D (là các giá trị làm cho và các cận của D)
Bước 2: Tính giá trị của
tại các điểm tới hạn.
Bước 3: So sánh các giá trị này để tìm GTLN, GTNN.
3. Tìm GTLN, GTNN bằng máy tính Casio
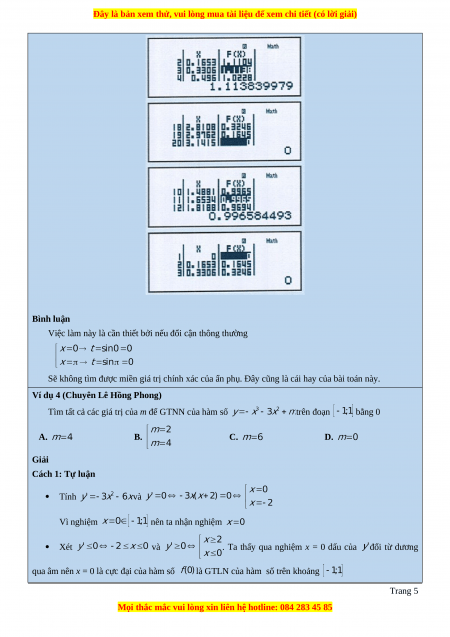
Sử dụng chức năng MODE 7 với thiết lập Start a End b và với Quan sát bảng giá trị
để tìm GTLN, GTNN xuất hiện trên màn hình máy tính. B. VÍ DỤ MINH HỌA
Ví dụ 1 (Chuyên HN Amsterdam):
Gọi các giá trị lớn nhất và giá trị nhỏ nhất trên đoạn
lần lượt tại M và m. Khi đó
giá trị M.m là: A. -2 B. 46 C. -23 D. 48 Giải Cách 1: Tự luận Tính và Vì nghiệm nên nghiệm 0 nhận. Tính , , Ta có: và
Vậy M.m = –23 => Chọn C Cách 2: Casio và Vinacal 
Sử dụng tính năng MODE 7 cho hàm số
với thiết lập Start -1 End 2 và
Quan sát bảng giá trị ta thấy GTLN là 23 đạt được khi và đạt được khi . Vậy Trang 1

=> Chọn C Phân tích
2 cách trên đều rất tuyệt vời. Khi học ở nhà thì nên chọn cách 1 để rèn luyện kiến thức nhưng khi đi
thi thì nên chọn cách số 2 để tính nhanh.
Ví dụ 2 (Chuyên Khoa học tự nhiên HN) Hàm số có tập giá trị là: A. B. C. D. Giải Cách 1: Tự luận  Tìm tập xác định: Tính và Vì nghiệm nên cả 2 nghiệm đều nhận. Tính , , , Ta có: và Vậy => Tập giá trị của là => Chọn D Cách 2: Casio và Vinacal 
Sử dụng tính năng MODE 7 cho hàm số
với thiết lập Start –1 End 1 Trang 2


Quan sát bảng giá trị ta thấy GTLN là đạt được khi và đạt được khi . Vậy => Chọn D Phân tích
Tập giá trị của hàm số thường được kí hiệu là chữ P là tập hợp tất cả các giá trị của y khi x thay đổi. Vậy Bình luận
Việ tìm được điều kiện của
là điều rất quan trọng trong bài toán tìm GTLN, GTNN
Ví dụ 3 (Chuyên Sư phạm HN) Tìm GTLN của hàm số trên A. B. C. D. Giải Cách 1: Tự luận
Việc tính đạo hàm và xét dấu đạo hàm của hàm lượng giác
là việc làm khó khăn. Vì vậy
để đợn giản ta tiến hành đặt ẩn phụ. Đặt , khi đó . Tiến hành đổi cận  Thay vào hàm ta được: trên miền . Tính và Vì nghiệm
nên nghiệm này thỏa mãn. , , Trang 3


Vậy GTLN của f đạt được là và dấu = xảy ra khi => Chọn D Cách 2: Casio và Vinacal
Sử dụng tính năng MODE 7 cho hàm
với thiết lập Start 0 End
Quan sát bảng giá trị ta thấy GTLN là đạt được khi => Chọn D Phân tích
Khi tìm GTLN, GTNN của hàm lượng giác ta phải chuyển máy tính về chế độ Radian
Khi tiến hành đổi biến ta phải đổi cả miền giá trị của biến bằng cách khảo sát hàm với chức năng MODE 7 Ta thấy rõ ràng
có giá trị xuất phát từ 0 tăng lên 1 rồi lại giảm về 0 Trang 4