TRƯỜNG HOÀI ĐỨC A – HÀ NỘI
THI THỬ TỐT NGHIỆP THPT NĂM HỌC - 2022-2023 ĐỀ 02 Câu 1:
Hàm số nào trong bốn hàm số liệt kê ở dưới nghịch biến trên từng khoảng xác định của nó? A. . B. . C. . D. . Câu 2: Hàm số
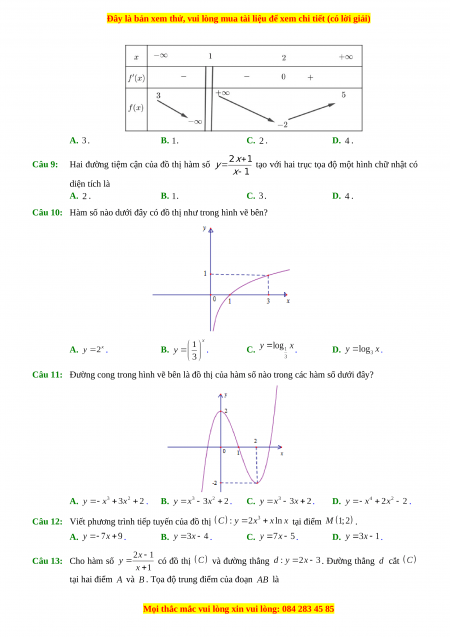
đồng biến trên khoảng nào sau đây? A. . B. . C. . D. . Câu 3: Cho hàm số liên tục trên
và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại điểm .
B. Hàm số có giá trị nhỏ nhất trên bằng
C. Hàm số có giá trị cực đại bằng
D. Hàm số chỉ có một điểm cực trị. Câu 4: Hàm số
có mấy điểm cực trị? A. . B. . C. . D. . Câu 5: Hàm số
nghịch biến trên khoảng nào sau đây? A. . B. . C. . D. . Câu 6: Gọi
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn . Tổng bằng A. . B. . C. . D. . Câu 7:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn là A. . B. . C. . D. . Câu 8: Cho hàm số
có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả
bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. . B. . C. . D. . Câu 9:
Hai đường tiệm cận của đồ thị hàm số
tạo với hai trục tọa độ một hình chữ nhật có diện tích là A. . B. . C. . D. .
Câu 10: Hàm số nào dưới đây có đồ thị như trong hình vẽ bên? A. . B. . C. . D. .
Câu 11: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây? A. . B. . C. . D. .
Câu 12: Viết phương trình tiếp tuyến của đồ thị tại điểm . A. . B. . C. . D. . Câu 13: Cho hàm số có đồ thị và đường thẳng . Đường thẳng cắt
tại hai điểm và . Tọa độ trung điểm của đoạn là
A. . B. . C. . D. . Câu 14: Cho hàm số (với là tham số thực, ). Hàm số
có bao nhiêu điểm cực trị? A. . B. . C. . D. . Câu 15: Cho hàm số
có đạo hàm liên tục trên
và có đồ thị hàm số như hình vẽ sau. Gọi . Biết . Với thì
đạt giá trị nhỏ nhất bằng A. . B. . C. . D. .
Câu 16: Rút gọn biểu thức với
. Khẳng định nào sau đây đúng? A. . B. . C. . D. .
Câu 17: Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của ? A. . B. . C. . D. .
Câu 18: Cho số thực dương với
. Tìm mệnh đề dúng trong các mệnh đề dưới đây. A. . B. . C. . D. .
Câu 19: Hãy cho biết giá trị của nếu . A. . B. . C. . D. .
Câu 20: Đạo hàm của hàm số là nào số nào sau đây? A. . B. . C. . D. .
Câu 21: Cho hai số và với
. Khẳng định nào dưới đây là khẳng định đúng?
A. . B. . C. . D. .
Câu 22: Tìm tất cả các giá trị thực của tham số để hàm số đồng biến trên khoảng ? A. . B. . C. . D. . Câu 23: Cho hàm số . Biết rằng với
là các số nguyên dương nguyên tố cùng nhau. Tính . A. . B. . C. . D. .
Câu 24: Số nghiệm của phương trình là A. . B. . C. . D. .
Câu 25: Phương trình có hai nghiệm . Giá trị bằng A. . B. . C. . D. .
Câu 26: Tập nghiệm của phương trình là A. . B. . C. . D. .
Câu 27: Giải phương trình
. Ta có tổng các nghiệm là A. . B. . C. . D. .
Câu 28: Tập nghiệm của bất phương trình A. . B. . C. D. .
Câu 29: Tập nghiệm của bất phương trình có dạng trong đó là các số
nguyên. Giá trị biểu thức bằng A. . B. . C. . D. .
Câu 30: Tập nghiệm của bất phương trình là: A. . B. . C. . D. .
Câu 31: Bất phương trình
nghiệm đúng với mọi số thực khi A. . B. . C. . D. .
Đề thi thử Toán trường Hoài Đức A - Hà Nội - Đề 2 năm 2023
539
270 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Đề thi thử THPT Quốc Gia Toán trường THPT Hoài Đức A - Hà Nội - Đề 2 bản word có lời giải chi tiết.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(539 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Tốt nghiệp THPT
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
TRƯỜNG HOÀI ĐỨC A – HÀ NỘI
THI THỬ TỐT NGHIỆP THPT NĂM HỌC - 2022-2023
ĐỀ 02
Câu 1: Hàm số nào trong bốn hàm số liệt kê ở dưới nghịch biến trên từng khoảng xác định của nó?
A. . B. . C. . D. .
Câu 2: Hàm số đồng biến trên khoảng nào sau đây?
A. . B. . C. . D. .
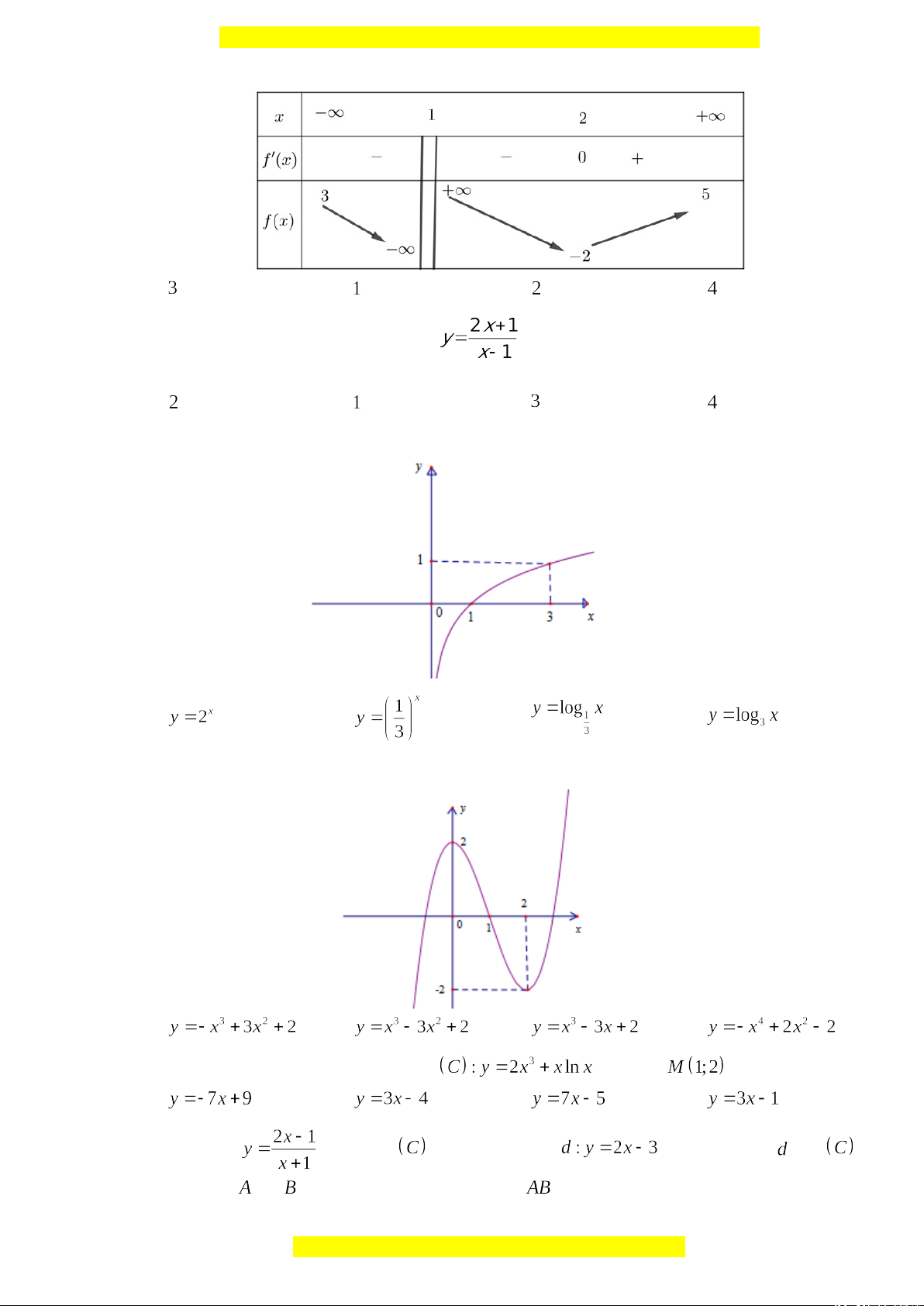
Câu 3: Cho hàm số liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại điểm . B. Hàm số có giá trị nhỏ nhất trên bằng
C. Hàm số có giá trị cực đại bằng D. Hàm số chỉ có một điểm cực trị.
Câu 4: Hàm số có mấy điểm cực trị?
A. . B. . C. . D. .
Câu 5: Hàm số nghịch biến trên khoảng nào sau đây?
A. . B. . C. . D. .
Câu 6: Gọi lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên
đoạn . Tổng bằng
A. . B. . C. . D. .
Câu 7: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn là
A. . B. .
C. . D. .
Câu 8: Cho hàm số có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả
bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Mọi thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
A. . B. . C. . D. .
Câu 9: Hai đường tiệm cận của đồ thị hàm số tạo với hai trục tọa độ một hình chữ nhật có
diện tích là
A. . B. . C. . D. .
Câu 10: Hàm số nào dưới đây có đồ thị như trong hình vẽ bên?
A. . B. . C. . D. .
Câu 11: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?
A. . B. . C. . D. .
Câu 12: Viết phương trình tiếp tuyến của đồ thị tại điểm .
A. . B. . C. . D. .
Câu 13: Cho hàm số có đồ thị và đường thẳng . Đường thẳng cắt
tại hai điểm và . Tọa độ trung điểm của đoạn là
Mọi thắc mắc vui lòng xin vui lòng: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
A. . B. . C. . D. .
Câu 14: Cho hàm số (với là tham số thực, ). Hàm số
có bao nhiêu điểm cực trị?
A. . B. . C. . D. .
Câu 15: Cho hàm số có đạo hàm liên tục trên và có đồ thị hàm số như hình vẽ
sau.
Gọi . Biết . Với thì
đạt giá trị nhỏ nhất bằng
A. . B. . C. . D. .
Câu 16: Rút gọn biểu thức với . Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 17: Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của ?
A. . B. . C. . D. .
Câu 18: Cho số thực dương với . Tìm mệnh đề dúng trong các mệnh đề dưới đây.
A. . B. .
C. . D. .
Câu 19: Hãy cho biết giá trị của nếu .
A. . B. . C. . D. .
Câu 20: Đạo hàm của hàm số là nào số nào sau đây?
A. . B. . C. . D. .
Câu 21: Cho hai số và với . Khẳng định nào dưới đây là khẳng định đúng?
Mọi thắc mắc vui lòng xin vui lòng: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
A. . B. .
C. . D. .
Câu 22: Tìm tất cả các giá trị thực của tham số để hàm số đồng biến trên khoảng
?
A. . B. . C. . D. .
Câu 23: Cho hàm số . Biết rằng với
là các số nguyên dương nguyên tố cùng nhau. Tính .
A. . B. . C. . D. .
Câu 24: Số nghiệm của phương trình là
A. . B. . C. . D. .
Câu 25: Phương trình có hai nghiệm . Giá trị bằng
A. . B. . C. . D. .
Câu 26: Tập nghiệm của phương trình là
A. . B. . C. . D. .
Câu 27: Giải phương trình . Ta có tổng các nghiệm là
A. . B. . C. . D. .
Câu 28: Tập nghiệm của bất phương trình
A.
.
B. . C. D.
.
Câu 29: Tập nghiệm của bất phương trình có dạng
trong đó là các số
nguyên. Giá trị biểu thức bằng
A.
.
B. . C.
.
D.
.
Câu 30: Tập nghiệm của bất phương trình là:
A.
.
B. . C.
.
D.
.
Câu 31: Bất phương trình nghiệm đúng với mọi số thực khi
A. . B. . C. . D. .
Mọi thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Câu 32: Tìm số nghiệm nguyên của bất phương trình
A. 6. B. 5. C. 4. D. 3.
Câu 33: Hình bát diện đều có bao nhiêu cạnh?
A. . B. . C. . D. .
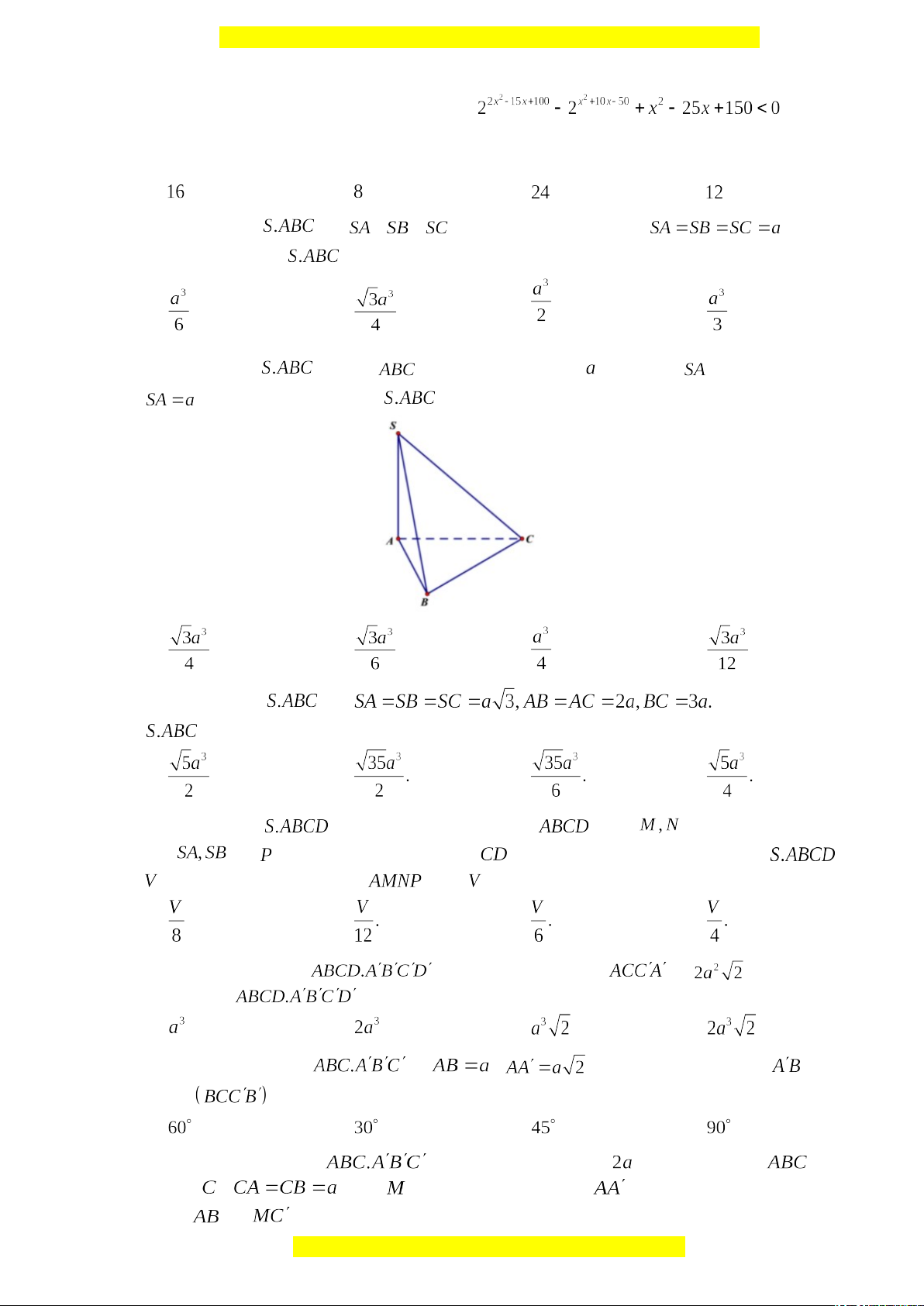
Câu 34: Cho hình chóp có , , đôi một vuông góc. Biết . Tính thể
tích của khối chóp
A. . B. . C. . D. .
Câu 35: Cho hình chóp có đáy là tam giác đều cạnh , cạnh bên vuông góc với đáy,
. Thể tích của khối chóp bằng:
A. . B. . C. . D. .
Câu 36: Cho hình chóp có Thể tích của khối
bằng
A. . B. C. D.
Câu 37: Cho hình chóp có đáy là hình bình hành . Gọi lần lượt là trung điểm
của và là điểm bất kì thuộc cạnh . Biết rằng thể tích của khối chóp là
. Tính thể tích khối tứ diện theo .
A. . B. C. D.
Câu 38: Cho hình lập phương có diện tích mặt chéo là . Thể tích khối
lập phương là:.
A. . B. . C. . D. .
Câu 39: Cho khối lăng trụ đều có , . Góc giữa đường thẳng và mặt
phẳng bằng
A. . B. . C. . D. .
Câu 40: Cho khối lăng trụ đứng có độ dài cạnh bên bằng , đáy là tam giác vuông
cân tại ; . Gọi là trung điểm của cạnh . Khoảng cách giữa hai đường
thẳng
và bằng
Mọi thắc mắc vui lòng xin vui lòng: 084 283 45 85