Đề thi thử tốt nghiệp THPT 2026 Toán (từ Trường/Sở)

SỞ GD&ĐT BẮC NINH
ĐỀ KSCL ÔN THI TN THPT 2026
TRƯỜNG THPT CHUYÊN BẮC NINH MÔN THI: TOÁN 12
Thời gian: 90 phút (Không kể thời gian phát đề) 2025-2026
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án Câu 1. Cho hàm số 2x 1 y 
. Giá trị f 3 bằng x 1 A. 4 . B. 3 . C. 2 . D. 1 . 5 16 9 6 
Câu 2. Cho hình lập phương ABC . D AB C  D
  . Vectơ nào dưới đây bằng vectơ AD ?     A. BC . B. DC . C. B C  . D. AB . 1
Câu 3. Tập xác định của hàm số y  x     2 6 1 log 4  x  là A. 1;2 . B. 2;2 . C. 1;2. D. 1;2 .
Câu 4. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm như sau:
Trung vị của mẫu số liệu trên gần với số nào nhất? A. 41,23 . B. 51,54. C. 40,55. D. 50,44 . Câu 5. Cho hàm số 3 2
y  x  3x  9x 1. Hệ số góc lớn nhất của tiếp tuyến với đồ thị hàm số là A. 9. B. 12. C. 6. D. 8.
Câu 6. Giá trị của giới hạn 3 3 2
lim n 2n  n bằng A. 1 . B. 2  . C. 1. D. 0. 3 3
Câu 7. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O ,O 1 2
lần lượt là tâm của ABCD , ABEF . M là trung điểm của CD . Chọn khẳng định sai trong các khẳng định sau
A. MO cắt BEC .
B. O O song song với  AFD. 2 1 2
C. O O song song với BEC .
D. O O song song với EFM  . 1 2 1 2
Câu 8. Tập giá trị của hàm số y  cotx là A. 1;  1 . B. 1;  1 . C. . D.  ;  0 .
Câu 9. Cho tứ diện ABCD . Gọi G là trọng tâm tam giác ABC . Phát biểu nào sau đây là sai?
      
A. DA  DB  DC  3DG .
B. GD GA  AD .
   
    
C. GA GB  GC  0.
D. GA GB  GC  GD  0.
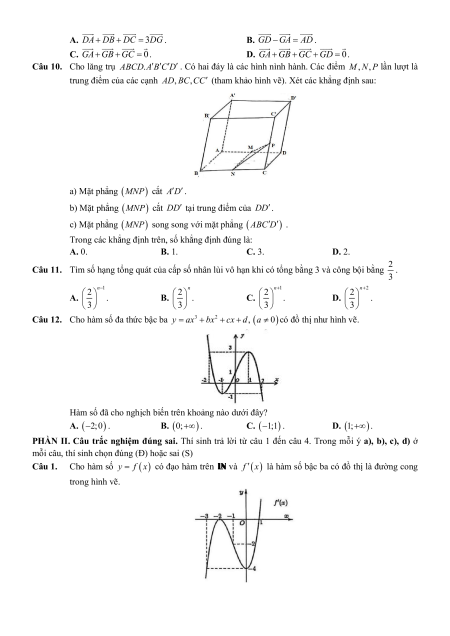
Câu 10. Cho lăng trụ ABC . D AB C  D
  . Có hai đáy là các hình nình hành. Các điểm M , N, P lần lượt là
trung điểm của các cạnh AD, BC,CC (tham khảo hình vẽ). Xét các khẳng định sau:
a) Mặt phẳng MNP cắt AD.
b) Mặt phẳng MNP cắt DD tại trung điểm của DD.
c) Mặt phẳng MNP song song với mặt phẳng  ABC D   .
Trong các khẳng định trên, số khẳng định đúng là: A. 0. B. 1. C. 3. D. 2.
Câu 11. Tìm số hạng tổng quát của cấp số nhân lùi vô hạn khi có tổng bằng 3 và công bội bằng 2 . 3 n 1  n n 1  n2 A.  2     2   2   . B. 2 . C. . D. . 3           3   3   3 
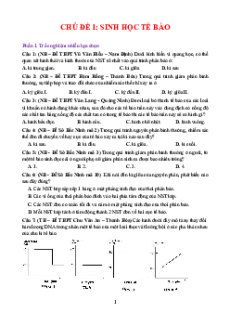
Câu 12. Cho hàm số đa thức bậc ba 3 2
y  ax  bx  cx  d, a  0có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 2;0 . B. 0; . C. 1;  1 . D. 1;.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
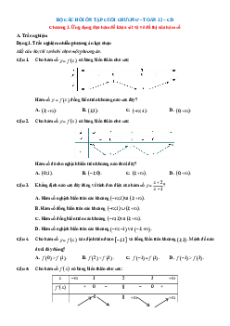
Câu 1. Cho hàm số y  f  x có đạo hàm trên  và f x là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.
a) Đồ thị hàm số g x  f x 1 2
 x  x  2025 cắt đường thẳng y  m tại bốn điểm phân biệt 2
khi và chỉ khi g  
1  m  ming 3; g   1 .
b) Đồ thị hàm số 
hx 2x 1  có 3 đường tiệm cận. f x
c) Hàm số y  f  x đồng biến trên khoảng 0;.
d) Hàm số y  f  x có hai điểm cực trị.
Câu 2. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng 2a . Gọi F là trung
điểm của cạnh SA .
a) Khoảng cách từ S đến mặt phẳng FCD bằng a 10 . 5
b) Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng 30 . 3
c) Thể tích của khối chóp S.FCD bằng a 3 . 24
d) Khoảng cách giữa AC và SB bằng a 6 . 4
Câu 3. Trong hộp có 45 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 45. Lấy ngẫu
nhiên 3 quả cầu từ hộp đó.
a) Số cách lấy được cả 3 quả cầu đánh số chẵn bằng 1540.
b) Xác xuất để tích 3 số ghi trên 3 quả cầu là một số chia hết cho 8 bằng 523 . 1290
c) Xác xuất để tổng 3 số ghi trên 3 quả cầu là số lẻ bằng 1 . 2
d) Xác xuất để tổng 3 số ghi trên 3 quả cầu là số chia hết cho 4 bằng 323 . 1290 1
Câu 4. Cho hàm số y   2  x 3 9  ln 1 x .
a) Tập xác định của hàm số là khoảng  ;   1 .
b) Hàm số có đạo hàm 1 1 y   .   2 2 3 1 3 9  x x
c) Hàm số nghịch biến trên khoảng 0;  1 .
d) Giá trị nhỏ nhất của hàm số trên đoạn 1 1 ;  1  bằng 3 70  ln 2 . 4 2   2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.          
Câu 1. Cho hai vectơ a , b sao cho a  2 , b  2 và hai vectơ x  a  b , y  2a  b vuông góc với  
nhau. Tính góc giữa hai vectơ a và b (đơn vị độ). 2
Câu 2. Tính tổng tất cả các giá trị nguyên của tham số m để hàm số
x  (m 1)x  3 2m y  đạt cực x  m
tiểu tại x  1.
Câu 3. Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy
trên là hình chữ nhật ABCD , mặt phẳng  ABC song song với mặt phẳng nằm ngang. Khung
sắt đó được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp E ;
A EB; EC; ED
bằng nhau và cùng tạo với mặt phẳng một góc  .
   
Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng F ; F ; F ; F đều 1 2 3 4
có cường độ là 4800N , trọng lượng của cả khung sắt chứa ô tô là 7200 6N . Tính sin (Làm
tròn kết quả đến chữ số hàng phần trăm).
Câu 4. Cho hình tứ diện ABCD có tất cả các cạnh bằng 6. Gọi M , N lần lượt là trung điểm của C , A C .
B P là điểm trên cạnh BD sao cho BP  2P .
D Gọi (H ) là hình giới hạn bởi giao tuyến
của mặt phẳng (MNP) với các mặt của tứ diện ABC .
D Tính diện tích hình (H ) (kết quả làm
tròn đến hàng phần trăm).
Câu 5. Mội người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện trên
một bờ sông thẳng rộng 3 km (như hình vẽ). Anh chèo thuyền đến một điểm D giữa C và B
và sau đó chạy đến B . Biết anh ấy có thể chèo thuyền 6 km/h, chạy 8 km/h và quãng đường
BC  8 km. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người
đàn ông. Khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến B là b a  d trong c đó * a, , b ,
c d  , b là phân số tối giản và d là số nguyên tố. Giá trị của a  b  c  d bằng bao c nhiêu?
Câu 6. Cho hình lăng trụ ABC.AB C
  có đáy là tam giác đều cạnh 2 . Hình chiếu vuông góc của A
lên mặt phẳng  ABC trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường
thẳng AA và BC bằng 3 . Tính thể tích V của khối lăng trụ ABC.AB C
  (kết quả làm tròn 2 đến hàng phần trăm).