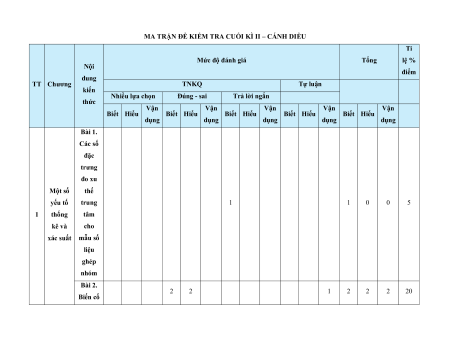
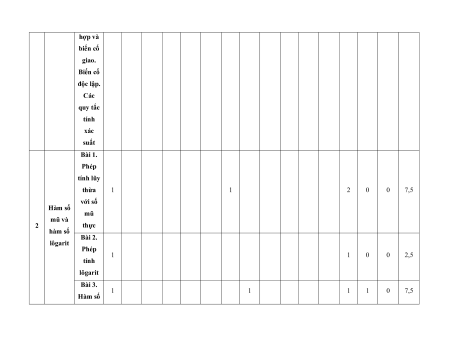
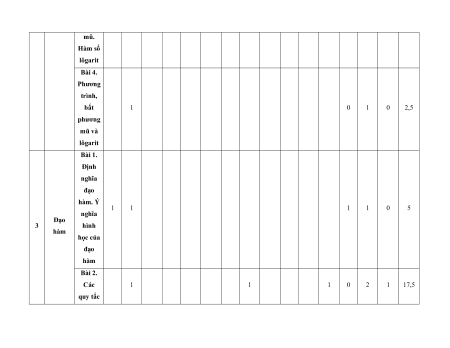
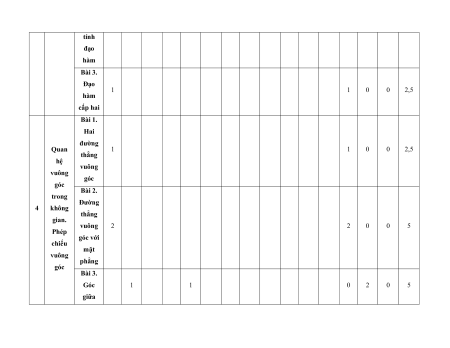
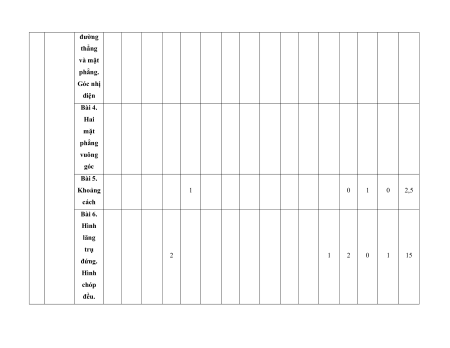
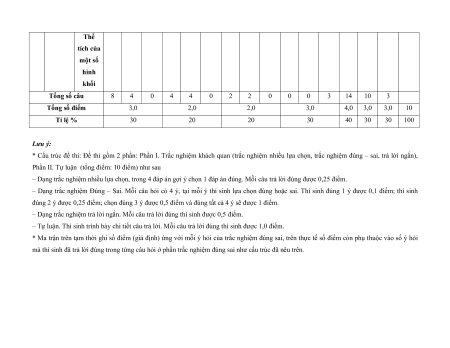
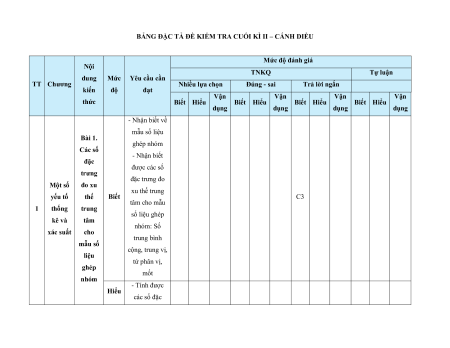
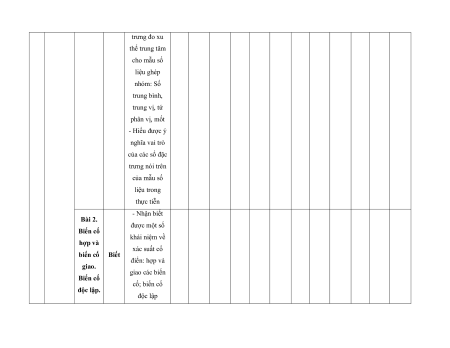
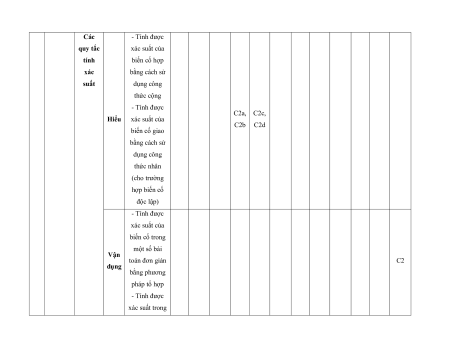
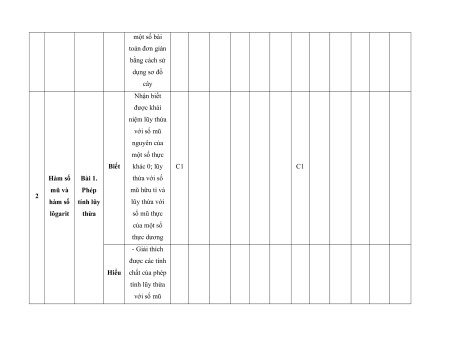
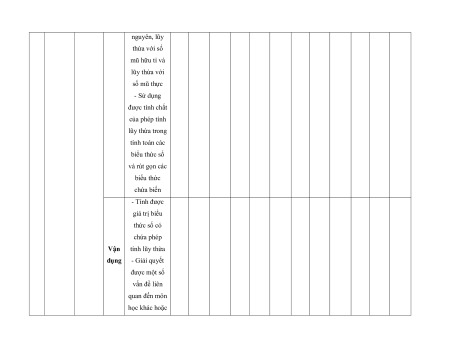
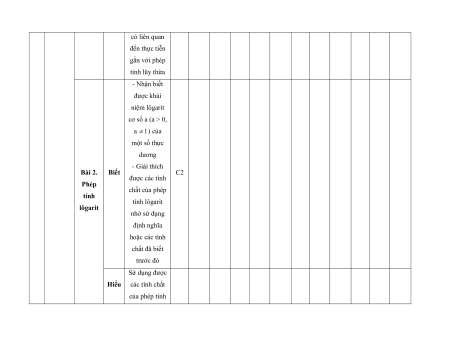
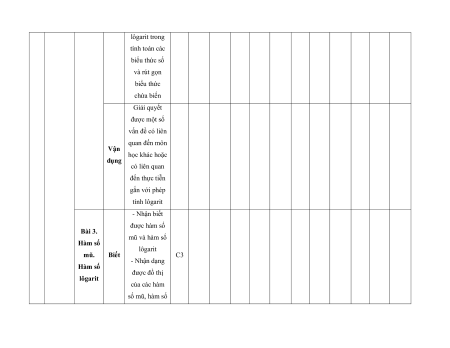
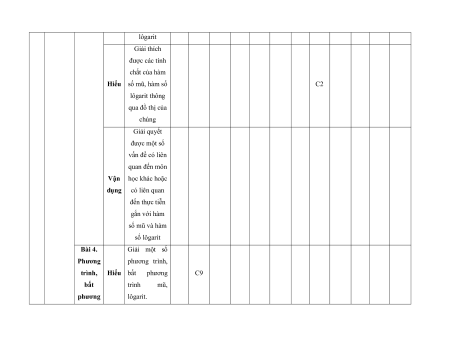
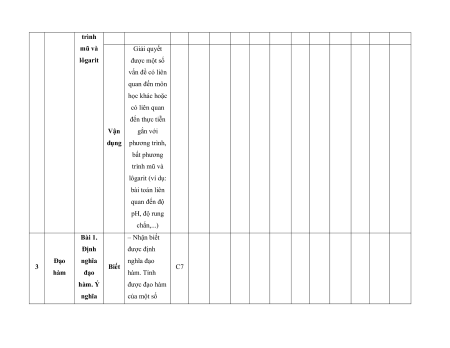
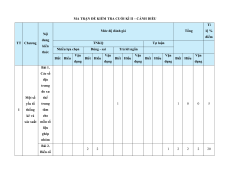
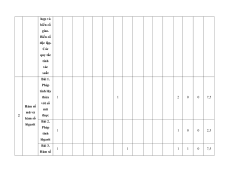
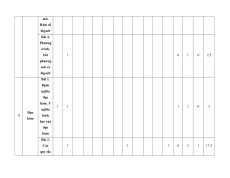
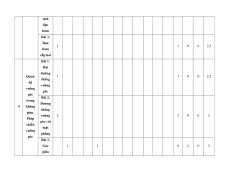
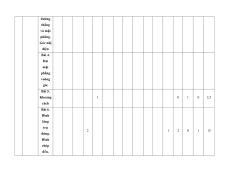
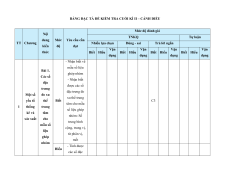
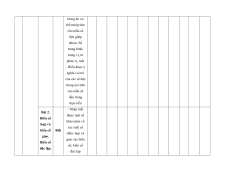
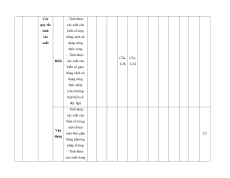
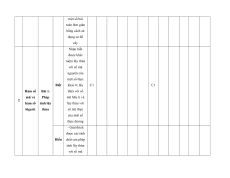
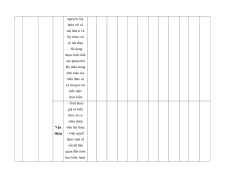
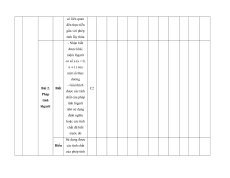
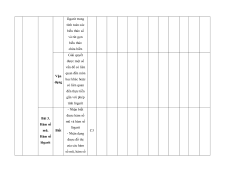
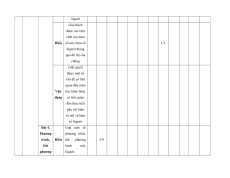
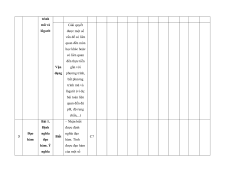
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II – CÁNH DIỀU Tỉ Mức độ đánh giá Tổng lệ % Nội điểm dung TT Chương TNKQ Tự luận kiến Nhiều lựa chọn Đúng - sai Trả lời ngắn thức Vận Vận Vận Vận Vận Biết Hiểu Biết Hiểu Biết Hiểu Biết Hiểu Biết Hiểu dụng dụng dụng dụng dụng Bài 1. Các số đặc trưng đo xu Một số thế yếu tố trung 1 1 0 0 5 1 thống tâm kê và cho xác suất mẫu số liệu ghép nhóm Bài 2. 2 2 1 2 2 2 20 Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất Bài 1. Phép tính lũy thừa 1 1 2 0 0 7,5 với số Hàm số mũ mũ và 2 thực hàm số Bài 2. lôgarit Phép 1 1 0 0 2,5 tính lôgarit Bài 3. 1 1 1 1 0 7,5 Hàm số mũ. Hàm số lôgarit Bài 4. Phương trình, bất 1 0 1 0 2,5 phương mũ và lôgarit Bài 1. Định nghĩa đạo hàm. Ý 1 1 1 1 0 5 nghĩa Đạo 3 hình hàm học của đạo hàm Bài 2. Các 1 1 1 0 2 1 17,5 quy tắc tính đạo hàm Bài 3. Đạo 1 1 0 0 2,5 hàm cấp hai Bài 1. Hai đường Quan 1 1 0 0 2,5 thẳng hệ vuông vuông góc góc Bài 2. trong Đường 4 không thẳng gian. vuông 2 2 0 0 5 Phép góc với chiếu mặt vuông phẳng góc Bài 3. Góc 1 1 0 2 0 5 giữa
15 đề thi Toán 11 Cuối kì 2 Cánh diều cấu trúc mới
288
144 lượt tải
150.000 ₫
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1053587071- NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Bộ tài liệu bao gồm: 10 tài liệu lẻ (mua theo bộ tiết kiệm đến 50%)
- Tailieugiaovien.com.vn giới thiệu bộ 15 đề thi Toán 11 Cuối học kì 2 gồm 10 đề Cấu trúc mới 2025 vầ 5 đề định dạng có tự luận Cánh diều nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 11.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%
Đánh giá
4.6 / 5(288 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
5 đề thi Toán 11 Giữa kì 2 Kết nối tri thức cấu trúc mới90.000 ₫ 133 67 lượt tải
-
Bộ 10 đề thi giữa kì 2 Toán 11 Kết nối tri thức có đáp án150.000 ₫ 4.6 K 2.3 K lượt tải
-
5 đề thi Toán 11 Giữa kì 2 Cánh diều cấu trúc mới90.000 ₫ 92 46 lượt tải
-
5 đề thi Toán 11 Giữa kì 2 Chân trời sáng tạo cấu trúc mới90.000 ₫ 75 38 lượt tải
-
Giáo án Toán 11 Cánh diều | Giáo án Toán 11 mới, chuẩn nhất300.000 ₫ 3.6 K 1.8 K lượt tải
-
Bộ 40 đề thi cuối kì 1 Toán 11 Kết nối tri thức150.000 ₫ 11.6 K 5.8 K lượt tải
-
Chuyên đề Bài tập Toán 11 Kết nối tri thức (Dạy thêm - có lời giải)300.000 ₫ 10.8 K 5.4 K lượt tải
-
Bộ 10 đề thi giữa kì 2 Toán 11 Cánh diều có đáp án150.000 ₫ 2.1 K 1 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 11
Xem thêm-
Bộ 20 đề thi HSG Hóa 11 năm 2023-2024 có đáp án300.000 ₫ 3.4 K 1.7 K lượt tải
-
Bài giảng Powerpoint Lịch sử 11 Cánh diều200.000 ₫ 5.1 K 2.5 K lượt tải
-
Giáo án Lịch sử 11 Cánh diều (năm 2024) | Giáo án Lịch sử 11 mới, chuẩn nhất200.000 ₫ 3.2 K 1.6 K lượt tải
-
Bài giảng Powerpoint Ngữ văn 11 Kết nối tri thức300.000 ₫ 1.7 K 852 lượt tải
-
Bộ 35 Đề thi HSG Sinh học 11 (năm 2024)200.000 ₫ 649 325 lượt tải
-
Bộ 4 đề thi giữa kì 2 Tin học 11 Kết nối tri thức có đáp án70.000 ₫ 5.6 K 2.8 K lượt tải
-
Bài giảng Powerpoint Hóa học 11 Kết nối tri thức200.000 ₫ 3.9 K 2 K lượt tải
-
Chuyên đề dạy thêm Hóa 11 (cấu trúc mới)200.000 ₫ 8 K 4 K lượt tải
Nhắn tin Zalo