Đề thi Toán vào 10 TP.HCM năm 2025 (đề chính thức)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT NĂM 2026
THÀNH PHỐ HỒ CHÍ MINH Môn thi: Toán ĐỀ THAM KHAO
Thời gian làm bài: 120 phút
Bài 1. (1,5 điểm) Cho parabol P 1 2 : y   x . 2
a) Vẽ đô thi P trên hệ trục tọa độ.
b) Tìm tọa độ cac điêm M giao điêm P (khac gôc tọa độ) co hoanh độ băng tung độ.
Bài 2. (1,0 điểm) Cho phương trình 2
x  5x 1  0.
a) Chưng minh phương trình co hai nghiệm phân biệt x , x . 1 2
b) Không giải phương trình, hãy tính gia tri của biêu thưc A  x  x 2  2x  2x . 1 2 1 2
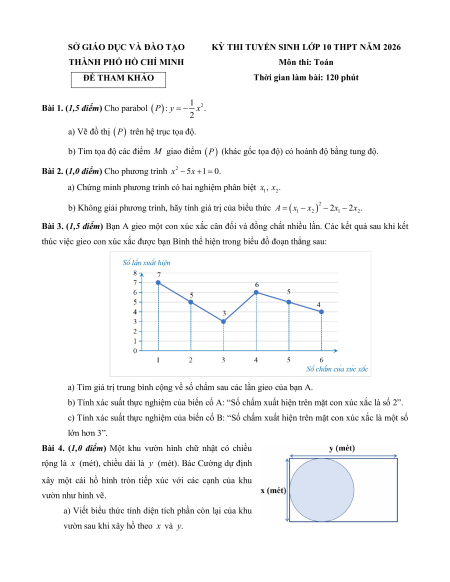
Bài 3. (1,5 điểm) Ban A gieo một con xuc xăc cân đôi va đông chât nhiêu lân. Cac kêt quả sau khi kêt
thuc việc gieo con xuc xăc đươc ban Bình thê hiện trong biêu đô đoan thăng sau:
a) Tìm gia tri trung bình cộng vê sô châm sau cac lân gieo của ban A.
b) Tính xac suât thưc nghiệm của biên cô A: “Sô châm xuât hiện trên măt con xuc xăc la sô 2”.
c) Tính xac suât thưc nghiệm của biên cô B: “Sô châm xuât hiện trên măt con xuc xăc la một sô lơn hơn 3”.
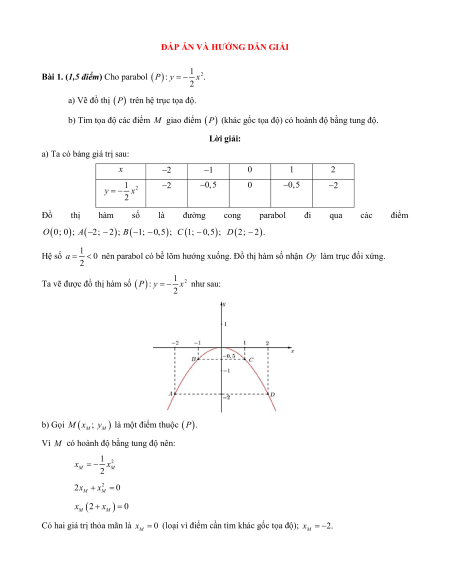
Bài 4. (1,0 điểm) Một khu vươn hình chư nhât co chiêu
rộng la x (met), chiêu dai la y (met). Bac Cương dư đinh
xây một cai hô hình tron tiêp xuc vơi cac canh của khu vươn như hình vẽ.
a) Viêt biêu thưc tính diện tích phân con lai của khu
vươn sau khi xây hô theo x va . y
b) Biêt răng khu vươn hình chư nhât co chiêu dai gâp hai lân chiêu rộng va diện tích phân con lai của khu vươn 2
77,76 m . Tìm cac kích thươc ban đâu của khu vươn. (Lây gia tri   3,14).
Bài 5. (1,0 điểm) Bac Nam co một khôi gô co dang hình trụ vơi chiêu
cao la 40 cm va đương kính đay la 20 cm. Bac Nam muôn tiện khôi gô
nay thanh một vât trang trí co dang hình non co cung chiêu cao va ban
kính vơi khôi hình trụ ban đâu.
a) Tính thê tích phân gô bo đi khi thưc hiện việc tiện gô hình trụ
thanh vât trang trí hình non.
b) Sau khi hoan thanh sản phâm, bac Nam dư tính phun sơn bê
măt bên ngoai của vât trang trí. Tính diện tích cân phải phun sơn (bao gôm cả măt đay).
(Cac kêt qua lam tron chinh xac đên hang phân trăm cua đơn vi)
Biêt công thưc tinh thê tich khôi tru la 2
V   R h (R la ban kinh đay, h la chiêu cao); công thưc tinh thê tich hinh non la 1 2
V   R h; công thưc tinh diên tich xung quanh hinh non la S   Rl (l la đô dai 3 đương sinh).
Bài 6. (1,0 điểm) Hai ban An va Bình đua vơi nhau băng van trươt. Biêt răng nêu cả hai cung dung van
trươt thì tôc độ của An gâp 3 lân của Bình, nhưng tôc độ trươt van của Bình sẽ gâp 3 lân tôc độ chay bộ
của An. Khi tham gia cuộc đua, hai ban xuât phat cung một luc băng van trươt, nhưng sau đo 3 phut,
van trươt của An bi hong va ban ây phải chay bộ vê đích. Biêt răng cả hai ban vê đích cung luc, hoi
cuộc đua đã diên ra trong bao nhiêu phut? (Gia sư tôc đô trươt van, tôc đô chay bô cua An va tôc đô
trươt van cua Binh không thay đôi trong suôt cuôc đua).
Bài 7. (3,0 điểm) Cho tam giac ABC co ba goc nhọn  AB  AC nội tiêp đương tron . O Vẽ đương
kính A của đương tron O va đương cao AH của tam giac ABC.
a) Chưng minh ACD  90 va AB AC  AH  A . D
b) Vẽ CF  AD, chưng minh răng 2
AC  AF  AD va CHF  DCF.
c) Vẽ BK  AC, BK căt AH tai I. Giả sư BAC  60 , BC 10 cm, tính độ dai AI. ----HẾT----
ĐÁP ÁN VÀ HƯỚNG DẪN GIAI
Bài 1. (1,5 điểm) Cho parabol P 1 2 : y   x . 2
a) Vẽ đô thi P trên hệ trục tọa độ.
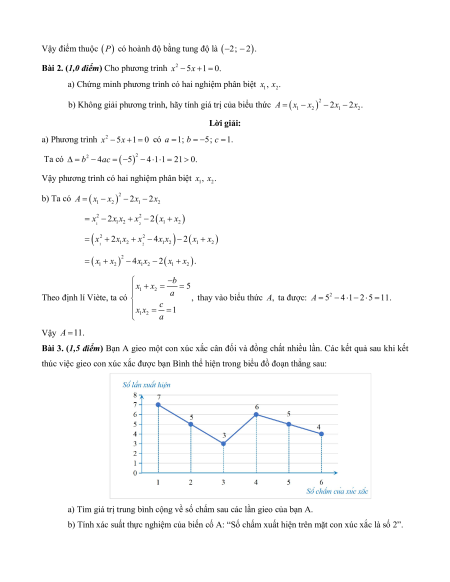
b) Tìm tọa độ cac điêm M giao điêm P (khac gôc tọa độ) co hoanh độ băng tung độ. Lời giải: a) Ta co bảng gia tri sau: x 2  1 0 1 2 1   2 y 0 0,5   x 2  0,5 2  2 Đô thi ham sô la đương cong parabol đi qua cac điêm
O0; 0; A 2  ;  2; B 1
 ;  0,5; C 1;  0,5; D2;  2. Hệ sô 1
a   0 nên parabol co bê lom hương xuông. Đô thi ham sô nhân Oy lam trục đôi xưng. 2
Ta vẽ đươc đô thi ham sô P 1 2
: y   x như sau: 2
b) Gọi M x y
la một điêm thuộc P. M ; M 
Vì M co hoanh độ băng tung độ nên: 1 2 x   x M 2 M 2 2x  x  M M 0 x  x  M  2 M  0
Co hai gia tri thoa mãn la x  (loai vì điêm cân tìm khac gôc tọa độ); x   M 2. M 0
Vây điêm thuộc P co hoanh độ băng tung độ la  2  ;  2.
Bài 2. (1,0 điểm) Cho phương trình 2
x  5x 1  0.
a) Chưng minh phương trình co hai nghiệm phân biệt x , x . 1 2
b) Không giải phương trình, hãy tính gia tri của biêu thưc A  x  x 2  2x  2x . 1 2 1 2 Lời giải: a) Phương trình 2
x  5x 1  0 co a 1; b  5; c 1. Ta co 2
  b  4ac  52  411  21  0.
Vây phương trình co hai nghiệm phân biệt x , x . 1 2
b) Ta co A  x  x 2  2x  2x 1 2 1 2 2 2
 x  2x x  x  2 x  x 1 2  1 2 1 2   2 2
x  2x x  x  4x x  2 x  x 1 2 1 2   1 2  1 2
  x  x 2  4x x  2 x  x . 1 2 1 2  1 2   b x  x   5  1 2
Theo đinh lí Viete, ta co  a  , thay vao biêu thưc , A ta đươc: 2
A  5  41 25 11. c x x  1 1 2  a Vây A 11.
Bài 3. (1,5 điểm) Ban A gieo một con xuc xăc cân đôi va đông chât nhiêu lân. Cac kêt quả sau khi kêt
thuc việc gieo con xuc xăc đươc ban Bình thê hiện trong biêu đô đoan thăng sau:
a) Tìm gia tri trung bình cộng vê sô châm sau cac lân gieo của ban A.
b) Tính xac suât thưc nghiệm của biên cô A: “Sô châm xuât hiện trên măt con xuc xăc la sô 2”.