Chương VI: PHÂN THỨC ĐẠI SỐ
Chủ đề 21: PHÂN THỨC ĐẠI SỐ
Dạng 1: HAI PHÂN THỨC BẰNG NHAU A. PHƯƠNG PHÁP
1. Định nghĩa phân thức đại số
Một phân thức đại số ( hay còn gọi là phân thức) là một biểu thức có dạng A , trong đó A, B là B
những đa thức, và B khác 0.
+ A được gọi là tử thức ( hay tử).
+ B được gọi là mẫu thức ( hay mẫu).
- Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
2. Cách chứng minh hai phân thức bằng nhau
Để chứng minh hai phân thức đại số bằng nhau ra dùng định nghĩa để đưa về chứng minh đẳng thức bằng nhau. Ta có:
+ Với hai phân thức A C A C và ta nói =
nếu A.D = B.C B D B D
- Việc chứng minh hai đằng thức bằng nhau, tác giả đã trình bày ở phần I của trọn bộ sách này.
Những phương pháp và cách thức hiện chứng minh đẳng thức, tác giả đã thực hiện các kỹ
năng đầy dủ ở chương trước.
+ Việc chứng minh một đẳng thức ta áp dụng quy tắc để chứng minh. Có ba trường hợp cần
chứng minh một đẳng thức đúng là: Chứng minh vế trái bằng vế phải, vế phải bằng vế trái, hoặc
cả hai vế cùng bằng một vế nào đó.
+ Tuy nhiên trong kinh nghiệm giải toán của tác giả. Để chứng minh một đẳng thức đúng ta cần
chứng minh vế nào phức tạp rồi dùng các quy tắc tính toán để rút gọn ta đưa đến vế đơn giản hơn. B. BÀI TẬP MẪU
Bài tập mẫu 1: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng: 3 −x − 3 x + 27 = x −1
(1− x)( 2x −3x +9) = (1− x)( 2
x − 3x + 9)(−x − 3) = (−x − 3)( 2
x − 3x + 9)(1− x) a. = −(x + 3)( 2
x − 3x + 9)(1− x) = −( 3 x + 27)(1− x)
( 3x +27)(x− )1
x x ( x + ) 1 b. = 2 x − 2 x − x − 2 Hướng dẫn giải
a. Ta cần chứng minh: x ( 2
x + x) = ( x + ) 2 2 2 x
Cách 1: VT = x ( 2 x + x) 3 2 2 = x + 2x VP = ( x + ) 2 3 2
2 x = x + 2x Vậy: x ( 2
x + x) = ( x + ) 2 2 2 x
Do đó theo định nghĩa thì: 2 x x = 2 x + 2 x + 2x
Cách 2: VT = x ( 2 x + 2x) = . x x ( x + 2) = 2
x ( x + 2) = ( x + ) 2 2 x Vậy: 2 x x = 2 x + 2 x + 2x
b. Ta cần chứng minh : x ( 2
x − x − 2) = x ( x − 2)( x + ) 1
Cách 1: VT = x ( 2 x − x − ) 3 2
2 = x − x − 2x
VP = x ( x − )( x + ) = ( 2
x − x)( x + ) 3 2 2 1 2
1 = x − x − 2x Vậy: x ( 2
x − x − 2) = x ( x − 2)( x + ) 1 Do đó: x x ( x + ) 1 = 2 x − 2 x − x − 2
Cách 2: VP = x ( x − )( x + ) = x ( x − )( x + ) = x ( 2 2 1 2 1
x − x − 2) = VT x x ( x + ) 1 Vậy: = 2 x − 2 x − x − 2
Bài tập mẫu 2: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng: 2 x + y x + xy (x − ) 1 ( y − x) 1− x a. = b. = 2 xy −1 x y − x (x − y)2 x − y Hướng dẫn giải
a. Cần chứng minh : ( x + y)( 2
x y − x) = ( xy − )( 2 1 x + xy )
Cách 1: VT = ( + )( 2 x y x y − x) = 3 2 2 2
x y − x + x y − xy VP = ( xy − )( 2 x + xy ) 3 2 2 2 3 2 2 2 1
= x y + x y − x − xy = x y − x + x y − xy Do đó: VT = VP 2 x + y x + xy Vậy: = 2 xy −1 x y − x
Cách 2: Ta có: VT = ( x + y)( 2
x y − x) = ( x + y) x ( xy − ) = ( 2
x + xy )( xy − ) = (xy − )( 2 1 1 1 x + xy ) =VP Do đó: VT = VP 2 x + y x + xy Vậy: = 2 xy −1 x y − x 2
b. Ta cần chứng minh: ( x − )
1 ( y − x)( x − y) = ( x − y) (1− x) Cách 1: VT = ( 2 − − + )( − ) 2 2 3 2 2 2 xy x y x x
y = x y − xy − x + x y − xy + y + x − xy 2 2 3 2 2
= 2x y − xy − x − 2xy + y + x VP 2 2 3 2 2
= 2x y − xy − x − 2xy + y + x 2 2 3 2 2
= 2x y − xy − x − 2xy + y + x Do đó: VT = VP (x − ) 1 ( y − x) 1− x Vậy: = ( x − y)2 x − y
Cách 2: VT = ( x − )
1 ( y − x)( x − y) = − (1− x) − ( x − y) ( x − y)
= ( − x)( x − y)( x − y) = ( − x)( x − y)2 1 1 2
= ( x − y) (1− x) Do đó: VT = VP (x − ) 1 ( y − x) − Vậy: 1 x = ( x − y)2 x − y
Bài tập mẫu 3: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng: 2x ( 2 x + ) 1 2x 2 2 x − 5x + 6 x + 2x − 8 a. = ( = b. 2x − 3)( 2 x + ) 1 2x − 3 x + 3 x − 4
Hướng dẫn giải
a. Ta cần chứng minh: x ( 2
x + )( x − ) = x ( x − )( 2 2 1 2 3 2 2 3 x + ) 1 VT = x ( 2
x + )( x − ) = ( 3 2 1 2 3
2x + 2x)(2x − 3) 4 3 2
= 4x − 6x + 4x + 6x
VP = x ( x − )( 2 x + ) = ( 2 x − x)( 2 2 2 3 1 4 6 x + ) 1 4 3 2
= 4x − 6x + 4x − 6x Do đó: VT = VP 2x ( 2 x + ) 1 2x Nên: ( = 2x − 3)( 2 x + ) 1 2x − 3 b. Ta cần chứng minh: ( 2
x − x + )( x + ) = ( x − )( 2 5 6 4 3 x + 2x − 8) Cách 1: VT = ( 2
x − x + )( x + ) 3 2 2 5 6
4 = x + 4x − 5x − 20x + 6x + 24 3 2
= x − x −14x + 24 VP = ( x − )( 2 x + x − ) 3 2 2 3 2
8 = x + 2x − 8x − 3 x − 6x + 24 3 2
= x − x −14x + 24 Do đó: VT = VP 2 2 x − 5x + 6 x + 2x − 8 Nên: = x + 3 x − 4 Cách 2: VT = ( 2
x − 5x + 6)( x + 4) = x( x − 3) − 2( x − 3) ( x + 4)
= ( x − 3)( x − 2)( x + 4) = ( x − 3) ( x − 2)( x + 4) = ( x − )( 2 3
x + 2x − 8) = VP Do đó: VT = VP 2 2 x − 5x + 6 x + 2x − 8 Nên: = x + 3 x − 4 A C
Nhận xét: Để chứng tỏ hai phân thức và
bằng nhau, ta có thể dùng một trong hai cách sau: B D
Cách 1: Tính A.D và B.C để thấy rằng cách tích này đều cho ta cùng một kết quả.
Cách 2: Từ một trong hai tích A.D hoặc B.C ( cần có sự lựa chọn sao cho thuận lợi trong các biến
đổi), bằng cachs sử dụng các phép tính của đa thức như: phép nhân, phân tích đa thức thành nhân tử
... để biến đổi tích này thành tích kia.
Phương pháp giải Toán 8 (cơ bản, nâng cao) Học kì 2
1 K
510 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Bộ tài liệu bao gồm: 5 tài liệu lẻ (mua theo bộ tiết kiệm đến 50%)
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ Chuyên đề Phương pháp giải Toán 8 từ cơ bản đến nâng cao gồm các dạng bài tập với phương pháp giải chi tiết nhằm giúp Giáo viên có thêm tài liệu tham khảo.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1019 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 8
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Chương VI: PHÂN THỨC ĐẠI SỐ
Chủ đề 21: PHÂN THỨC ĐẠI SỐ
Dạng 1: HAI PHÂN THỨC BẰNG NHAU
A. PHƯƠNG PHÁP
1. Định nghĩa phân thức đại số
Một phân thức đại số ( hay còn gọi là phân thức) là một biểu thức có dạng
A
B
, trong đó A, B là
những đa thức, và B khác 0.
+ A được gọi là tử thức ( hay tử).
+ B được gọi là mẫu thức ( hay mẫu).
- Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
2. Cách chứng minh hai phân thức bằng nhau
Để chứng minh hai phân thức đại số bằng nhau ra dùng định nghĩa để đưa về chứng minh đẳng
thức bằng nhau.
Ta có:
+ Với hai phân thức
A
B
và
C
D
ta nói
A
B
=
C
D
nếu A.D = B.C
- Việc chứng minh hai đằng thức bằng nhau, tác giả đã trình bày ở phần I của trọn bộ sách này.
Những phương pháp và cách thức hiện chứng minh đẳng thức, tác giả đã thực hiện các kỹ
năng đầy dủ ở chương trước.
+ Việc chứng minh một đẳng thức ta áp dụng quy tắc để chứng minh. Có ba trường hợp cần
chứng minh một đẳng thức đúng là: Chứng minh vế trái bằng vế phải, vế phải bằng vế trái, hoặc
cả hai vế cùng bằng một vế nào đó.
+ Tuy nhiên trong kinh nghiệm giải toán của tác giả. Để chứng minh một đẳng thức đúng ta cần
chứng minh vế nào phức tạp rồi dùng các quy tắc tính toán để rút gọn ta đưa đến vế đơn giản
hơn.
B. BÀI TẬP MẪU
Bài tập mẫu 1: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a.
( )
( )
( )
( )
( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
3
2
22
23
3
3 27
1
1 3 9
1 3 9 3 3 3 9 1
3 3 9 1 27 1
27 1
xx
x
x x x
x x x x x x x x
x x x x x x
xx
− − +
=
−
− − +
= − − + − − = − − − + −
= − + − + − = − + −
+−
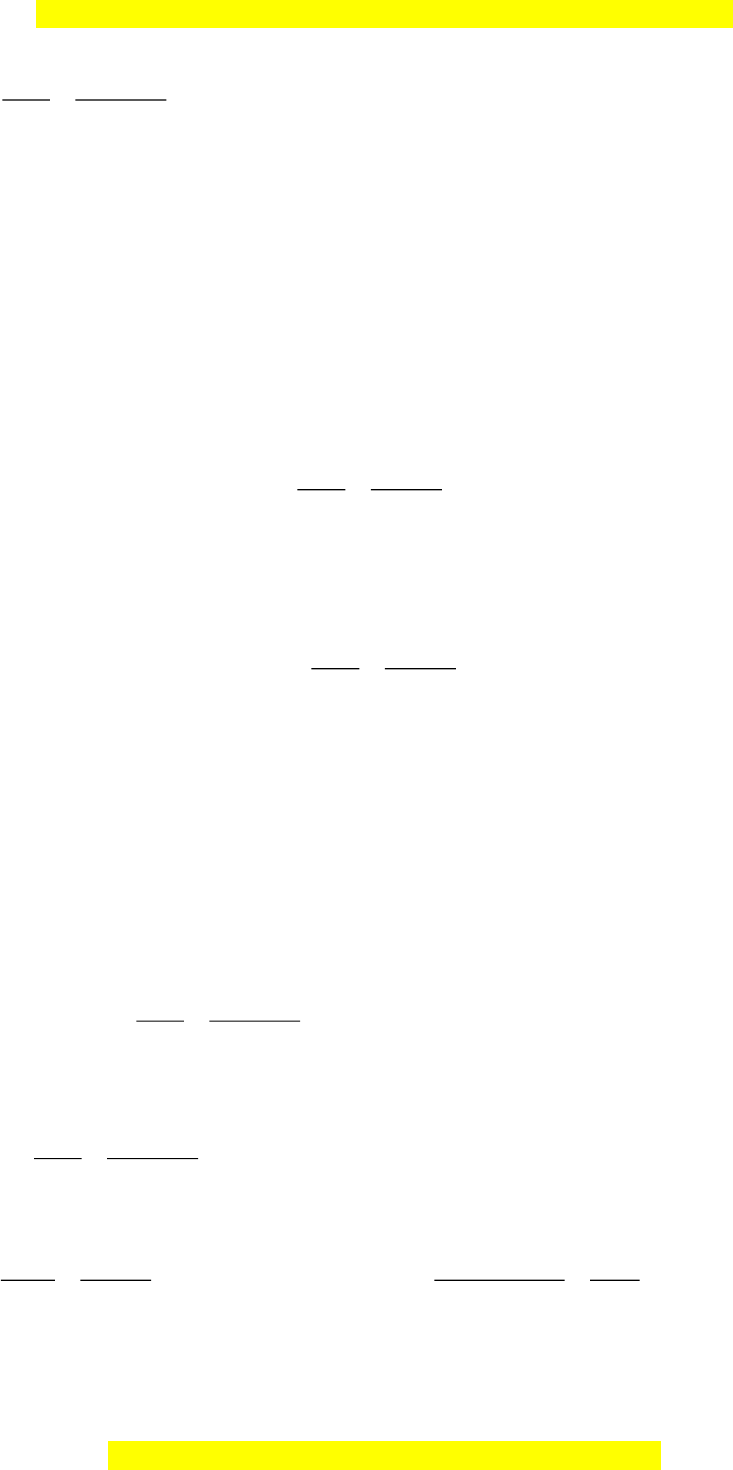
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
b.
( )
2
1
22
xx
x
x x x
+
=
− − −
Hướng dẫn giải
a. Ta cần chứng minh:
( )
( )
22
22x x x x x+ = +
Cách 1: VT =
( )
2 3 2
22x x x x x+ = +
VP =
( )
2 3 2
22x x x x+ = +
Vậy:
( )
( )
22
22x x x x x+ = +
Do đó theo định nghĩa thì:
2
2
22
xx
x x x
=
++
Cách 2: VT =
( )
2
2x x x+
=
( )
.2x x x+
=
( )
2
2xx+
=
( )
2
2xx+
Vậy:
2
2
22
xx
x x x
=
++
b. Ta cần chứng minh :
( )
( )( )
2
2 2 1x x x x x x− − = − +
Cách 1: VT =
( )
2 3 2
22x x x x x x− − = − −
VP =
( )( )
( )
( )
2 3 2
2 1 2 1 2x x x x x x x x x− + = − + = − −
Vậy:
( )
( )( )
2
2 2 1x x x x x x− − = − +
Do đó:
( )
2
1
22
xx
x
x x x
+
=
− − −
Cách 2: VP =
( )( ) ( )( )
( )
2
2 1 2 1 2x x x x x x x x x− + = − + = − −
= VT
Vậy:
( )
2
1
22
xx
x
x x x
+
=
− − −
Bài tập mẫu 2: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a.
2
2
1
x y x xy
xy x y x
++
=
−−
b.
( )( )
( )
2
1
1
x y x
x
xy
xy
−−
−
=
−
−
Hướng dẫn giải
a. Cần chứng minh :
( )
( )
( )
( )
22
1x y x y x xy x xy+ − = − +

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Cách 1: VT =
( )
( )
2
x y x y x+−
=
3 2 2 2
x y x x y xy− + −
VP =
( )
( )
2 3 2 2 2 3 2 2 2
1xy x xy x y x y x xy x y x x y xy− + = + − − = − + −
Do đó: VT = VP
Vậy:
2
2
1
x y x xy
xy x y x
++
=
−−
Cách 2: Ta có: VT =
( )
( )
( ) ( )
( )
( ) ( )
( )
2 2 2
1 1 1x y x y x x y x xy x xy xy xy x xy+ − = + − = + − = − +
=VP
Do đó: VT = VP
Vậy:
2
2
1
x y x xy
xy x y x
++
=
−−
b. Ta cần chứng minh:
( )( )( ) ( ) ( )
2
11x y x x y x y x− − − = − −
Cách 1: VT
=
( )
( )
2 2 2 3 2 2 2
xy x y x x y x y xy x x y xy y x xy− − + − = − − + − + + −
2 2 3 2 2
22x y xy x xy y x= − − − + +
VP
2 2 3 2 2
22x y xy x xy y x= − − − + +
2 2 3 2 2
22x y xy x xy y x= − − − + +
Do đó: VT = VP
Vậy:
( )( )
( )
2
1
1
x y x
x
xy
xy
−−
−
=
−
−
Cách 2: VT
=
( )( )( ) ( ) ( ) ( )
11x y x x y x x y x y− − − = − − − − −
( )( )( ) ( )( )
2
11x x y x y x x y= − − − = − −
( ) ( )
2
1x y x= − −
Do đó: VT = VP
Vậy:
( )( )
( )
2
1
1
x y x
x
xy
xy
−−
−
=
−
−
Bài tập mẫu 3: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a.
( )
( )
( )
2
2
21
2
23
2 3 1
xx
x
x
xx
+
=
−
−+
b.
22
5 6 2 8
34
x x x x
xx
− + + −
=
+−

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Hướng dẫn giải
a. Ta cần chứng minh:
( )
( ) ( )
( )
22
2 1 2 3 2 2 3 1x x x x x x+ − = − +
VT
( )
( )
( )
( )
23
2 1 2 3 2 2 2 3x x x x x x= + − = + −
4 3 2
4 6 4 6x x x x= − + +
VP
( )
( ) ( )( )
2 2 2
2 2 3 1 4 6 1x x x x x x= − + = − +
4 3 2
4 6 4 6x x x x= − + −
Do đó: VT = VP
Nên:
( )
( )
( )
2
2
21
2
23
2 3 1
xx
x
x
xx
+
=
−
−+
b. Ta cần chứng minh:
( )
( ) ( )
( )
22
5 6 4 3 2 8x x x x x x− + + = − + −
Cách 1: VT
( )
( )
2 3 2 2
5 6 4 4 5 20 6 24x x x x x x x x= − + + = + − − + +
32
14 24x x x= − − +
VP
( )
( )
2 3 2 2
3 2 8 2 8 3 6 24x x x x x x x x= − + − = + − − − +
32
14 24x x x= − − +
Do đó: VT = VP
Nên:
22
5 6 2 8
34
x x x x
xx
− + + −
=
+−
Cách 2: VT
( )
( ) ( ) ( ) ( )
2
5 6 4 3 2 3 4x x x x x x x= − + + = − − − +
( )( )( ) ( ) ( )( )
3 2 4 3 2 4x x x x x x= − − + = − − +
( )
( )
2
3 2 8x x x= − + −
= VP
Do đó: VT = VP
Nên:
22
5 6 2 8
34
x x x x
xx
− + + −
=
+−
Nhận xét: Để chứng tỏ hai phân thức
A
B
và
C
D
bằng nhau, ta có thể dùng một trong hai cách sau:
Cách 1: Tính A.D và B.C để thấy rằng cách tích này đều cho ta cùng một kết quả.
Cách 2: Từ một trong hai tích A.D hoặc B.C ( cần có sự lựa chọn sao cho thuận lợi trong các biến
đổi), bằng cachs sử dụng các phép tính của đa thức như: phép nhân, phân tích đa thức thành nhân tử
... để biến đổi tích này thành tích kia.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài tập mẫu 4: Các phân thức sau có bằng nhau hay không?
a.
2
2
32
2
xx
xx
−+
−
;
1
;
x
x
−
2
2
65
5
xx
xx
−+
−
b.
2
2
3 7 4
43
xx
xx
−+
−+
;
2
2
3 5 2
;
56
xx
xx
−+
−+
34
3
x
x
−
−
Hướng dẫn giải
a. Nhận xét:
( ) ( )
( )
22
3 2 2 1x x x x x x− + = − −
Ta có: VT
( )
2 3 2
3 2 3 2x x x x x x= − + = − +
và VP
( )
( )
2 3 2
2 1 3 2x x x x x x= − − = − +
Do đó: VT = VP.
Vậy:
2
2
32
2
xx
xx
−+
−
=
1x
x
−
Tương tự:
1x
x
−
=
2
2
65
5
xx
xx
−+
−
b. Dễ thấy:
2
2
3 7 4
43
xx
xx
−+
−+
=
34
3
x
x
−
−
Mặt khác:
2
2
3 5 2
56
xx
xx
−+
−+
34
3
x
x
−
−
Vì vậy:
22
22
3 7 4 3 5 2
4 3 5 6
x x x x
x x x x
− + − +
− + − +
Nhận xét: Khi gặp dạng bài này mà có nhiều hơn hai phân thức ta cần lựa chọn phân thức trung
gian để Thực hiện các phép nhân dễ dàng hơn.
Chẳng hạn trong bài tập trên; ở bài a phân thức trung gian là
1x
x
−
; còn ở bài b là
34
3
x
x
−
−
.
Bài tập mẫu 5: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a.
22
7 6 2 7 5
6 2 5
x x x x
xx
− + − +
=
−−
b.
( )
( )
3
2
3 27
1
1 3 9
xx
x
x x x
− − +
=
−
− − +
Hướng dẫn giải
a. Ta cần chứng minh:
( )
( )
( )
( )
22
7 6 2 5 2 7 5 6x x x x x x− + − = − + −
Ta có: VT
( )
( )
( )
( )
22
7 6 2 5 6 6 2 5x x x x x x x= − + − = − − + −
( ) ( ) ( ) ( )( )( )
6 6 2 5 6 1 2 5x x x x x x x= − − − − = − − −
( )
( )
2
6 2 7 5x x x= − − +
= VP
Vậy hai phân thức đó bằng nhau.
b. Ta cần chứng minh:
( )
( )
( )
( )
( )
23
1 3 9 3 27 1x x x x x x− − + − − = + −

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có: VT
( )
( )
( ) ( )
( )
( )
22
1 3 9 3 3 3 9 1x x x x x x x x= − − + − − = − − − + −
( )
( )
( )
( )
( )
23
3 3 9 1 27 1x x x x x x= − + − + − = − + −
=
( )
( )
3
27 1xx+−
= VP
Vậy đẳng thức được chứng minh.
Bài tập mẫu 6: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a.
( )
( )
3
2
28
5
5 2 4
xx
x
x x x
−−
=
−
− + +
b.
32
32
4 4 1
7 14 8 2
x x x x
x x x x
− − + +
=
− + − −
Hướng dẫn giải
a. Ta cần chứng minh:
( )
( )
( ) ( )
( )
23
5 2 4 2 5 8x x x x x x− + + − = − −
Ta có VP
( )
( )
( )
( )
( )
32
5 8 2 2 4 5x x x x x x= − − = − + + −
( )
( )
( )
( )
( )
2
2 2 4 5x x x x= − − + + − −
( )
( )
( )
2
5 2 4 2x x x x= − + + −
= VT
Vậy đẳng thức được chứng minh.
b. Ta cần chứng minh:
( )
( )
( )
3 2 3 2
4 4 9 2 1 7 14 8x x x x x x x x− − + − = + − + −
Ta có: VT
( )
( )
( )
( )
3 2 3 2 2
4 4 2 5 5 4 4 2x x x x x x x x x x= − − + − = + − − + + −
( ) ( ) ( ) ( )
2
1 5 1 4 1 2x x x x x x
= + − + + + −
( )
( )
( )
2
1 5 4 2x x x x= + − + −
( )
( )
32
1 7 14 8x x x x= + − + −
= VP
Vậy :
32
32
4 4 1
7 14 8 2
x x x x
x x x x
− − + +
=
− + − −
Chú ý: Đối với những bài phân tích đa thức thành nhân tử khá khó khăn chúng ta có thể chứng
minh hai đẳng thức bằng nhau bằng cách biến đổi hai vế của đẳng
thức thành biểu thức giống nhau. Để đạt đến mục đích cuối cùng là chứng mình đẳng thức.
Thật vậy đối với bài toán này cần chứng minh như sau:
( )
( ) ( )
( )
3 2 3 2
4 4 2 1 7 14 8x x x x x x x x− − + − = + − + −
Ta có:
VT
4 3 3 2 2 4 3 2
2 4 8 2 4 8 6 7 6 8x x x x x x x x x x x= − − + − + + − = − + + −

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
VP
4 3 3 2 2 4 3 2
7 7 14 14 8 8 6 7 6 8x x x x x x x x x x x= + − − + + − − = − + + −
Vậy sau khi biến đổi ta thấy vế trái và vế phải đều bằng
4 3 2
6 7 6 8x x x x− + + −
Vậy :
32
32
4 4 1
7 14 8 2
x x x x
x x x x
− − + +
=
− + − −
Bài tập mẫu 7: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
2
34
1
3 3 36 3
x
x x x
−
=
− − +
, nếu
4x
;
2
34
1
3 3 36 3
x
x x x
−
−
=
− − +
, nếu
4x
.
Hướng dẫn giải
*) Vì
4 4 4x x x − = −
.
Khi đó:
2
34
1
3 3 36 3
x
x x x
−
=
− − +
( )
2
34
1
3 3 36 3
x
x x x
−
=
− − +
Ta cần chứng minh:
( )( )
2
3 4 3 3 3 36x x x x− + = − −
( )
22
3 3 4 12 3 3 36x x x x x+ − + = − −
( )
22
3 12 3 3 36x x x x− + = − −
22
3 3 36 3 3 36x x x x− − = − −
Vậy đẳng thức được chứng minh.
*) Vì
4x
thì
( )
| 4| 4 4x x x− = − − = −
Khi đó:
2
34
1
3 3 36 3
x
x x x
−
−
=
− + +
Nên:
( )
2
34
1
3 3 36 3
x
x x x
−
−
=
− + +
Ta cần chứng minh:
( )( )
( )
2
3 4 3 3 3 36x x x x− + = − − +
( ) ( )
22
3 4 12 3 3 3 36x x x x x+ − − = − − +
( ) ( )
22
3 12 3 3 36x x x x− + + = − − +
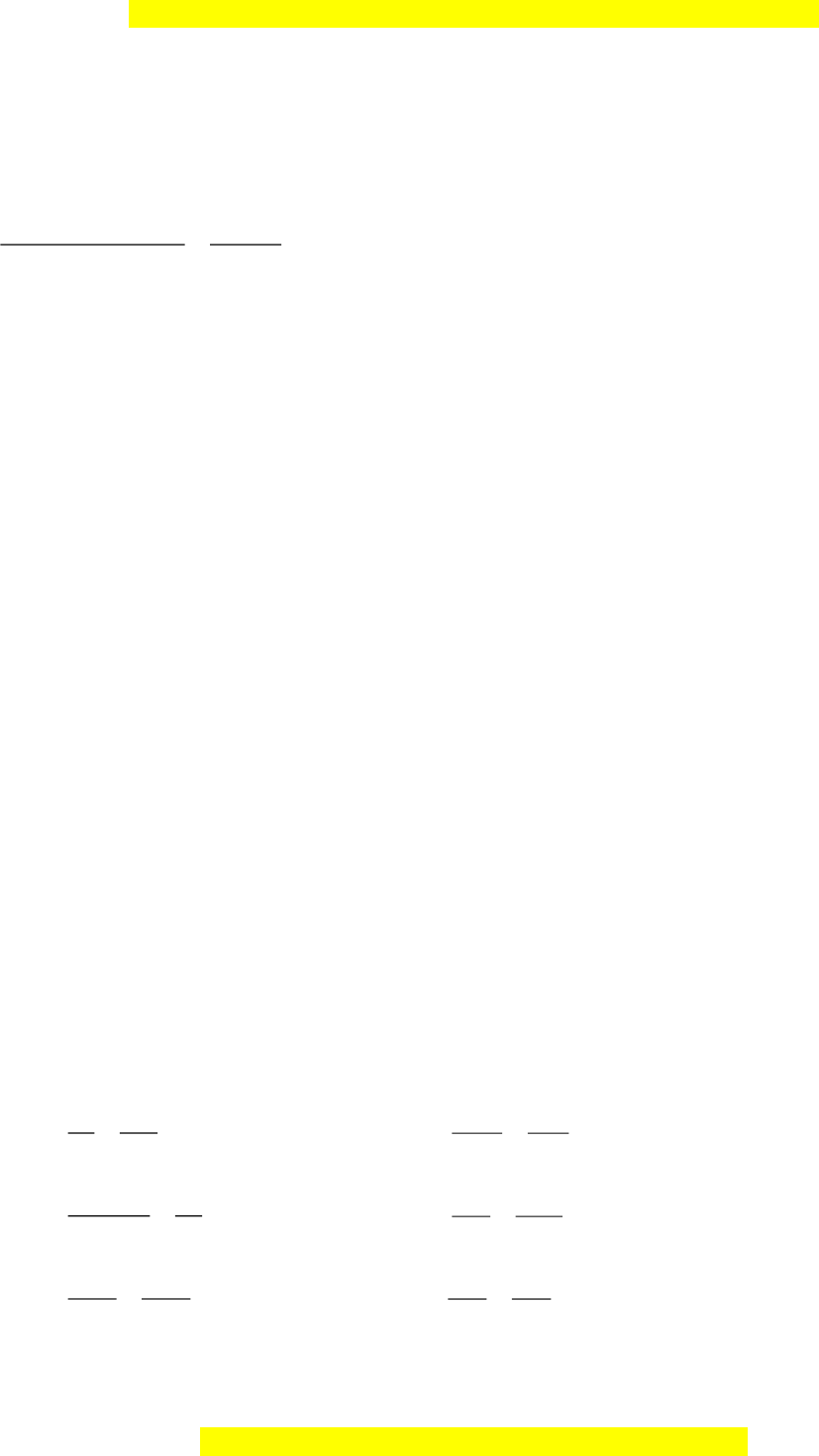
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
( ) ( )
22
3 3 36 3 3 36x x x x− − + = − − +
Vậy đẳng thức được chứng minh.
Bài tập mẫu 8: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
( )
2
43
4 3 2 2
1
1
2 1 1
x
x x x
x x x x x
+
+ + +
=
− + − + +
Hướng dẫn giải
Ta cần chứng minh:
( )( )
( )
( )
2
4 3 2 4 3 2
1 1 1 2 1x x x x x x x x x+ + + + = + − + − +
Ta có: VP
( )
( )
2
4 3 2
1 2 1x x x x x= + − + − +
( )
( )
2
4 2 3 2
11x x x x x x= + + − − + +
( )
( ) ( ) ( )
2
2 2 2 2
1 1 1 1x x x x x x
= + + − + + +
( )
( )( )
2
22
1 1 1x x x x= + + − +
( )
( )
( )
( )
22
1 1 1 1x x x x x= + + + − +
( )
( )( )
23
1 1 1x x x= + + +
Mặt khác: VT
( )( )
4 3 2
11x x x x= + + + +
( )
( )
( )
4 3 2
11x x x x
= + + + +
( ) ( )
( )
32
1 1 1x x x x
= + + + +
( )
( )( )
23
1 1 1x x x= + + +
Vậy đẳng thức được chứng minh.
C. BÀI TẬP LUYỆN TẬP
Bài tập 1: Chứng minh các đẳng thức sau:
a.
( )
3 6x
0
4 8x
yy
x=
b.
( )
22
3x 3x
0
22
y
yy
−
=
−
c.
( )
( )
( )
2
2
33
xy
xy
yx
−
−
=
−
d.
( )
2
2x 8x
0, 0
3a 12a
yy
ay
y
=
e.
( )
11
2
22
xx
y
yy
−−
=
−−
f.
( )
2a 2a
0
55
b
bb
−
=
−
Bài tập 2: Chứng minh các đẳng thức sau:

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a.
( )
( )
33
2
22
0
2x 4
xx
x
x
xx
−−
=
−
++
b.
( )
( )
22
3
3
x x y
x
xy
x y y x
−−
=
+−
c.
( )
( )
2
2
3a( )
0,
3a 9a
x y x y
a x y
xy
++
= −
+
Bài tập 3: Các phân thức sau có bằng nhau không ? Vì sao ?
a.
2
1
1
x
x
+
−
và
1
1x −
b.
3
2x +
và
2
2
4
x
x
−
−
D. HƯỚNG DẪN GIẢI HOẶC ĐÁP SỐ
Bài tập 1: Ta thấy:
a.
24 24xy xy=
b.
22
66x y x y=
c.
( ) ( )
66x y x y− = −
d.
22
24 24axy axy=
e.
( )( ) ( )( )
1 2 1 2x y x y− − = − −
f.
10 10ab ab=
Bài tập 2: Chứng minh các đẳng thức sau:
a.
( )
( )
( )
( )
22
2 2x 4 2 2 4x x x x x x x− + + = − + +
b.
( ) ( )
2 2 2 2
33x y x x y x− = −
c.
( ) ( )
22
9a 9 9a 9xx+ = +
Bài tập 3: a. Bằng nhau vì:
22
11xx− = −
b. Không bằng nhau và
( )
( )( )
2
3 4 2 2x x x− + −



























