TUYỂN TẬP 60 ĐỀ THI
HỌC KỲ II LỚP 9 -MÔN TOÁN
Người tổng hợp, sưu tầm : Thầy giáo Hồ Khắc Vũ
ĐỀ SỐ 001 Câu 1.(1,5đ) a) Rút gọn : A= 2 - 4 +5
b) Rút gọn biểu thức B = +
Câu 2.(1,5 điểm) Giải hệ phương trình:
Câu 3.(2,0 điểm) Giải bài toán bằng các lập phương trình hoặc hệ phương trình:
Quảng đường từ A đến B dài 120km . Hai ôtô khởi hành cùng một lúc đi từ
A đến B .Ôtô thứ nhất chạy nhanh hơn ôtô thứ hai 12km/h nên đến nơi sớm hơn Ôtô
thứ hai 30 phút. Tính vận tốc mỗi xe.
Câu 4.(1,5 điểm) Cho phương trình x2 + 2(m-1) – m2 =0 với m là tham số.
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt.
b) Giả sử phương trình có hai nghiệm là x 2 2
1, x2, hãy tính x1 + x2 theo m.
Câu 5.(3,5 điểm) Cho đường tròn O, bán kính R. Từ một điểm M ở ngoài đường tròn
(O) sao cho MO = 2R, ta kẽ hai tiếp tuyến MA và MB (A và B là tiếp điểm).
Một cát tuyến bất kỳ qua M cắt đường tròn tại C và D . Kẻ tia phân giác của
cắt dây CD tại E và đường tròn tại N.
a).Chứng minh tứ giác OAMB nội tiếp được. b).Chứng minh MA = ME
c).Tính tích số MC.MD theo R. =HẾT=
ĐÁP ÁN ĐỀ SỐ 001
II- Đáp án và thang điểm: CÂU ĐÁP ÁN ĐIỂM Câu 1a. - 4 +5 (0,75đ) = 2 - 4 +5 0,25 = 2.3 -4.4 +5.5 0,25 = 6 - 16 +25 = 15 0,25 Câu 1b. (0,75đ) B = + 0,25 = = 0,25 = = 3 0,25 Câu 2. 0,75 (1,5đ)
Vậy hệ pt có nghiệm duy nhất (x,y) = (1,2) 0,75 Câu 3.
Gọi x km/h là vận tốc của ôtô thưa nhất, điều kiện x > 12 0,25 (2,0đ)
Vận tốc của ôtô thứ hai là x -12 km/h. 0,25
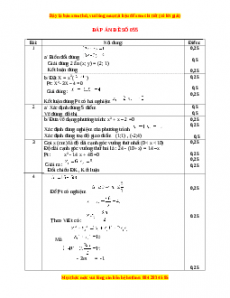
Thời gian ôtô thứ nhất đi từ A đến B (giờ)
0,25
Thời gian ôtô thứ hai đi từ A đến B (giờ) 0,25
Vì ôtô thứ nhất đến nơi sớm hơn ôtô thứ hai 30 phút= giờ nên 0,25 ta có phương trình - =
Rút gọn phương trình ta được: x2 -12x -2880 = 0
Giải ra ta được x1 = 60 (nhận), x2 = -48 (loại)
Vậy vận tốc của xe thứ nhất là 60 km/h, vận tốc của xe thứ hai là 60-12 = 48 km/h 0,50 0,25 Câu 4a
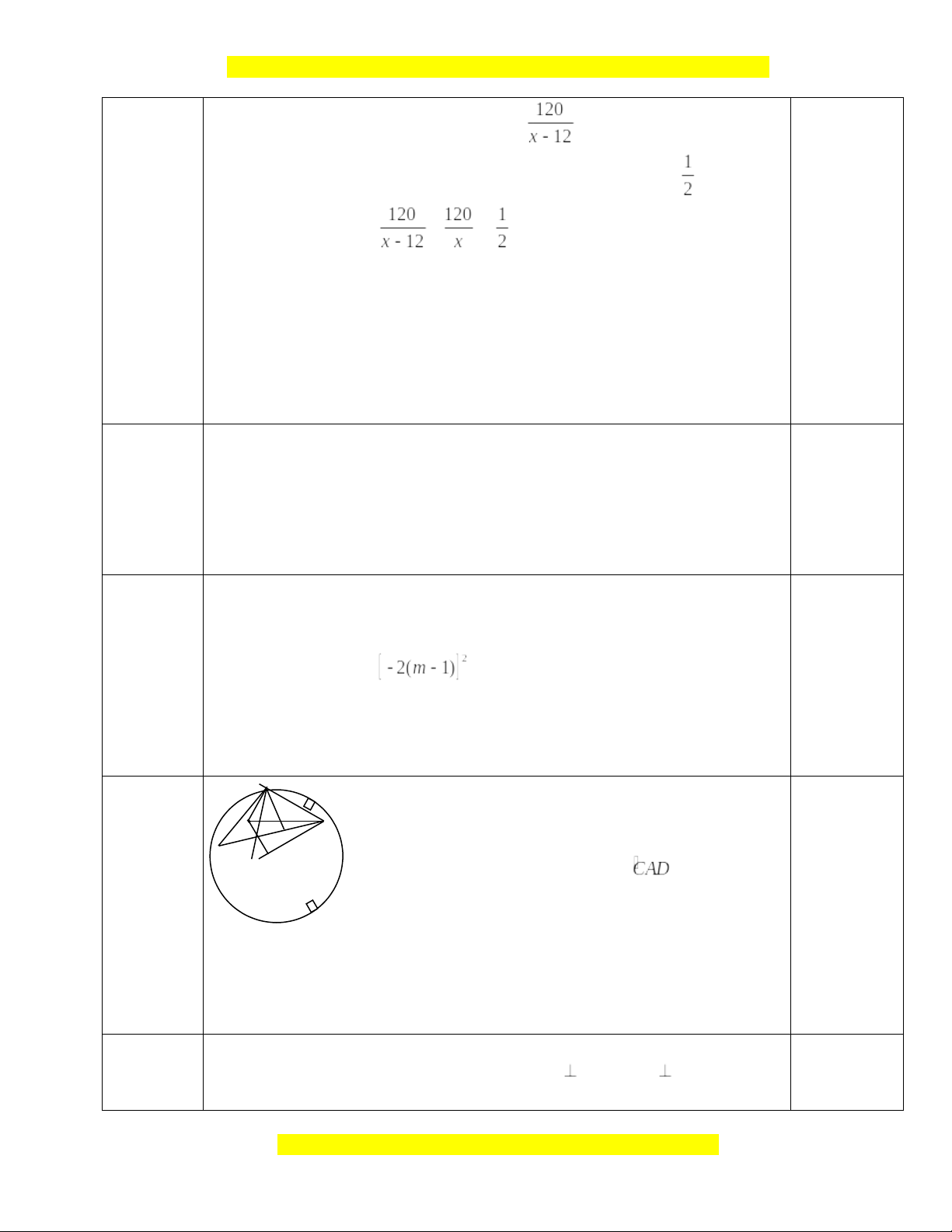
Phương trình có các hệ số : a = 1, b = 2b’=2(m-1), c = -m2 0,25 0,75đ
’ = (m-1)2 -1.(-m2) = (m-1)2 +m2 > 0, với mọi m . 0,25
Do đó phương trình đã cho luôn có hai nghiệm phân biệt. 0,25 Câu 4b
Theo hệ thức Viét : x1+ x2 = -2(m-1) ; x1x2 = -m2 0,5đ Ta có : x 2 2 1 + x2 = (x1+x2)2 –2x1x2 0,25 Suy ra : x 2 2 1 + x2 = -2.(-m2)= 4m2-8m+4 +2m2 0,25 = 6m2 -8m +4 0,25 A GT Cho (O ;R), M ngoài Câu 5 (O) ,OM=2R
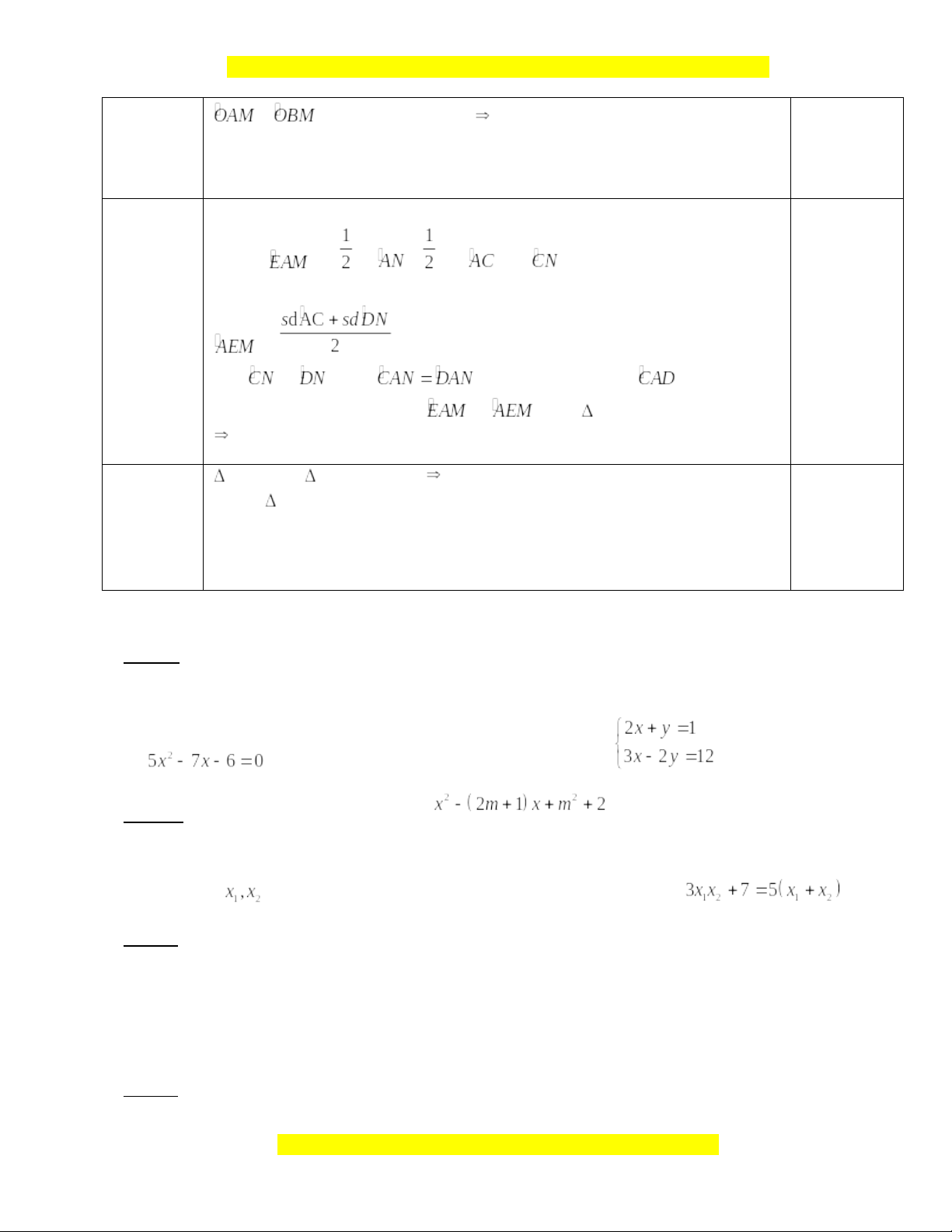
MA và MB là hai tiếp tuyến, MCD là O M cát C E tuyến, phân giác cắt CD tại E cắt (O) tại N. D B N
KL a).Chứng minh tứ giác OAMB nội tiếp được. b).Chứng minh MA = ME
c).Tính tích số MC.MD theo R. Câu 5a
Vì MA và MB là hai tiếp tuyến nên MA OA, MB OB nên 0,5 1đ
Document Outline
- Câu 5 ( 3,0 điểm)
- Cho đường tròn tâm O, đường kính BC, A là một điểm nằm trên đường tròn sao cho dây AB bé hơn dây AC. Trên đoạn OC lấy điểm D (D khác O, C). Từ D kẻ đường thẳng vuông góc với BC, đường thẳng này cắt hai đường thẳng BA và AC lần lượt tại E và F.
- Bài 1: (2,5 điểm)
- a) Cho phương trình: x2 + 6x + 5 = 0 có 2 nghiệm x1, x2.
- Không giải phương trình hãy tính: S = x1 + x2; P = x1. x2
- b) Giải hệ phương trình:
- c) Giải phương trình : x4 – 4x2 +3 = 0
- Bài 2: (1,5 điểm) Cho hàm số y = x2 có đồ thị là (P).
- a) Vẽ đồ thị (P) của hàm số.
- b) Tìm các điểm thuộc (P) có tung độ bằng -8.
- Bài 3: (2,0 điểm) Cho phương trình: x2 + 2mx + m + 2 = 0 (m là tham số)
- b) Tìm m để phương trình có nghiệm kép.
- Bài 4: (3,0 điểm) Cho đường tròn (O) đường kính BC. Từ điểm A ở ngoài đường tròn vẽ AB, AC lần lượt cắt đường tròn tại D và E sao cho số đo cung DE bằng 800. Gọi H là giao điểm của BE và CD.
- a) Tính  của ABC ?
- b) Chứng minh: Tứ giác ADHE nội tiếp.
- Bài 5: (1,0 điểm) Diện tích xung quanh của một hình trụ là 60 cm. Biết chiều cao của hình trụ này là h = 15 cm. Hãy tìm bán kính đường tròn đáy và thể tích của hình trụ đó.
- 1
- 1a
- S = x1 + x2 = -6; P = x1. x2 = 5
- 0,5 đ
- 1b
- Giải đúng nghiệm của hệ phương trình (x = 2, y = 1)
- 1,0 đ
- 1c
- Đặt t = x2 ( t 0) PT: t2 - 4t +3 = 0
- 0,25 đ
- 2
- 2a
- Vẽ đúng đồ thị (P)
- 1,0 đ
- 2b
- Tìm đúng các điểm thuộc (P): (-4; -8) và (4; -8)
- 0,5 đ
- 3
- 3a
- Khi m = – 1 ta có PT: x2 – 2x+1 = 0
- 0,5 đ
- 3b
- Tìm được ’ = m2 - m - 2
- PT có nghiệm kép khi ’ = 0 m2 - m - 2 = 0
- Tìm được m1 = -1, m2 = 2
- 0,25 đ
- 4
- 5
- Ta có: V = r2h = .22.15 = 60 (cm3)
- Bài 1: (2,5 điểm)
- a) Cho phương trình: x2 - 15x + 2 = 0 có 2 nghiệm x1, x2.
- Không giải phương trình hãy tính giá trị của biểu thức: A = x1 + x2 - 3x1.x2
- b) Giải hệ phương trình:
- c) Giải phương trình : x4 + 3x2 – 4 = 0
- Bài 2: (1,5 điểm) Cho hàm số y = ax2 có đồ thị là (P).
- a) Tìm a để đồ thị (P) đi qua điểm M(1; ).
- b) Vẽ đồ thị (P) với a vừa tìm được.
- Bài 3: (2,0 điểm) Cho phương trình: x2 + mx + m - 1 = 0 (m là tham số)
- b) Tìm m để phương trình có nghiệm kép. Tính nghiệm kép đó?
- Bài 4: (3,0 điểm) Cho ABC vuông tại A và ACB = 200. Trên cạnh AC lấy điểm D, vẽ đường tròn (O) đường kính CD cắt cạnh BC tại E. Đường thẳng BD cắt đường tròn (O) tại điểm thứ hai F.
- a) Tính số đo CDE ?
- b) Chứng minh tứ giác ABCF nội tiếp.
- c) Chứng minh BF là tia phân giác của góc AFE.
- Bài 5: (0,5 điểm) Diện tích xung quanh của một hình trụ là 120 cm. Biết chiều cao của hình trụ này là h = 15 cm. Hãy tìm bán kính đường tròn đáy của hình trụ đó.
- 1
- (2,5đ)
- 1a
- A = x1 + x2 - 3x1.x2 = 15 - 3.2 = 15 - 6 = 9
- 0,5 đ
- 1b
- Giải đúng nghiệm của hệ phương trình (x = 1; y = 3)
- 0,75 đ
- 1c
- Đặt t = x2 ( t 0) PT: t2 + 3t - 4 = 0
- 0,25 đ
- 2
- (1,5đ)
- 2a
- Tìm đúng a =
- 0,5 đ
- 2b
- Vẽ đúng đồ thị (P)
- 1,0 đ
- 3
- (2,0đ)
- 3a
- Khi m = 3 ta có PT: x2 + 3x + 2 = 0
- 0,25 đ
- 3b
- Tìm được = m2 - 4m + 4 = (m - 2)2
- PT có nghiệm kép khi = 0 (m - 2)2 = 0 m = 2
- Tính được nghiệm kép x1 = x2 = -1
- 0,5 đ
- 4
- (3,5đ)
- 0,5 đ
- a
- Lập luận: DEC = 900
- 0,5 đ
- b
- Lập luận: BAC = 900 và BFC = 900 Kết luận tứ giác ABCF nội tiếp.
- 0,5 đ
- c
- Lập luận đúng: BFE = BFA = ACB
- 0,5 đ
- 5
- I/ Lý thuyết : (4đ) Học sinh chọn ý đúng mỗi câu sau